1. Introduction
Recent studies in many species have found unexpectedly high frequencies of beneficial mutations. Shaw et al. (Reference Shaw, Geyer and Shaw2002) performed a mutation accumulation (MA) experiment in Arabidopsis thaliana and found that half of all mutations affecting fitness were beneficial. Garcia-Dorado (Reference Garcia-Dorado1997) re-analysed the fitness data from three Drosophila MA experiments and found that the results of one experiment were better fitted by a model incorporating 10% beneficial mutations than by a model assuming no beneficial mutations. Kassen & Bataillon (Reference Kassen and Bataillon2006) found that when spontaneous antibiotic mutations in Pseudomonas fluorescens were analysed in an environment lacking antibiotics, ~2–3% of non-neutral mutations were beneficial. Perfeito et al. (Reference Perfeito, Fernandes, Mota and Gordo2007) reported a rate of beneficial mutation in Escherichia coli that is three orders of magnitude higher than that estimated previously, with 1 in 10 mutations that affect fitness estimated to be beneficial. And in a previous MA study, we found that ~6% of mutations affecting yeast fitness were beneficial (Joseph & Hall, Reference Joseph and Hall2004).
While multiple studies have estimated high proportions of beneficial mutations, these estimates may be inaccurate due to the presence of natural selection or sampling error. Selection can cause overestimation of the true parameter by enriching for beneficial mutations. This bias can be corrected by a variety of methods. In this study and in a previous study, we used a correction based on work by Otto & Orive (Reference Otto and Orive1995) to downwardly adjust our initial estimate of the frequency of beneficial mutations (Joseph & Hall, Reference Joseph and Hall2004). Because estimates of this parameter are typically generated from studies that accumulate few mutations, they are prone to sampling inaccuracies that can lead to overestimation or underestimation of the true parameter value. Inaccuracies due to sampling error can be reduced by sampling more mutations.
Here, we investigate how sampling error affects estimates of the frequency of beneficial mutations by passaging our MA lines for an additional 1050 generations and re-estimating mutation parameters. The additional passages allow more mutations to accumulate, which should reduce the effect of sampling error. Surprisingly, our new estimate of the proportion of beneficial mutations, 13%, is actually two-fold higher than our previous one, though the confidence intervals are broadly overlapping. We conclude that while sampling error may influence parameter estimates in MA experiments, it does not explain our high estimates of the proportion of beneficial mutations. Our estimates, in conjunction with other reports, suggest that the true frequency of beneficial mutations is reasonably large, on the order of a few per cent.
We also update our previous estimates of mutation parameters in diploid yeast. We estimate that the genome-wide mutation rate for deleterious alleles is 8·8–76×10−5 mutations per haploid genome per cell generation, and the average absolute value of the heterozygous effect of a mutation is 7%.
2. Materials and methods
2.1. Experimental overview and ancestral strain
A detailed description of the MA procedure can be found in Joseph & Hall (Reference Joseph and Hall2004). Briefly, we established 152 genetically identical Saccharomyces cerevisiae lines from a diploid ancestor. The ancestor was derived from a haploid strain of genotype ade2, lys2–801, his3–Δ200, leu2–3·112, ura3–52, ho by transforming with an HO marker plasmid to induce diploidization, after which the plasmid was removed. The ancestor was thus homozygous at all loci except the mating-type locus, which was aα. The ade2 mutation was used to prevent the accumulation of mitochondrial petite mutations (Joseph & Hall, Reference Joseph and Hall2004), which has been a problem in previous yeast MA experiments (Korona, Reference Korona1999; Zeyl & DeVisser, Reference Zeyl and DeVisser2001). MA lines were propagated independently via single-cell transfer on YPD solid medium (1% yeast extract, 2% peptone, 2% dextrose and 2% agar) every 2 days for 200 days, for a total of 2062 cell generations. The non-competitive fitness of each line was measured relative to the ancestor by assaying growth in YPD liquid medium (see below) after 50 transfers (1012 generations; Joseph & Hall, Reference Joseph and Hall2004), and again after 100 transfers (2062 generations; this study). Fitness measures were used to generate maximum likelihood (ML) estimates of parameters of spontaneous mutations (Keightley, Reference Keightley1994; Keightley & Ohnishi, Reference Keightley and Ohnishi1998).
2.2. Generations of accumulation
We estimated the average number of generations per transfer from counts of the number of cells per colony, assuming exponential growth. The number of cells per colony was estimated approximately every seven transfers by choosing a single colony from each of the ten randomly chosen MA lines. We then suspended the colony in 1 ml of water and determined cell density using a haemocytometer (Reichert Bright Line, 0·1 mm depth).
2.3. Fitness assays
Our protocol for measuring fitness at transfer 100 is nearly the same as that used to measure fitness at transfer 50 (Joseph & Hall, Reference Joseph and Hall2004). The primary difference is that at transfer 100 we used 5 as opposed to 10 replicates per line and 20 as opposed to 50 ancestor replicates per plate (see below). The fitness of each MA line was estimated by comparing its maximum growth rate to that of the ancestor. Maximum growth rates were estimated from optical density measurements obtained using a Bioscreen C Microbiological Workstation (Thermo Labsystems).
We began fitness assays by streaking samples of each MA line and the ancestor from the freezer onto solid YPD medium and letting them grow for 2 days. We then inoculated replicate, overnight, liquid cultures from individual colonies growing on the solid medium. The next morning we transferred 40 μl of each overnight culture into 2 ml of fresh liquid YPD. These cultures were allowed to grow for 6 h, at which time they were in the logarithmic growth phase, and then a 150 μl aliquot was added to 2 ml of fresh YPD. A 150 μl sample of the resulting culture was immediately loaded into a microplate well. Two microplates, each containing 100 wells, were then placed in a Bioscreen C microbiological workstation (Thermo Labsystems), which incubated them at 30°C with continuous, intense shaking and recorded the absorbance of 600 nm light for each well every 10 min for 46 h. Absorbance readings were log-transformed and used to generate growth curves (log absorbance vs. time).
Growth curves were used to estimate the fitness of each MA line. For every growth curve, a least squares regression of log absorbance on time was calculated for a sliding 120 min window. Maximum growth rate was calculated as the largest slope of the regressions. The maximum growth rate of each line replicate was standardized by dividing by the mean maximum growth rate of the 20 ancestor replicates on the same microplate. The standardized maximum growth rate of a replicate was designated as the fitness of that replicate and the average fitness of the five replicates of each line was designated as the fitness of the line. Each ancestor replicate was standardized in the same manner. Thirty-three lines initially had one or more replicates that could not be used because of growth anomalies. We repeated the fitness assay for each of these lines.
2.4. General statistical analysis
Statistical tests were performed using JMP statistical software (version 6.0, SAS Institute, Cary, NC). We estimated the per-generation mutational increase in genetic variance in fitness, σm2, as half the among-line variance, determined using ANOVA, divided by the number of generations (Schultz et al., Reference Schultz, Lynch and Willis1999). We calculated the mutational heritability for fitness, h m2, as the per-generation mutational variance divided by the within-line (environmental) variance (Falconer & Mackay, Reference Falconer and MacKay1996). We also determined the mutational coefficient of variation, CVm, as the square root of the mutational variance divided by the mean and multiplied by 100 (Houle et al., Reference Houle, Morikawa and Lynch1996).
The number of MA lines that were significantly different from the ancestor was determined with a Kruskal–Wallis test. We used this test because the fitness distributions of the MA lines and ancestor replicates were not normally distributed (P<0·01 for the ancestor and P<0·00001 for the MA line distributions, Shapiro–Wilks W) and their variances were unequal (Levene's test, P<0·0001). Corrections for multiple comparisons were performed using both sequential-Bonferroni correction (Rice, Reference Rice1989) and a method introduced by Benjamini & Hochberg (Reference Benjamini and Hochberg1995). Sequential-Bonferroni correction (Rice, Reference Rice1989) minimizes the probability of Type 1 error (false discovery rate or false positives) and can result in many Type 2 errors (false negatives) as the number of comparisons increases (Verhoeven et al., Reference Verhoeven, Simonsen and McIntyre2005). The Benjamini–Hochberg correction maintains a relatively constant probability of Type 1 error as the number of comparisons increases, thus reducing the number of Type 2 errors.
2.5. Fitness at transfers 50 and 100
MA lines that accumulated mutations prior to transfer 50 should still show the effects of those mutations at transfer 100, and we thus expect a significant correlation between fitness at transfer 100 and fitness at transfer 50. Since half of the mutations present at transfer 100 are expected to have arisen since transfer 50, we expect the correlation to be 0·5 in the absence of epistasis and beneficial mutations. In order to determine the correlation between fitness measures at transfers 50 and 100, we fitted our data with a mixed linear model using restricted ML, with the MIXED procedure in the SAS software package (version 8.0, SAS Institute). The mixed linear model allows among-line and within-line variances in fitness to differ between the two transfers (using TYPE=UNR), thus giving an unbiased estimate of the correlation (Fry, Reference Fry and Saxton2004b). We also tested whether the correlation was significantly different from 1 and 0·5 using the appropriate PARMS statements.
2.6. Estimates of mutational parameters
As in our previous study, we used log likelihood to estimate the proportion of mutations that are beneficial (P), the genome-wide mutation rate for alleles that alter fitness (U) and the absolute value of the mean heterozygous fitness effect of mutations (E(hs)). The ML estimates were calculated using a program provided by Dr Peter Keightley (Keightley, Reference Keightley1994; Keightley & Ohnishi, Reference Keightley and Ohnishi1998). The program estimates mutation parameters from the fitness values of the MA lines and the ancestor. The program assumes that the number of mutations accumulated in each MA line is Poisson-distributed and that the effects of mutations follow a reflected gamma distribution with a fraction P of the mutations having positive (beneficial) effects. The positive and negative parts of the distribution are assumed to have the same scale parameter α and shape parameter β. The mean heterozygous fitness effect, E(hs), is equal to β/α.
MA line fitness was used instead of replicate fitness in the likelihood analysis to avoid excessive computer time by reducing the size of the data set. In addition, the mean fitness of groups of five ancestor replicates was used. The reduced data consisted of 149 MA line fitness measures (three lines did not regrow from the freezer, see below) and 46 ancestor fitness measures.
With the reduced data set, we performed a search of the parameter space by first choosing values of β and P and then running the program to find the ML values of α and U. After narrowing in on the region of the parameter space in which estimates of β, P, α and U showed high likelihoods, we performed additional runs of the program in those regions to obtain more accurate estimates of the ML values of the parameters and their 95% confidence intervals. Additionally, we ran an equal effects model for all values of P. Finally, we repeated these analyses on the data after removing an MA line carrying a very large-effect deleterious mutation.
We also estimated the mutation rate and average effect using the Bateman–Mukai approach (Bateman, Reference Bateman1959; Mukai, Reference Mukai1964). With this approach, the change in the mean fitness across all MA lines and the among-line variance are used to generate parameter estimates, but beneficial mutations are not considered. In addition, variance in mutational effects causes this method to underestimate the genome-wide mutation rate and overestimate the average effect of mutations (Lynch et al., Reference Lynch, Blanchard, Houle, Kibota, Schultz, Vassilieva and Willis1999).
2.7. Correction for selection
The number of mutations accumulated during the experiment is affected by selection during colony growth. Our experimental design attempted to minimize the efficacy of selection by maintaining a small effective population size. Even so, deleterious and beneficial mutations are expected to be under- and over-represented in the MA lines relative to their occurrence. This is a problem common to all MA experiments and results in biased estimates of the parameters of mutation. We utilized a method developed by Otto & Orive (Reference Otto and Orive1995) to correct our parameter estimates. They derived equations to calculate the number of new-mutant and non-mutant cells in an individual, starting from a single cell. Their equations are exactly applicable to within-colony selection. The number of mutant cells of effect hs, M hs, present in a colony after n generations of growth is
The probability, P hs, that a mutation with effect hs will be fixed during a transfer is equal to its frequency in the colony at the end of colony growth. It is given by
To calculate the bias in the probability of fixation caused by selection for a mutation of a given effect, we simply calculate the probability of fixation for that mutation relative to the probability of fixation for a neutral mutation, with effect equal to 0. This gives the relative probability of fixation of a mutation as
Deleterious mutations (hs<0) will have relative fixation probabilities that are less than 1 and beneficial mutations (hs>0) will have relative fixation probabilities greater than 1.
We used eqn (3) to calculate the bias caused by selection, assuming different mutation rates, as a function of the effect of mutation. We then used the bias calculations to correct our estimates of the proportion of mutations that were beneficial. The corrections were done using Mathematica (version 5.2, Wolfram Research, Inc., Champaign, IL).
3. Results
3.1. Generations and effective population size
For 98 of the 100 transfers, the average colony size was estimated to be 1·7×106 cells, which represents approximately 20·7 generations between transfers, or one cell division every 139 min. For transfers 23 and 24, the colony size was much smaller, 0·11×106 cells, representing approximately 16·7 generations between transfers. Due to lab error, the medium for these two transfers had a different peptone source, which accounts for the less vigorous growth. Combining these estimates, transfers occurred every 20·6 generations and the MA period was 2062 generations. The harmonic mean population size of our MA lines, which serves as an estimate of the effective population size, is 10·8 cells per line. There was no trend towards reduced colony size in the MA lines over the course of the experiment.
3.2. Fitness distributions
Only 149 out of the 152 MA lines could be regrown from the freezer, so fitness could only be measured on these lines. In our previous study, one line did not regrow from the freezer, and we assumed that we had inadvertently skipped it when freezing transfer 50. That line again failed to regrow during this study, as did two additional lines. All three of these lines had cells in their freezer stock, indicating that they had been frozen. We conclude that these lines had accumulated mutations that made them sensitive to freezing.
The fitness distributions of the remaining 149 MA lines and ancestors at transfer 100 are plotted in Fig. 1 B, and the distributions at transfer 50 are shown in Fig. 1 A for comparison. Using sequential Bonferroni to correct for multiple comparisons (Rice, Reference Rice1989), a Kruskal–Wallis test indicated that eight lines were significantly different from the ancestor (α=0·05). All eight had lower fitness than the ancestor. Using the Benjamini–Hochberg procedure to correct for multiple comparisons (Benjamini & Hochberg, Reference Benjamini and Hochberg1995), 36 lines were significantly different from the ancestor, of which 10 (28%) had higher fitness (Table 1).

Fig. 1. Fitness distributions of ancestor groups and MA lines at transfer 50 (A) and transfer 100 (B). At transfer 50, there are 151 MA lines and 151 ancestor fitness values shown, and each is the mean of ten replicates (data from Joseph & Hall, Reference Joseph and Hall2004). At transfer 100, there are 149 MA lines and 46 ancestor fitness values, each representing the mean of five replicates.
Table 1. The number of MA lines that are significantly different at the 5% level using either sequential Bonferroni correction (Rice, Reference Rice1989) or a method introduced by Benjamini & Hochberg (Reference Benjamini and Hochberg1995) to correct for multiple comparisons (see text for details)

The summary statistics for the MA line and ancestor distributions are shown in Table 2. Over the 2062 generations of MA, the MA lines experienced a significant decline in mean fitness (Kruskal–Wallis, P<0·0001) and increase in variance (Levene's test, P<0·0001). Further, the mean fitness of the MA lines at transfer 100 is significantly smaller than the fitness at transfer 50 (Kruskal–Wallis, P<0·0001). The partitioning of variance using ANOVA allowed us to calculate the within- and between-line variances. Between-line variance is higher at transfer 100, resulting in a higher estimate of mutational variance. In spite of higher mutational variance, heritability decreased because environmental variance, captured as within-line variance, also increased between transfers 50 and 100. Some of the increase in mutational variance is due to one extremely sick line, with a mean fitness of 0·55. Removal of this line reduces the estimate of between-line variance by 30%, with a concomitant decline in heritability (Table 2). Despite the fitness measures from transfer 100 having a higher variance and lower mean than at transfer 50, their coefficient of variation in fitness is quite similar.
Table 2. Summary statistics of the distributions of MA lines and ancestor, and estimates of per-generation mutational increase in genetic variance in fitness, σm2, mutational heritability for fitness, hm2, and the mutational coefficient of variation, CVm, at transfer 50 (T50) and transfer 100 (T100). Data for transfer 50 are from Joseph & Hall (Reference Joseph and Hall2004)

a 1510 replicates at transfer 50 and 238 replicates at transfer 100.
b Estimate with the one extremely sick line removed.
c Heritability was incorrectly reported as 1·1×10−3 in Joseph & Hall (Reference Joseph and Hall2004).
The ancestor variance and the MA within-line variance were both ~3·5 times larger at transfer 100 than at transfer 50 (Table 2). We are unable to explain why these estimates of error variance were greater at transfer 100 than at transfer 50. The manufacturers of the media ingredients assured us that there was no change in the composition of the ingredients, though we noticed a change in the consistency of the bacto-peptone (Difco brand). Alternatively, the 3 years spent in the −80°C freezer before the transfer 100 fitness assays may have increased the error variance in the growth rate of the stored MA lines and ancestor, perhaps due to physiological changes that were passed through several cell generations after thawing.
3.3. Fitness at transfers 50 and 100
The MIXED procedure gave a significant correlation (P<0·0001) between fitness at transfer 100 and fitness at transfer 50. The correlation coefficient is 0·38 with a standard error of 0·08, and is significantly different from 1 (P<0·0001), but not from 0·5 (P=0·13). This is consistent with the predicted slope of less than one, indicating that the lines accumulated additional mutations during the last 50 transfers that were, on average, deleterious. For illustration purposes, we plot the fitness at transfer 100 against transfer 50 for each of the 149 MA lines in Fig. 2.

Fig. 2. Relationship between fitness at transfer 50 (1012 cell generations) and fitness at transfer 100 (2062 cell generations) for 149 MA lines.
3.4. Estimates of mutational parameters
Bateman–Mukai estimates are shown in Table 3. There is good agreement between estimates at transfer 50 and estimates at transfer 100, especially when the one line exhibiting very low fitness is removed.
Table 3. (A) ML estimates (and 95% confidence intervals) of the genome-wide, haploid mutation rate (U), the absolute value of the average effect of a mutation (E(hs)) and the proportion of mutations that are beneficial (P) at transfer 50 (151 MA lines) and transfer 100 (149 MA lines). In the last two columns, separate estimates for the genome-wide, haploid mutation rate and the average effect of beneficial and deleterious mutations for transfer 100 are shown. Transfer 50 estimates are from Joseph & Hall (Reference Joseph and Hall2004). Corrected estimates of the parameters, indicated by an asterisk (*), were generated by performing the Otto & Orive (Reference Perfeito, Fernandes, Mota and Gordo1995) correction for the effects of natural selection during colony growth (see text). (B) Bateman–Mukai estimates of the genome-wide, haploid mutation rate (U) and the absolute value of the average effect of a mutation (E(hs))
(A) ML
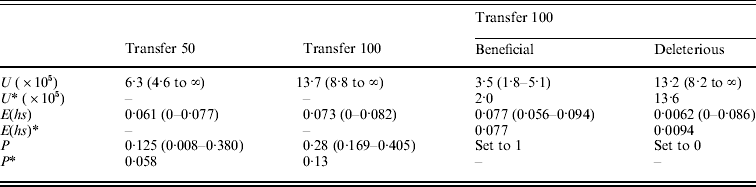
(B) Bateman–Mukai

Results from the likelihood analysis are shown in Fig. 3. The ML estimates (and 95% confidence intervals) are: proportion of beneficial mutations, P=0·28 (0·169–0·405); the absolute value of the average effect, E(hs)=0·073 (0–0·082); and the genome-wide, haploid mutation rate, U=13·7×10−5 (8·8×10−5 to ∞). The equal effects model gave the highest likelihood. Several other distributions, including the exponential, give likelihoods within two log units of the maximum. Examples of such distributions are shown in Fig. 4.

Fig. 3. Profile log likelihood curves as a function of mutational parameters for the analysis of the complete data set for transfer 100. (A) The absolute value of the average effect of a mutation, E(hs). (B) The genome-wide, haploid mutation rate for alleles that alter fitness, U. (C) The proportion of mutations accumulated that were beneficial, P. The reported estimates for each parameter in the text are those values that give the MLover all combinations of β and P. To obtain 95% confidence intervals around these estimates, the curves are extrapolated to determine the parameter values at which there is a two-log-unit reduction in likelihood.

Fig. 4. Distributions of the absolute value of the heterozygous effect of a mutation. The ML was obtained with an equal effects model and appears as a vertical line at 0·073. The other distributions represent the range of effect distributions that are consistent with the data: that is, their fit of the data is not significantly different from that of the equal effects model.
3.5. Correcting parameter estimates for selection
Figure 5 illustrates the bias in fixation probability generated by selection during colony growth, which is calculated using eqn (3), as a function of the effect of a mutation. Two points are apparent from the relationship. First, the effect of selection during colony growth on relative fixation probability is insensitive to variation in the mutation rate: the three curves for U=10−3, 10−4 and 10−5 cannot be distinguished. Secondly, selection causes biases that are less than two-fold, such that beneficial mutations are less than twice as common as expected and deleterious mutations are at least half as common as expected, for mutations with an absolute effect of ~0·1 or smaller. It is only for mutations of large absolute effect, greater than 0·1, that bias becomes large.

Fig. 5. Relative probability of fixation as a function of effect of mutation. The relative probability of fixation is calculated as the probability that a selected mutation arising in an MA line will be fixed in that line relative to the probability of fixation for a neutral mutation. Selection during colony growth biases the fixation probability, causing deleterious mutations (with negative fitness effect) to be under-represented and beneficial mutations to be over-represented. As previously shown by Kibota & Lynch (Reference Kibota and Lynch1996), the bias in fixation probability is insensitive to mutation rate.
The bias curve can be utilized to correct estimates of the average effect and proportion of mutations that are beneficial (Table 4). The ML estimate of the effect distribution was an equal effects model, in which all mutants have the same effect, and so no correction was needed for the average effect, which thus remained the same at 0·073. The relative frequency of beneficial and deleterious mutations does require correction. With an absolute value of average effect of 0·073, deleterious mutations are under-represented by ~35% and beneficial mutations are over-represented by ~70%. We used these percentages to adjust the relative frequency of deleterious and beneficial mutations (reducing the frequency of beneficials and increasing the frequency of deleterious). Using this method, the corrected frequency of beneficial mutations is 13%.
Table 4. Some estimates of haploid mutation rates, effects of mutations and mutational heritability from several MA experiments. The effect of mutations is measured in homozygotes, except where noted. LRS, lifetime reproductive success; MGR, maximum growth rate; r, growth rate. Table modified from Bataillon (2000)

a Mean effect in heterozygotes.
b Mean effect in haploids.
c Data from a mutator line.
4. Discussion
The primary goal of this study was to update our earlier estimates of mutational parameters, especially the frequency of mutations affecting fitness that are beneficial, and assess the role of sampling error in our MA experiment. In this section, we present the updated estimates of yeast mutational parameters and discuss the implications of the estimated values. In particular, we again find a high frequency of beneficial mutations.
4.1. Proportion of mutations affecting fitness that are beneficial
The uncorrected and corrected ML estimates (P=0·28 and 0·13) indicate that beneficial mutations are relatively common in our yeast strain. This is in agreement with our previous estimates (P=0·13 and 0·06; Joseph & Hall, Reference Joseph and Hall2004). There are at least four possible explanations.
First, the beneficial mutation rate may have been elevated – because the ancestral strain had low fitness – and thus was far from the optimal phenotype. This is predicted by Fisher's geometric model of adaptation, which states that the further a genotype lies from the optimal phenotype, the more likely that a mutation is beneficial (Fisher, Reference Fisher1930). This is also consistent with the observation that low fitness yeast adapts more rapidly than high fitness yeast (Joseph & Kirkpatrick, Reference Joseph and Kirkpatrick2008). The fitness of our ancestral strain may have been reduced by mutations that it carries in five biosynthetic pathways. One of those mutations, ade2, has previously been shown to reduce maximum growth rate (Ugolini & Bruschi, 1996, and personal observation). In addition, our lab strain has not been adapted to the fitness assay environment. It is thus quite possible that our starting strain is far from the optimal phenotype, implying that a relatively high frequency of mutations affecting fitness will be beneficial.
Secondly, we may have accumulated mutations that are deleterious or neutral in some environments but beneficial in our fitness assay environment. We measured fitness in complete medium (YPD) at 30°C. Complete medium at 30°C is a relatively benign environment, supporting the growth of essentially all non-lethal genotypes. It has been shown that mutational effects, including effects on growth rate, tend to be more deleterious in a more stressful environment (Szafraniec et al., Reference Szafraniec, Borts and Korona2001). We have assayed the fitness of the transfer-50 MA lines in four other environments, and we find that beneficial mutations are environment-specific (unpublished data). However, even in minimal environments we find a high frequency of beneficial mutations (unpublished data), indicating that the complete medium used in our fitness assay is not the only explanation for the high frequency of beneficial mutations observed.
Thirdly, the effects of mutations may differ across different stages of the life cycle. We only measured one component of fitness, diploid growth rate. We chose this measure because, as a homothallic fungus, diploidy is the usual ploidy level for yeast, and growth rate is thought to be an important component of fitness in microbes (Table 4). There are several other fitness components that could have been examined, including sporulation efficiency, haploid growth rate, mating efficiency and (diploid or haploid) competitive growth rate. If we had used a fitness measure that incorporated all components of the yeast sexual cycle, it is possible that we would have found no evidence for beneficial mutations. We are currently investigating this possibility.
Fourthly, dominance may upwardly bias our estimates of the frequency of beneficial mutations. In many MA experiments, mutations are scored in haploids or in homozygous diploids. In our experiment, in which mutations arise in an asexual diploid, accumulated mutations are heterozygous. If deleterious mutations tend to be more recessive than beneficial mutations, we will score a higher proportion of the beneficial than the deleterious mutations. The average dominance coefficient of random deleterious mutations in yeast has been estimated as 0·197 (Szafraniec et al., Reference Szafraniec, Wloch, Sliwa, Borts and Korona2003). We know of no estimate for the dominance coefficient of random beneficial mutations. Overdominance will also upwardly bias our estimate of the beneficial mutation rate. In our experiment, overdominant mutations will be scored as beneficial because we are scoring heterozygotes. The same mutations, scored in homozygotes, might very well be deleterious. Peters et al. (Reference Peters, Halligan, Whitlock and Keightley2003) found that 3 of 19 crosses between unmutated and mutated lines showed evidence of overdominance in Caenorhabditis elegans, suggesting that overdominant mutations might be quite common. Fry (Reference Fry2004c) has argued that this pattern is also consistent with mutant lines containing both recessive deleterious and partially dominant beneficial mutations in the lines. If Fry's explanation is the reason for apparent overdominance, it suggests that beneficial mutations tend to have higher dominance, bolstering the previous hypothesis concerning upward bias due to dominance.
Regardless of the specific explanation, it is clear that the frequency of beneficial mutations for diploid growth rate in complete medium is high in our strain. This implies that our strain should be able to readily adapt to the fitness assay environment. These data, coupled with data from other species (see section 1), suggest that adaptation is unlikely to be limited by mutation rate in populations of reasonable size. In addition, the loss of small populations due to genetic load will also be mitigated by high frequencies of beneficial mutations (Whitlock et al., Reference Whitlock, Griswold and Peters2003).
4.2. Distribution of mutational effects
Our ML estimate of the distribution of mutational effects is one in which all mutations have the same average effect; however, the broad confidence intervals around the ML estimate reveal that a wide variety of distributions fit the data (Fig. 4). The inability to distinguish among these distributions is discouraging, because the shape of the distribution has important implications for a variety of evolutionary phenomena. For example, small-effect deleterious mutations are more likely to go to fixation through drift (Whitlock, Reference Whitlock2000) and, in non-recombining regions of a genome, cause Muller's ratchet to proceed more quickly (Gordo & Charlesworth, Reference Gordo and Charlesworth2000). Such small-effect deleterious mutations are common in distributions that are L-shaped, and are essentially absent in distributions with narrow peaks centred away from zero (Fig. 4). Both types of distributions are consistent with our data.
The wide variety of the distributions consistent with our data may be caused by two factors. First, the fitness change measured in an MA line is caused by the accumulation of mutation(s) with particular effects. As such, we are measuring a fitness effect caused by a product of two parameters: mutation rate and mutational effect. However, we are attempting to estimate each parameter separately. It is perhaps not surprising that distinguishing many mutations of small effect from a few mutations of intermediate effect is difficult. Secondly, it is possible that one or more of the assumptions of the likelihood program are violated. It would be interesting to examine how well the ML program estimates parameters when particular assumptions are violated. One obvious assumption to examine is the reflected gamma effect distribution for deleterious and beneficial mutations. If beneficial and deleterious mutations have substantially different effect distributions and beneficial mutations are relatively frequent, then the likelihood program may be unable to distinguish among various distributions. Addressing these questions requires a simulation study. Unfortunately, the ML program is computer-time-intensive when beneficial mutations are present (P≠0), and so a full assessment is beyond the scope of this study.
4.3. Genome-wide mutation rate
The ML estimate of the genome-wide mutation rate for alleles that alter fitness, based on the likelihood analysis of all MA lines, is consistent with previous estimates from yeast (Table 4), though the confidence intervals are extremely broad. We are able to use the yeast, per base pair, mutation rate to put an upper bound on our confidence interval. Drake et al. (Reference Drake, Charlesworth, Charlesworth and Crow1998) reported that the haploid, genome-wide, base pair mutation rate in yeast, extrapolating from the per base pair mutation rate, is 0·0027. Given that ~72% of the yeast genome encodes genes (Sherman, Reference Sherman2002), and assuming that at most approximately 3/4 of the mutations in such genes cause an amino acid substitution (Li, Reference Li1997) or regulatory change in the gene, and could thus be selected, we obtain an upper limit to the haploid, genome-wide mutation rate for alleles that alter fitness of ~0·00146. This upper limit greatly narrows the confidence intervals of our mutation rate estimate. The Drake et al. estimate is based on 23 fluctuation tests performed on two loci (Drake, Reference Drake1991). Extrapolating from two loci to the entire genome is a little unsettling, but no other estimate has been reported. Keeping the possible weaknesses of our upper limit in mind, we conclude that the genome-wide mutation rate for deleterious alleles is between 8·8×10−5 and 146×10−5 mutations per haploid genome per cell generation. The lower value is close to the lowest previous estimate in yeast, 4·8×10−5 (Zeyl & DeVisser, Reference Zeyl and DeVisser2001), and the upper value is almost three times larger than the highest previous estimate, 55×10−5 (Wloch et al., Reference Wloch, Szafraniec, Borts and Korona2001). Placing an upper limit on the genome-wide mutation rate for alleles that alter fitness also places a lower limit on the average effect of a deleterious mutation of ~0·004 for our experiment.
The lower mutation rate observed for yeast, relative to other eukaryotes (Table 4), is likely to be an artefact of measuring the mutation rate per cell generation and due to a large proportion of mutations in yeast behaving neutrally. In multicellular eukaryotes, the germline goes through several cell generations per organism generation, and thus the per generation mutation rate includes several cell generations. For example, Drosophila melanogaster has approximately 36 cell divisions in the germline per generation (Drost & Lee, Reference Drost and Lee1995) and the mutation rate for alleles that alter fitness per cell division is about 0·005 (Lynch et al., Reference Lynch, Blanchard, Houle, Kibota, Schultz, Vassilieva and Willis1999). This value is higher than the value we see in microbes, even though the number of base pair substitutions per cell division is similar (Drake, Reference Drake1991; Drake et al., Reference Drake, Charlesworth, Charlesworth and Crow1998). The low genome-wide mutation rate for alleles that alter fitness may also be explained by the fact that yeast has numerous genes that can be mutated without causing a fitness effect, at least in the rich media used in MA experiments (Winzeler et al., Reference Winzeler, Shoemaker, Astromoff, Liang, Anderson, Andre, Bangham, Benito, Boeke, Bussey, Chu, Connelly, Davis, Dietrich, Dow, El Bakkoury, Foury, Friend, Gentalen, Giaever, Hegemann, Jones, Laub, Liao, Liebundguth, Lockhart, Lucau-Danila, Lussier, M'Rabet, Menard, Mittmann, Pai, Rebischung, Revuelta, Riles, Roberts, Ross-MacDonald, Scherens, Snyder, Sookhai-Mahadeo, Storms, Véronneau, Voet, Volckaert, Ward, Wysocki, Yen, Yu, Zimmermann, Philippsen, Johnston and Davis1999). Szafraniec et al. (Reference Szafraniec, Borts and Korona2001) have shown that stressful environments expose many mutations that have no effect on fitness in a rich environment, which would increase mutation rate estimates and estimates of mutational heritability.
4.4. Mutational heritability, hm2
The estimates of mutational variance in our MA lines at transfer 100 were standardized to yield mutational heritabilities (h m2) of 2·4 or 3·3×10−4, depending on whether the MA line with the lowest fitness was excluded. These estimates are smaller than those obtained at transfer 50, which can be attributed to the increase in error variance of our fitness measure at transfer 100. Our estimates are of similar magnitude to the only other estimate in diploid yeast, 4·8×10−4 (Zeyl & DeVisser, Reference Zeyl and DeVisser2001), but smaller than the mutational heritabilities seen in many eukaryotes (Lynch, Reference Lynch1988). This can be attributed to the low genome-wide mutation rate in yeast.
4.5. Transfer 50 versus transfer 100 parameter estimates
A goal of this study was to determine whether sampling error influences parameters estimated from MA experiments. Of particular interest is whether sampling error can explain the unexpectedly large proportion of beneficial mutations that we observed in a previous study (Joseph & Hall, Reference Joseph and Hall2004). In order to address this, we compared parameters estimated at transfer 50 (our previous study) to parameter estimates made after 100 transfers (this study).
Our analysis of the MA lines after 100 transfers makes it clear that sampling error can cause differences in parameter estimates, but that it cannot explain the large proportion of beneficial mutations observed in our MA lines. The uncorrected and corrected ML estimates of P from transfer 100 (P=0·28 and 0·13) are two-fold larger than the estimates from transfer 50 (P=0·125 and 0·058). While the difference between these estimates is sizeable, their confidence intervals are large and overlap substantially (Table 4), so that we cannot reject the hypothesis that the proportion of mutations accumulated in the MA lines was the same at both transfers.
We can also address the importance of sampling for the other estimated parameters. There was a two-fold difference in the genome-wide mutation rate estimates from the likelihood analysis involving all MA lines, but again the confidence intervals show substantial overlap. The transfer 100 ML estimate of the mutation rate is a good fit to the data from transfer 50 (likelihood ratio test, P>0·1), though the reverse is not true (likelihood ratio test, P<0·0005). The estimates of the average effect are almost identical at transfers 50 and 100 (Table 3), implying that this parameter was not affected by sampling error.
Besides sampling error, there is at least one alternative explanation for the increase in our estimate of the genome-wide mutation rate at transfer 100 compared to transfer 50. As the number of accumulated mutations increases, multiple deleterious mutations in the same MA line might exhibit synergistic epistasis, such that later hits are more easily detected, which would cause our estimate of mutation rate at transfer 100 to be larger than that at transfer 50. In D. melanogaster, a re-analysis of previous experiments revealed accelerating declines in fitness during MA, consistent with synergistic epistasis (Fry, Reference Fry2004a). In C. elegans, ML estimates of genome-wide mutation rate tended to increase with the generation assayed (Vassilieva et al., Reference Vassilieva, Hook and Lynch2000), also supporting synergistic epistasis. Based on our ML estimate of the genome-wide mutation rate, we estimate that ~86 mutations accumulated during the ML experiment. Assuming that these mutations are independent, the probability that two or more mutations occur within a line is 0·11, implying that 16 lines accumulated two or more mutations. With only 16 of 152 lines predicted to carry two or more mutations, the opportunity for synergistic epistasis is limited. If the mutation rate is actually closer to the upper limit of our mutation rate confidence interval (146×10−5), then each line would have accumulated ~6 mutations, giving ample opportunity for synergism. Synergistic epistasis is expected to increase the effect of later mutations, resulting in an increase in the estimate of average effect from later generations of MA. We did not observe such an increase. Given the limited opportunity, and no increase in average effect, we believe that synergistic epistasis is unlikely to explain our increased estimate of mutation rate.
Our finding of a significant correlation between MA line fitness at transfer 50 and at transfer 100, with a slope less than one, indicates that MA lines continued to accumulate mutations that were, on average, deleterious. Correlations between fitness values for individual MA lines are not reported in the literature, and so we are unable to compare the value of our regression to previous work. Keightley & Bataillon (Reference Keightley and Bataillon2000) graph the rank order of MA lines at two different generations of MA (Fig. 2 in Keightley & Bataillon, Reference Keightley and Bataillon2000, data from Vassilieva & Lynch, Reference Vassilieva and Lynch1999), though they do not report the Spearman correlation coefficient. The relationship between rank order at transfers 50 and 100 shows similar scatter in our data, though the Spearman correlation is significant (data not shown, ρ=0·2379, P=0·0035).
In summary, we have updated our previous mutation parameters and have shown that sampling error may be responsible for altering our parameter estimates as much as two-fold, which is comparable to the variation observed in MA experiments started with different nematode genotypes (Baer et al., Reference Baer, Shaw, Steding, Baumgartner, Hawkins, Houppert, Mason, Reed, Simonelic, Woodard and Lynch2005). However, our previous finding of a high proportion of mutations that affect fitness being beneficial does not seem to be due to sampling error. Instead, the high estimate may be due to a maladapted ancestral genotype, the benign environment in which we assayed fitness, the consideration of only one component of fitness, or differences in dominance coefficients between deleterious and beneficial mutations. Distinguishing among these alternatives will require additional experimentation.
We thank the anonymous reviewers for helpful comments. This study was supported in part by National Science Foundation grant DEB–09973221 (to Mark Kirkpatrick), by National Science Foundation dissertation improvement grant DEB–0309372 (S.B.J.) and by The University of Georgia at Athens (D.W.H.).










