Hostname: page-component-cb9f654ff-c75p9 Total loading time: 0 Render date: 2025-08-04T09:59:18.623Z Has data issue: false hasContentIssue false
  • English
  • Français

BGG CATEGORY FOR THE QUANTUM SCHRÖDINGER ALGEBRA

Part of: Lie algebras and Lie superalgebras Linear algebraic groups and related topics

Published online by Cambridge University Press:  20 April 2020

GENQIANG LIU  and
YANG LI
GENQIANG LIU
Affiliation:
School of Mathematics and Statistics, Henan University, Kaifeng 475004, P.R. China, e-mails: liugenqiangbnu@126.com; 897981524@qq.com
YANG LI
Affiliation:
School of Mathematics and Statistics, Henan University, Kaifeng 475004, P.R. China, e-mails: liugenqiangbnu@126.com; 897981524@qq.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1996, a q-deformation of the universal enveloping algebra of the Schrödinger Lie algebra was introduced in Dobrev et al. [J. Phys. A 29 (1996) 5909–5918.]. This algebra is called the quantum Schrödinger algebra. In this paper, we study the Bernstein-Gelfand-Gelfand (BGG) category 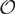$\mathcal{O}$ for the quantum Schrödinger algebra 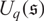$U_q(\mathfrak{s})$, where q is a nonzero complex number which is not a root of unity. If the central charge 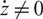$\dot z\neq 0$, using the module 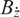$B_{\dot z}$ over the quantum Weyl algebra 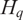$H_q$, we show that there is an equivalence between the full subcategory 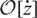$\mathcal{O}[\dot Z]$ consisting of modules with the central charge 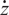$\dot z$ and the BGG category 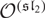$\mathcal{O}^{(\mathfrak{sl}_2)}$ for the quantum group 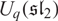$U_q(\mathfrak{sl}_2)$. In the case that 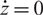$\dot z = 0$, we study the subcategory 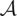$\mathcal{A}$ consisting of finite dimensional 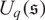$U_q(\mathfrak{s})$-modules of type 1 with zero action of Z. We directly construct an equivalence functor from 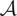$\mathcal{A}$ to the category of finite dimensional representations of an infinite quiver with some quadratic relations. As a corollary, we show that the category of finite dimensional 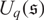$U_q(\mathfrak{s})$-modules is wild.

MSC classification

Primary: 17B10: Representations, algebraic theory (weights) 17B37: Quantum groups (quantized enveloping algebras) and related deformations 17B81: Applications to physics
Secondary: 20G42: Quantum groups (quantized function algebras) and their representations

Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 2 , May 2021 , pp. 266 - 279
Copyright
© The Author(s) 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andersen, H. H. and Mazorchuk, V., Category $\mathcal{O}$ for quantum groups, J. Eur. Math. Soc. 17 (2015), 405–431.Google Scholar
Bavula, V. V., Classication of the simple modules of the quantum Weyl algebra and the quantum plane, in Quantum Groups and Quantum Spaces (Warsaw, Banach Center Publ., 1995), vol. 40. (Warsaw: Polish Acad. Sci.), 193–201.Google Scholar
Bernshtein, I., Gelfand, I. and Gelfand, S., A certain category of $\mathfrak{g}$ -modules, Funkcional. Anal. i Prilozhen. 10(2) (1976), 1–8.Google Scholar
Bavula, V. V. and Lu, T., The prime spectrum of the algebra $K_q[X,Y]r times U_q(sl_2)$ and a classification of simple weight modules, J. Noncommut. Geom. 12(3) (2018), 889–946.CrossRefGoogle Scholar
Bavula, V. V. and Lu, T., The universal enveloping algebra $U(sl_2l \times V_2)$ , its prime spectrum and a classification of its simple weight modules. J. Lie Theory 28(2) (2018), 525–560.Google Scholar
Bavula, V. V. and Lu, T., The universal enveloping algebra of the Schrödinger algebra and its prime spectrum, Canad. Math. Bull. 61(4) (2018), 688–703.Google Scholar
Cai, Y., Cheng, Y. and Liu, G., Weight modules over the quantum Schrödinger algebra. Preprint. Revised version.Google Scholar
Cline, E., Parshall, B. and Scott, L., Finite-dimensional algebras and highest weight categories, J. Reine Angew. Math. 391 (1988), 85–99.Google Scholar
Dixmier, J., Enveloping algebras. Revised reprint of the 1977 translation. Graduate Studies in Mathematics, vol. 11 (American Mathematical Society, Providence, RI, 1996).Google Scholar
Dobrev, V. K., Doebner, H. D., Mrugalla, C., Lowest weight representations of the Schrödinger algebra and generalized heat equations, Rept. Math. Phys. 39 (1997) 201–218.Google Scholar
Dobrev, V. K., Doebner, H. D. and Mrugalla, C., A q-Schrödinger algebra, its lowest weight representations and generalized q-deformed heat/Schrödinger equations, J. Phys. A 29 (1996) 5909–5918.CrossRefGoogle Scholar
Dubsky, B., Classification of simple weight modules with finite-dimensional weight spaces over the Schrödinger algebra, Lin. Algebra Appl. 443 (2014), 204–214.CrossRefGoogle Scholar
Dubsky, B., Lu, R., Mazorchuk, V. and Zhao, K., Category $\mathcal{O}$ for the Schrödinger algebra. Linear Algebra Appl. 460 (2014), 17–50.CrossRefGoogle Scholar
Gan, W. L. and Khare, A., Quantized symplectic oscillator algebras of rank one, J. Algebra 310(2) (2007), 671–707.Google Scholar
Humphreys, J., Representations of semisimple Lie algebras in the BGG category $\mathcal{O}$ . Graduate Studies in Mathematics, vol. 94 (American Mathematical Society, Providence, RI, 2008).CrossRefGoogle Scholar
Jantzen, J. C., Lectures in quantum groups, Graduate Studies in Mathematics (American Mathematical Society, Providence, RI, 1996).CrossRefGoogle Scholar
Lü, R., Mazorchuk, V. and Zhao, K., On simple modules over conformal Galilei algebras. J. Pure Appl. Algebra 218 (2014), 1885–1899.CrossRefGoogle Scholar
Makedonskii, E., On wild and tame finite dimensional Lie Algebras. Functional Analysis and Its Applications 47(4) (2013), 271–283.CrossRefGoogle Scholar
Mazorchuk, V.. Lectures on $\mathfrak{sl}_2(\mathbb{C})$ -modules (Imperial College Press, London, 2010).Google Scholar
Tikaradze, A. and Khare, A., Center and representations of infinitesimal Hecke algebras of $sl_2$ , Comm. Algebra 38(2) (2010), 405–439.CrossRefGoogle Scholar
Perroud, M.. Projective representations of the Schrödinger group. Helv. Phys. Acta 50(2) (1977), 233–252.Google Scholar