Hostname: page-component-cb9f654ff-plnhv Total loading time: 0.001 Render date: 2025-08-08T17:05:06.548Z Has data issue: false hasContentIssue false
  • English
  • Français

JACK–LAURENT SYMMETRIC FUNCTIONS FOR SPECIAL VALUES OF PARAMETERS

Part of: Groups and algebras in quantum theory Algebraic combinatorics

Published online by Cambridge University Press:  21 July 2015

A. N. SERGEEV  and
A. P. VESELOV
A. N. SERGEEV
Affiliation:
Department of Mathematics, Saratov State University, Astrakhanskaya 83, Saratov 410012, Russia National Research University Higher School of Economics, Laboratory of Mathematical Physics, 20 Myasnitskaya Ulitsa, Moscow 101000, Russia e-mail: SergeevAN@info.sgu.ru
A. P. VESELOV
Affiliation:
Department of Mathematical Sciences, Loughborough University, Loughborough LE11 3TU, UK Moscow State University, Moscow 119899, Russia e-mail: A.P.Veselov@lboro.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the Jack–Laurent symmetric functions for special values of parameters p 0=n+k −1 m, where k is not rational and m and n are natural numbers. In general, the coefficients of such functions may have poles at these values of p 0. The action of the corresponding algebra of quantum Calogero–Moser integrals 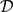$\mathcal{D}$ (k, p 0) on the space of Laurent symmetric functions defines the decomposition into generalised eigenspaces. We construct a basis in each generalised eigenspace as certain linear combinations of the Jack–Laurent symmetric functions, which are regular at p 0=n+k −1 m, and describe the action of 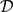$\mathcal{D}$ (k, p 0) in these eigenspaces.

MSC classification

Primary: 05E05: Symmetric functions and generalizations
Secondary: 81R12: Relations with integrable systems

Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 58 , Issue 3 , September 2016 , pp. 599 - 616
Copyright
Copyright © Glasgow Mathematical Journal Trust 2015 

References

REFERENCES

1. Bernstein, J. N. and Gelfand, S. I., Tensor products of finite and infinite dimensional representations of semisimple Lie algebras, Compos. Math. 41 (2) (1980), 245–285.Google Scholar
2. Van Diejen, J. F. and Vinet, L. (Editors), Calogero-Moser-Sutherland models (Montreal, QC, 1997), CRM Ser. Math. Phys. (Springer, New York, 2000), 23–35.Google Scholar
3. Feigin, B., Jimbo, M., Miwa, T. and Mukhin, E., A differential ideal of symmetric polynomials spanned by Jack polynomials at β = −(r−1)/(k+1), IMRN 2002 (23) (2002), 1223–1237.Google Scholar
4. Kasatani, M., Miwa, T., Sergeev, A. N. and Veselov, A. P., Coincident root loci and Jack and Macdonald polynomials for special values of the parameters, In [5], 207–225.Google Scholar
5. Kuznetsov, V. B. and Sahi, S. (Editors), Jack, Hall-Littlewood and Macdonald polynomials, Contemporary Maths, vol. 417 (American Math. Society, Providence, RI, 2006).CrossRefGoogle Scholar
6. Macdonald, I. G., Symmetric functions and Hall polynomials, 2nd edition (Oxford University Press, 1995).Google Scholar
7. Sergeev, A. N. and Veselov, A. P., Jack–Laurent symmetric functions, arXiv.org/1310.2462. Accepted for publication in Proc. London Math. Soc., 2015.Google Scholar
8. Zuckerman, G., Tensor products of finite and infinite dimensional representations of semisimple Lie groups, Ann. Math. 106 (2) (1977), 295–308.Google Scholar