Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kishi, Yasuhiro
and
Komatsu, Toru
2017.
Imaginary quadratic fields whose ideal class groups have 3-rank at least three.
Journal of Number Theory,
Vol. 170,
Issue. ,
p.
46.
Chakraborty, Kalyan
Hoque, Azizul
and
Sharma, Richa
2018.
Advances in Mathematical Inequalities and Applications.
p.
247.
Buell, Duncan A.
2022.
A parameterized family of quadratic class groups with 3-Sylow subgroups of rank at least three.
The Ramanujan Journal,
Vol. 59,
Issue. 3,
p.
955.
Lee, Siyun
Lee, Yoonjin
and
Yoo, Jinjoo
2023.
Infinite families of class groups of quadratic fields with 3-rank at least one: quantitative bounds.
International Journal of Number Theory,
Vol. 19,
Issue. 03,
p.
621.

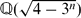 be the imaginary quadratic field and
be the imaginary quadratic field and 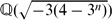 the real quadratic field. In this paper, we prove that the class number of
the real quadratic field. In this paper, we prove that the class number of 