Contents
Research Article
WEAKLY PERFECT GRAPHS ARISING FROM RINGS
-
- Published online by Cambridge University Press:
- 22 March 2010, pp. 417-425
-
- Article
-
- You have access
- Export citation
DECOMPOSITIONS OF COUNTABLE LINEAR TRANSFORMATIONS
-
- Published online by Cambridge University Press:
- 22 March 2010, pp. 427-433
-
- Article
-
- You have access
- Export citation
STRONGLY BOUNDED REPRESENTING MEASURES AND CONVERGENCE THEOREMS
-
- Published online by Cambridge University Press:
- 22 March 2010, pp. 435-445
-
- Article
-
- You have access
- Export citation
A GALOIS THEORY FOR THE FIELD EXTENSION K((X))/K
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 447-451
-
- Article
-
- You have access
- Export citation
A GENERALISED KUMMER'S CONJECTURE
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 453-472
-
- Article
-
- You have access
- Export citation
THE NON-ABELIAN TENSOR PRODUCT OF FINITE GROUPS IS FINITE: A HOMOLOGY-FREE PROOF
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 473-477
-
- Article
-
- You have access
- Export citation
BIFLATNESS AND BIPROJECTIVITY OF BANACH ALGEBRAS GRADED OVER A SEMILATTICE
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 479-495
-
- Article
-
- You have access
- Export citation
THIRD-REGULAR BI-EMBEDDINGS OF LATIN SQUARES
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 497-503
-
- Article
-
- You have access
- Export citation
POSITIVE SOLUTIONS TO p(x)-LAPLACIAN–DIRICHLET PROBLEMS WITH SIGN-CHANGING NON-LINEARITIES
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 505-516
-
- Article
-
- You have access
- Export citation
ON AN EIGENVALUE PROBLEM FOR AN ANISOTROPIC ELLIPTIC EQUATION INVOLVING VARIABLE EXPONENTS
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 517-527
-
- Article
-
- You have access
- Export citation
DECOMPOSITION OF JORDAN AUTOMORPHISMS OF TRIANGULAR MATRIX ALGEBRA OVER COMMUTATIVE RINGS
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 529-536
-
- Article
-
- You have access
- Export citation
PULLBACK ATTRACTORS FOR A NON-AUTONOMOUS SEMI-LINEAR DEGENERATE PARABOLIC EQUATION
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 537-554
-
- Article
-
- You have access
- Export citation
CLASSIFYING CLOSED 2-ORBIFOLDS WITH EULER CHARACTERISTICS
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 555-574
-
- Article
-
- You have access
- Export citation
ON THE IDEAL CLASS GROUP OF CERTAIN QUADRATIC FIELDS
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 575-581
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC EQUIVALENCE OF ALMOST PERIODIC SOLUTIONS FOR A CLASS OF PERTURBED ALMOST PERIODIC SYSTEMS
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 583-592
-
- Article
-
- You have access
- Export citation
ON STABILIZERS OF SOME TEICHMÜLLER DISKS IN POINTED MAPPING CLASS GROUPS
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 593-604
-
- Article
-
- You have access
- Export citation
ON GENERALIZATION OF NAKAYAMA'S LEMMA
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 605-617
-
- Article
-
- You have access
- Export citation
THE BOUNDARY CONDITIONS DESCRIPTION OF TYPE I DOMAINS
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 619-633
-
- Article
-
- You have access
- Export citation
LINEAR WEINGARTEN HYPERSURFACES IN A REAL SPACE FORM
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 635-648
-
- Article
-
- You have access
- Export citation
DERIVED H-MODULE ENDOMORPHISM RINGS
-
- Published online by Cambridge University Press:
- 25 August 2010, pp. 649-661
-
- Article
-
- You have access
- Export citation

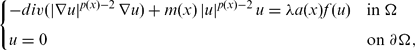
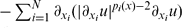 = λ|
= λ|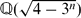 be the imaginary quadratic field and
be the imaginary quadratic field and 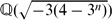 the real quadratic field. In this paper, we prove that the class number of
the real quadratic field. In this paper, we prove that the class number of 
 ), 1 ≤
), 1 ≤