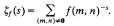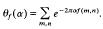Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 274
A generalized Drazin inverse
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 367-381
-
- Article
-
- You have access
- Export citation
- Cited by 243
On the distance of the composition of two derivations to the generalized derivations
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 89-93
-
- Article
-
- You have access
- Export citation
- Cited by 177
SLANT SUBMANIFOLDS IN SASAKIANMANIFOLDS
-
- Published online by Cambridge University Press:
- 07 August 2001, pp. 125-138
-
- Article
-
- You have access
- Export citation
- Cited by 164
The discrete and continuous Painlevé VI hierarchy and the Garnier systems
-
- Published online by Cambridge University Press:
- 19 July 2002, pp. 109-123
-
- Article
-
- You have access
- Export citation
- Cited by 151
The Closest Packing of Spherical Caps in n Dimensions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 139-144
-
- Article
-
- You have access
- Export citation
- Cited by 140
Some properties of non-commutative regular graded rings
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 277-300
-
- Article
-
- You have access
- Export citation
- Cited by 130
Relations between Ricci curvature and shape operator for submanifolds with arbitrary codimensions
-
- Published online by Cambridge University Press:
- 19 July 2001, pp. 33-41
-
- Article
-
- You have access
- Export citation
- Cited by 116
On products of idempotent matrices
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 118-122
-
- Article
-
- You have access
- Export citation
- Cited by 115
On Certain Dual Integral Equations
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 21-24
-
- Article
-
- You have access
- Export citation
- Cited by 113
Axiomatisations of the average and a further generalisation of monotonic sequences
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 63-65
-
- Article
-
- You have access
- Export citation
- Cited by 105
On quasi-duo rings
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 21-31
-
- Article
-
- You have access
- Export citation
- Cited by 92
Proof of a conjecture of Ramanujan
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 14-32
-
- Article
-
- You have access
- Export citation
- Cited by 87
Bisimple ω-Semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 160-167
-
- Article
-
- You have access
- Export citation
- Cited by 87
RINGS IN WHICH ELEMENTS ARE UNIQUELY THE SUM OF AN IDEMPOTENT AND A UNIT
-
- Published online by Cambridge University Press:
- 19 May 2004, pp. 227-236
-
- Article
-
- You have access
- Export citation
- Cited by 87
Mean curvature and shape operator of isometric immersions in real-space-forms
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 87-97
-
- Article
-
- You have access
- Export citation
- Cited by 86
Generalisation de la decomposition de kato aux opérateurs paranormaux et spectraux
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 159-175
-
- Article
-
- You have access
- Export citation
- Cited by 84
On semi B-Fredholm operators
-
- Published online by Cambridge University Press:
- 25 July 2002, pp. 457-465
-
- Article
-
- You have access
- Export citation
- Cited by 82
Remarks on Weak Compactness in L1(μ,X)
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 87-91
-
- Article
-
- You have access
- Export citation
- Cited by 80
Minimal theta functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 75-85
-
- Article
-
- You have access
- Export citation
- Cited by 79
DUO MODULES
-
- Published online by Cambridge University Press:
- 06 December 2006, pp. 533-545
-
- Article
-
- You have access
- Export citation

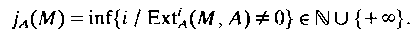
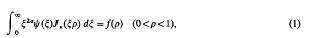

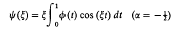
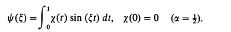
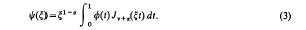
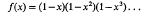
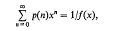
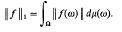
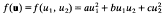 be a positive definite binary quadratic form with real coefficients and discriminant
be a positive definite binary quadratic form with real coefficients and discriminant 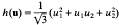 . The Epstein zeta function of
. The Epstein zeta function of