Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Weiqiong
and
Han, Di
2013.
An identity involving certain Hardy sums and Ramanujan’s sum.
Advances in Difference Equations,
Vol. 2013,
Issue. 1,
Han, Di
and
Zhang, Wenpeng
2013.
Upper bound estimate of character sums over Lehmer’s numbers.
Journal of Inequalities and Applications,
Vol. 2013,
Issue. 1,
Chao, Xiaoli
and
Wang, Peijun
2014.
LINEAR WEINGARTEN HYPERSURFACES IN RIEMANNIAN SPACE FORMS.
Bulletin of the Korean Mathematical Society,
Vol. 51,
Issue. 2,
p.
567.
Xu, Hong-wei
and
Xu, Zhi-yuan
2014.
A new characterization of the Clifford torus via scalar curvature pinching.
Journal of Functional Analysis,
Vol. 267,
Issue. 10,
p.
3931.
Zhang, Han
and
Zhang, Wenpeng
2015.
Some new sums related to D. H. Lehmer problem.
Czechoslovak Mathematical Journal,
Vol. 65,
Issue. 4,
p.
915.

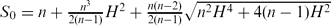 .
.