Contents
Research Article
A class of groups rich in finite quotients
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 263-274
-
- Article
-
- You have access
- Export citation
Finite groups of outer automorphisms of free groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 275-282
-
- Article
-
- You have access
- Export citation
Prime ideals of quantized Weyl algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 283-297
-
- Article
-
- You have access
- Export citation
A problem of Hooley in Diophantine approximation
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 299-308
-
- Article
-
- You have access
- Export citation
Spectra of conjugated ideals in group algebras of abelian groups of finite rank and control theorems
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 309-320
-
- Article
-
- You have access
- Export citation
Primary decompositions over domains
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 321-326
-
- Article
-
- You have access
- Export citation
Khinchin's inequality for operators
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 327-336
-
- Article
-
- You have access
- Export citation
Some remarks on the p-homotopy type of B∑p2
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 337-342
-
- Article
-
- You have access
- Export citation
Complete submanifolds with parallel mean curvature in a sphere
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 343-346
-
- Article
-
- You have access
- Export citation
The kernel relation for a strict extension of certain regular semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 347-357
-
- Article
-
- You have access
- Export citation
Co-Cohen-Macaulay Artinian modules over commutative rings
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 359-366
-
- Article
-
- You have access
- Export citation
A generalized Drazin inverse
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 367-381
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 38 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f8
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 38 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
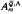 which arises from the work of Maltsiniotis [10] on noncommutative differential calculus. This algebra has been studied from the point of view of noncommutative ring theory by various authors including Alev and Dumas [1], the second author [9], Cauchon [3], and Goodearl and Lenagan [5]. In [9], it is shown that
which arises from the work of Maltsiniotis [10] on noncommutative differential calculus. This algebra has been studied from the point of view of noncommutative ring theory by various authors including Alev and Dumas [1], the second author [9], Cauchon [3], and Goodearl and Lenagan [5]. In [9], it is shown that 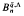 obtained on inverting these elements is simple of Krull and global dimension
obtained on inverting these elements is simple of Krull and global dimension 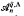 . This algebra has more symmetric defining relations than those of
. This algebra has more symmetric defining relations than those of 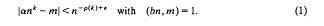
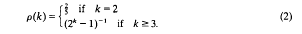
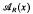 the annihilator of
the annihilator of 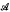 be either a
be either a 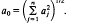 .
.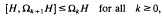
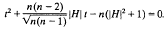
 (
( , the kernel of
, the kernel of 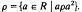 . The relation
. The relation