Introduction
The field of exoplanetary science has witnessed many rapid and exciting advances over the past couple of decades. With the number of discovered exoplanets now numbering in the thousands (Winn & Fabrycky Reference Winn and Fabrycky2015), there has been a great deal of interest in identifying planets that are habitable, i.e. potentially capable of bearing life (Kasting & Catling Reference Kasting and Catling2003; Chyba & Hand Reference Chyba and Hand2005; Lammer et al. Reference Lammer2009; Cockell et al. Reference Cockell2016). To this end, most of the current discoveries have been centered around planets orbiting M-dwarfs since they are more abundant, and easier to detect (Scalo et al. Reference Scalo2007; Tarter et al. Reference Tarter2007; Shields et al. Reference Shields, Ballard and Johnson2016). It is now believed that there are ~ 1010 habitable planets in our own Galaxy (Kasting et al. Reference Kasting, Kopparapu, Ramirez and Harman2014; Dressing & Charbonneau Reference Dressing and Charbonneau2015).
In recent times, several major discoveries have provided additional impetus to studies of habitability. The first was the discovery of an Earth-mass exoplanet in the habitable zone (HZ) – the region capable of sustaining liquid water on the planet's surface – around Proxima Centauri, the nearest star to our Solar System at only 4.2 light years away (Anglada-Escudé et al. Reference Anglada-Escudé2016). There are plans already underway to explore this planet, dubbed Proxima b, via a flyby mission.Footnote 1 The second major advance was the discovery of at least seven Earth-sized planets transiting the ultracool dwarf star TRAPPIST-1 at a distance of 39.5 light years (Gillon et al. Reference Gillon2016, Reference Gillon2017). The presence of three planets in the HZ around TRAPPIST-1 therefore presents a unique opportunity for studying multiple planets that may host life (Lingam & Loeb Reference Lingam and Loeb2017). The discovery of the temperate super-Earth LHS 1140b transiting an M-dwarf at a distance of 39 light years also merits a mention (Dittmann et al. Reference Dittmann2017).
It is worth emphasizing that the existence of a planet in the HZ does not imply life exists on the planet, or even that it will necessarily be able to support a biosphere. Most of the current assessments of habitable planets have tended to focus on superficial metrics, which can be misleading, as rightly pointed out in Schulze-Makuch & Guinan (Reference Schulze-Makuch and Guinan2016) and Tasker et al. (Reference Tasker2017). These metrics evaluate the degree of similarity between certain, physically relevant, parameters of a given exoplanet and the Earth, and have led to unfortunate misconceptions that planets with higher values (of the similarity indices) are automatically more habitable.
In this paper, we attempt to advance the assessment of life-bearing planets by identifying physical processes that play a major role in governing habitability through the formulation of likelihood functions that depend on basic planetary and stellar parameters. By doing so, we expect to pave the way towards understanding the complex relationship between the aforementioned parameters and the likelihood of a planet hosting life in reality (Lineweaver & Chopra Reference Lineweaver and Chopra2012; Cockell et al. Reference Cockell2016).
The role of planetary temperature
We begin by outlining the centrality of temperature in regulating a diverse array of ecological and evolutionary parameters and processes (Cossins & Bowler Reference Cossins and Bowler1987; Brown et al. Reference Brown, Gillooly, Allen, Savage and West2004; Deutsch et al. Reference Deutsch, Tewksbury, Huey, Sheldon, Ghalambor, Haak and Martin2008; Kingsolver & Huey Reference Kingsolver and Huey2008; Angilletta Reference Angilletta2009; Dillon et al. Reference Dillon, Wang and Huey2010) by adopting the general premise that biochemical reactions analogous to metabolism are universal on life-bearing exoplanets (Pace Reference Pace2001; Benner et al. Reference Benner, Ricardo and Carrigan2004; Ball Reference Ball2008). Subsequently, we construct a global likelihood function for these processes that depends on the planetary temperature.
The metabolic theory of ecology and temperature
We adopt the tenets of the metabolic theory of ecology (MTE) that relies on the assumption that the metabolic rate B of organisms plays a major role in governing macroecological processes. The reader may consult West et al. (Reference West, Brown and Enquist2001); Agutter & Wheatley (Reference Agutter and Wheatley2004); Brown et al. (Reference Brown, Gillooly, Allen, Savage and West2004); Clarke & Fraser (Reference Clarke and Fraser2004); Marquet et al. (Reference Marquet, Quiñones, Abades, Labra, Tognelli, Arim and Rivadeneira2005); Clarke (Reference Clarke2006); Savage et al. (Reference Savage, Deeds and Fontana2008); Price et al. (Reference Price2012); Humphries & McCann (Reference Humphries and McCann2014); Glazier (Reference Glazier2015) for comprehensive reviews, assessments and critiques of this field. We have chosen to work with this model since it attempts to quantify important ecological patterns and parameters by adopting a mechanistic perspective based on generic physical and chemical considerations, without the necessity for invoking complex (and specific) biological factors. Naturally, this approach has attracted a fair amount of criticism as outlined in the aforementioned references. Nevertheless, we will operate under the premise that the basic underpinnings of the MTE are valid for ecosystems on other planets, at least for those capable of sustaining life-as-we-know-it.
The MTE is founded on the principle that the metabolic rate, which serves as its cornerstone, scales as,
where m is the mass of the organism, k
B is the Boltzmann constant, T is the absolute temperature, and E is the average activation energy, which is determined by considering the appropriate rate-limiting step in metabolism (Gillooly et al.
Reference Gillooly, Brown, West, Savage and Charnov2001). Now, suppose that one wished to formulate a ‘mean’ metabolic rate
![]() $\bar B$
across all species. This can be done by introducing the distribution function for the number of individuals with a given mass N(m) as follows,
$\bar B$
across all species. This can be done by introducing the distribution function for the number of individuals with a given mass N(m) as follows,
The last scaling follows if E(m, T) ≈ E(T), i.e. provided that the activation energy displays a weak dependence on the organism's mass.Footnote 2 This appears to be a fairly robust assumption on Earth, since E falls within a fairly narrow band of energies ranging between 0.6 and 0.7 eV, for unicellular organisms, plants, ectotherms and endotherms (Gillooly et al. Reference Gillooly, Brown, West, Savage and Charnov2001; Brown et al. Reference Brown, Gillooly, Allen, Savage and West2004). It was pointed out in Gillooly et al. (Reference Gillooly, Allen, Savage, Charnov, West and Brown2006) that the mean value of E = 0.65 eV is nearly equal to the average activation energy of 0.66 eV that arises from the rate of ATP synthesis in isolated mitochondria.
One of the central predictions of the MTE is that several ecological parameters are regulated by the metabolic rate, and are thus expected to depend on the temperature via the Boltzmann factor inherent in equation (1). Examples of these parameters, which have been studied empirically, include:
-
• The production and turnover of biomass, and the rate of biological energy flux per unit area (Enquist et al. Reference Enquist, Economo, Huxman, Allen, Ignace and Gillooly2003; Brown et al. Reference Brown, Gillooly, Allen, Savage and West2004).
-
• The maximal rates of population growth and molecular evolution (Brown et al. Reference Brown, Gillooly, Allen, Savage and West2004; Savage et al. Reference Savage, Gillooly, Brown, West and Charnov2004; Gillooly et al. Reference Gillooly, Allen, West and Brown2005), and the reciprocal developmental time (Gillooly et al. Reference Gillooly, Charnov, West, Savage and Brown2002).
-
• The rates of genetic divergence and speciation, species diversity and coexistence, and trophic interactions (Allen et al. Reference Allen, Brown and Gillooly2002, Reference Allen, Gillooly, Savage and Brown2006; Dell et al. Reference Dell, Pawar and Savage2014).
-
• Higher biodiversity is predicted to be prevalent in habitats with hotter average temperatures (Marquet et al. Reference Marquet, Quiñones, Abades, Labra, Tognelli, Arim and Rivadeneira2005; Allen et al. Reference Allen, Gillooly, Savage and Brown2006; Fuhrman et al. Reference Fuhrman, Steele, Hewson, Schwalbach, Brown, Green and Brown2008; Wang et al. Reference Wang, Brown, Tang and Fang2009). This pattern has been proven to be valid on Earth, which is characterized by distinctive latitudinal gradients in species richness (Gaston Reference Gaston2000), although other factors, such as the degree of precipitation, also play an important (but possibly sub-dominant) role (Moles et al. Reference Moles2014).
The Boltzmann factor dependence implies that all of the above quantities are expected to monotonically increase with temperature. This is closely related to the notion that ‘Hotter is better’, which posits that a higher value of T is correlated with enhanced growth, fitness and diversity (Thompson Reference Thompson1942; Kingsolver & Huey Reference Kingsolver and Huey2008; Mayhew et al. Reference Mayhew, Bell, Benton and McGowan2012), up to a particular limit.
At this stage, some important caveats are in order. The first stems from critiques concerning the validity and interpretation of the MTE (Clarke & Fraser Reference Clarke and Fraser2004; Clarke Reference Clarke2006; Downs et al. Reference Downs, Hayes and Tracy2008; Price et al. Reference Price2012; Glazier Reference Glazier2015). In addition, the monotonically increasing trend with temperature cannot continue ad infinitum since thermal adaptation breaks down beyond a certain point (Angilletta Reference Angilletta2009; Corkrey et al. Reference Corkrey, Olley, Ratkowsky, McMeekin and Ross2012; Schulte Reference Schulte2015). Moreover, there exist several important and subtle ambiguities in resolving the exact relationship between temperature and the aforementioned traits (Clarke Reference Clarke2006; Clarke & Rothery Reference Clarke and Rothery2008; Kingsolver Reference Kingsolver2009). Lastly, our analysis has presupposed a steady-state temperature, but rapid fluctuations can engender mass extinctions and irreversible changes in the biosphere (Purvis & Hector Reference Purvis and Hector2000; Barnosky et al. Reference Barnosky2012; Frank & Sullivan Reference Frank and Sullivan2014).
The temperature-dependent likelihood function
Based on the preceding discussion, we introduce the likelihood factor for biodiversity which has been adapted from equation (2),
where E and T are now taken to be the mean activation energy and temperature respectively. The θ is the Heavyside function, which ensures that the likelihood becomes zero for T <T L and T >T U.
The limits of Earth-based lifeforms range from 262 to 395 K (Rothschild & Mancinelli Reference Rothschild and Mancinelli2001; McKay Reference McKay2014), while the corresponding range for photosynthetic lifeforms is narrower since the upper bound is lowered to 348 K (Kiang et al. Reference Kiang, Siefert, Govindjee and Blankenship2007). Note that T corresponds to the average surface temperature of the planet in our subsequent analysis, because we are interested in quantifying the likelihood on a planetary scale. Thus, instead of T representing the temperature of the local habitat (for ectotherms) or the average internal temperature (for endotherms), we have replaced it by the overall planetary surface temperature. Naturally, a limitation of this methodology is that it represents a coarse-grained estimate that smears out local effects.Footnote 3
We are now in a position to construct the ‘normalized’ (Earth-referenced) temperature-based likelihood with respect to the Earth,
where T U and T L should be interpreted as the limits over which the Boltzmann factor is valid. Clearly, the simple ansatz exemplified by equation (3) corresponds to sharp (discontinuous) cutoffs, and we refer the reader to Corkrey et al. (Reference Corkrey, Olley, Ratkowsky, McMeekin and Ross2012); Dell et al. (Reference Dell, Pawar and Savage2014); Schulte (Reference Schulte2015); Corkrey et al. (Reference Corkrey, McMeekin, Bowman, Ratkowsky, Olley and Ross2016), wherein more sophisticated and realistic variants have been delineated. The temperature range T L<T <T U is not expected to exceed the Earth-based photosynthesis limits for life-as-we-know-it.Footnote 4 We have also introduced the auxiliary parameter δ in equation (4),
where
![]() $E_ \oplus = 0.66\,{\rm eV}$
(Dell et al.
Reference Dell, Pawar and Savage2011) and
$E_ \oplus = 0.66\,{\rm eV}$
(Dell et al.
Reference Dell, Pawar and Savage2011) and
![]() $T_ \oplus = 287\,K$
are the corresponding values for the Earth. The last relation follows from
$T_ \oplus = 287\,K$
are the corresponding values for the Earth. The last relation follows from
![]() $E{\rm \sim} E_ \oplus $
since we only consider life-as-we-know-it in our present analysis. If we substitute T = 218 K for Mars, we find that
$E{\rm \sim} E_ \oplus $
since we only consider life-as-we-know-it in our present analysis. If we substitute T = 218 K for Mars, we find that
![]() ${ {\cal P}}_{\rm T} = 0$
because of the Heavyside function. In contrast, the equatorial temperatures on Mars can exceed T
L, thereby giving rise to a finite value of
${ {\cal P}}_{\rm T} = 0$
because of the Heavyside function. In contrast, the equatorial temperatures on Mars can exceed T
L, thereby giving rise to a finite value of
![]() ${ {\cal P}}_{\rm T} $
locally. If we consider Venus instead, it is evident that
${ {\cal P}}_{\rm T} $
locally. If we consider Venus instead, it is evident that
![]() ${ {\cal P}}_{\rm T} = 0$
since T ≫ T
U.
${ {\cal P}}_{\rm T} = 0$
since T ≫ T
U.
Thus, to conclude, we have hypothesized that equation (4) quantifies the likelihood of complex life-sustaining processes as a function of the planet's surface temperature.Footnote 5 This function serves as a proxy for the (relative) metabolic rate, which, in turn, has been hypothesized to regulate important biological parameters, such as the species diversity, biological fluxes, and the rates of speciation and growth to name a few. Hence, if abiogenesis had been successfully initiated on a particular planet, the chances of complex life emerging are expected to be correspondingly greater for higher temperatures since: (i) the rates of evolution and speciation are enhanced, and (ii) a greater diversity of species are potentially sustainable. Hence, this metric arguably constitutes a more sophisticated variant of understanding the likelihood of macroecological processes on exoplanets. However, we must reiterate that this likelihood function is not synonymous with a planet being habitable since there are myriad factors involved in the latter. Furthermore, equation (4) does not quantify the likelihood of abiogenesis, and the existence of the aforementioned ecological and evolutionary processes is obviously contingent upon life successfully originating (and diversifying) on the planet.
Although we have not directly estimated the prospects for abiogenesis on exoplanets, we wish to point out that several studies have presented empirical and theoretical evidence favouring a high-temperature origin of life (OOL; Pace Reference Pace1991; Gaucher et al. Reference Gaucher, Thomson, Burgan and Benner2003; Martin et al. Reference Martin, Baross, Kelley and Russell2008; Akanuma et al. Reference Akanuma, Nakajima, Yokobori, Kimura, Nemoto, Mase, Miyazono, Tanokura and Yamagishi2013), although many factors still remain poorly known (Miller & Lazcano Reference Miller and Lazcano1995). If life did indeed originate in a high-temperature environment, perhaps the likelihood of abiogenesis could exhibit a Boltzmann factor dependence on the temperature akin to equation (2), thereby favouring thermophilic ancestral lifeforms (Weiss et al. Reference Weiss, Sousa, Mrnjavac, Neukirchen, Roettger, Nelson-Sathi and Martin2016). However, an important point worth highlighting is that the temperature alluded to when discussing abiogenesis always represents the in situ value (e.g. at hydrothermal vents), and not the global planetary temperature.
The role of atmospheric escape
Next, we explore the constraints on the likelihood (of a planet being habitable) that are set by atmospheric escape. Before doing so, a few general observations are in order.
The phase diagram of water requires external pressure in order for liquid water to emerge upon warming solid ice (McKay Reference McKay2014). It is therefore widely presumed that complex, surface-based, organic chemistry corresponding to life-as-we-know-it necessitates the existence of an atmosphere (Lammer et al. Reference Lammer2009; Cockell et al. Reference Cockell2016). However, atmospheres can be eroded through a diverse array of processes, such as thermal escape, photochemical escape and multiple non-thermal mechanisms such as sputtering (Johnson et al. Reference Johnson, Combi, Fox, Ip, Leblanc, McGrath, Shematovich, Strobel and Waite2008; Seager Reference Seager2010; Lammer Reference Lammer2013).Footnote 6 On the other hand, they can also be replenished through volcanism, giant impacts and evaporation of oceans (Kasting & Catling Reference Kasting and Catling2003). If the associated timescales for the escape processes are ‘fast’, there may not exist sufficient time for complex life to emerge and evolve. Thus, we shall suppose henceforth that the timescales for atmospheric escape, which can be quantified in some instances, will serve as effective constraints for determining the inclination towards habitability of a given exoplanet relative to Earth.
In actuality, there are several important and distinct timescales that must be taken into account in conjunction with the planet's age (t P). Some of the notable ones are as follows:
-
• The characteristic timescale(s) involved in the depletion of the planetary atmosphere (t ℓ), which will be the focus of this paper.
-
• The minimum timescale required for abiogenesis – the OOL – to commence (t OOL), since the likelihood of life arising on the planet is zero for t P < t OOL. As per current evidence, it seems plausible that
 $t_{{\rm OOL}} {\lesssim} 500$
Myr on Earth (Bell et al.
Reference Bell, Boehnke, Harrison and Mao2015; Dodd et al.
Reference Dodd, Papineau, Grenne, Slack, Rittner, Pirajno, O'Neil and Little2017) although, in light of the many uncertainties involved, this timescale ought not be perceived as being definitive.
$t_{{\rm OOL}} {\lesssim} 500$
Myr on Earth (Bell et al.
Reference Bell, Boehnke, Harrison and Mao2015; Dodd et al.
Reference Dodd, Papineau, Grenne, Slack, Rittner, Pirajno, O'Neil and Little2017) although, in light of the many uncertainties involved, this timescale ought not be perceived as being definitive. -
• The timescale over which the planet will be subjected to the extended pre-main-sequence (pre-MS) phase (t PMS), since this can adversely impact habitability (extreme water loss), especially when dealing with exoplanets in the HZ of M-dwarfs (Ramirez & Kaltenegger Reference Ramirez and Kaltenegger2014; Luger & Barnes Reference Luger and Barnes2015; Tian & Ida Reference Tian and Ida2015).
-
• The duration of time taken for a given planet to ‘enter’ the outer edge of the HZ (t OHZ), and to finally ‘exit’ the inner edge of the HZ (t IHZ), since the HZ itself evolves over time (Rushby et al. Reference Rushby, Claire, Osborn and Watson2013). By construction, t P < t OHZ or t P > t IHZ imply the planet would not be habitable (in the conventional sense).
Thus, we shall implicitly restrict our attention to planets where t P > t OOL, tOHZ < t P < t IHZ, and the pre-MS phase has not rendered the planet uninhabitable.
Timescales for atmospheric escape
As noted earlier, there are several mechanisms that lead to atmospheric losses. In our analysis, we shall consider two dominant causes, namely, hydrodynamic escape and stellar wind stripping. We do not evaluate the extent of Jeans escape, as it does not play a major role in facilitating escape of heavier molecules (such as O2 and CO2) from Earth-like planets in the HZ (Lammer Reference Lammer2013).
For hydrodynamic escape, we rely upon the assumption of energy-limited escape (Seager Reference Seager2010), enabling us to estimate the lifetime of the planet's atmosphere as,
where M atm, M p and R p are the mass of the atmosphere, mass and radius of the planet, respectively; 〈F EUV〉 is the average extreme ultraviolet (EUV) flux while β and η are phenomenological parameters. Further details concerning the derivation of equation (6) can be found in Chapter 4 of Seager (Reference Seager2010) and Section 2 of Owen & Alvarez (Reference Owen and Alvarez2016). Other forms of UV-driven atmospheric loss include recombination-limited and photon-limited escape (Owen & Alvarez Reference Owen and Alvarez2016).
Next, we consider stripping of the atmosphere by the stellar wind. The associated timescales are given by t MSW and t UMSW for the magnetized and unmagnetized cases (with and without an intrinsic dipole field). Note that we are interested in the fastest timescale for atmospheric loss, thereby leading us to t ℓ = min{t HD, t UMSW} or t ℓ = min{t HD, t MSW} depending on the situation. However, the escape rates for magnetized planets are usually expected to be somewhat lower (Lammer Reference Lammer2013; Ehlmann et al. Reference Ehlmann2016; Dong et al. Reference Dong, Lingam, Ma and Cohen2017b), implying that t UMSW <t MSW.
In fact, for most exoplanets in the HZ around M-dwarfs, the dynamic pressure exerted by the stellar wind is so great that the additional shielding offered by the planet's magnetic field B P is relatively unimportant (Garraffo et al. Reference Garraffo, Drake and Cohen2016; Airapetian et al. Reference Airapetian, Glocer, Khazanov, Loyd, France, Sojka, Danchi and Liemohn2017; Dong et al. Reference Dong, Lingam, Ma and Cohen2017b), provided that B P is not anomalously high (Vidotto et al. Reference Vidotto, Jardine, Morin, Donati, Lang and Russell2013). By utilizing standard dynamo scaling laws (Christensen Reference Christensen2010), it can be shown that B P will not be very large if the convected heat flux in the planetary core is not significantly higher than that of the Earth. In fact, tidally locked exoplanets, expected to be fairly common in the HZ around M-dwarfs, are typically associated with weak magnetic moments (Khodachenko et al. Reference Khodachenko2007; Shields et al. Reference Shields, Ballard and Johnson2016).
Based on the above set of arguments, we may henceforth adopt t UMSW ~ t MSW for certain M-dwarf exoplanets. The timescale of atmospheric loss for unmagnetized planets (t SW) is given by,
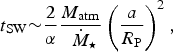 $$t_{{\rm SW}} {\rm \sim} \displaystyle{2 \over \alpha} \displaystyle{{M_{{\rm atm}}} \over \dot {{\hskip4pt}M_{\rm \star}}} \left( {\displaystyle{a \over {R_{\rm P}}}} \right)^2, $$
$$t_{{\rm SW}} {\rm \sim} \displaystyle{2 \over \alpha} \displaystyle{{M_{{\rm atm}}} \over \dot {{\hskip4pt}M_{\rm \star}}} \left( {\displaystyle{a \over {R_{\rm P}}}} \right)^2, $$
where a is the semi-major axis of the planet,
![]() ${\hskip-4pt}\dot {{\hskip4pt}M_{\rm \star}} $
is the stellar mass loss rate and α is the entrainment efficiency that is treated as a constant (Zendejas et al.
Reference Zendejas, Segura and Raga2010). The above formula was verified to be fairly accurate by means of numerical simulations in Dong et al. (Reference Dong, Jin, Lingam, Airapetian, Ma and van der Holst2017a).
${\hskip-4pt}\dot {{\hskip4pt}M_{\rm \star}} $
is the stellar mass loss rate and α is the entrainment efficiency that is treated as a constant (Zendejas et al.
Reference Zendejas, Segura and Raga2010). The above formula was verified to be fairly accurate by means of numerical simulations in Dong et al. (Reference Dong, Jin, Lingam, Airapetian, Ma and van der Holst2017a).
Contribution of atmospheric loss to the likelihood function
Following our preceding discussion, the atmospheric loss is given by t ℓ = min{t HD, t SW}, where t HD and t SW are given by equations (6) and (7), respectively. We define the normalized (Earth-referenced) likelihood of this timescale in the following manner:
where
![]() $t_ \oplus $
is the corresponding value of t
ℓ upon substituting Earth's parameters. When t
HD <t
SW, we find that equation (8) simplifies to,
$t_ \oplus $
is the corresponding value of t
ℓ upon substituting Earth's parameters. When t
HD <t
SW, we find that equation (8) simplifies to,
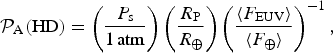 $${ {\cal P}}_{\rm A} ({\rm HD}) = \left( {\displaystyle{{P_{\rm s}} \over {1{\kern 1pt} {\rm atm}}}} \right)\left( {\displaystyle{{R_{\rm P}} \over {R_ \oplus}}} \right)\left( {\displaystyle{{\langle F_{{\rm EUV}} \rangle} \over {\langle F_ \oplus \rangle}}} \right)^{ - 1}, $$
$${ {\cal P}}_{\rm A} ({\rm HD}) = \left( {\displaystyle{{P_{\rm s}} \over {1{\kern 1pt} {\rm atm}}}} \right)\left( {\displaystyle{{R_{\rm P}} \over {R_ \oplus}}} \right)\left( {\displaystyle{{\langle F_{{\rm EUV}} \rangle} \over {\langle F_ \oplus \rangle}}} \right)^{ - 1}, $$
where
![]() $P_{\rm s} = gM_{{\rm atm}} /(4\pi R_{\rm P}^2 )$
is the surface pressure of the atmosphere,
$P_{\rm s} = gM_{{\rm atm}} /(4\pi R_{\rm P}^2 )$
is the surface pressure of the atmosphere,
![]() $F_ \oplus $
is the value of 〈F
EUV〉 for the Earth and we have employed the mass–radius relation
$F_ \oplus $
is the value of 〈F
EUV〉 for the Earth and we have employed the mass–radius relation
![]() $M/M_ \oplus {\rm \sim} \left( {R/R_ \oplus } \right)^{3.7} $
(Valencia et al.
Reference Valencia, O'Connell and Sasselov2006; Zeng et al.
Reference Zeng, Sasselov and Jacobsen2016). Similarly, when t
HD >t
SW, it is easy to verify that equation (8) can be expressed as,
$M/M_ \oplus {\rm \sim} \left( {R/R_ \oplus } \right)^{3.7} $
(Valencia et al.
Reference Valencia, O'Connell and Sasselov2006; Zeng et al.
Reference Zeng, Sasselov and Jacobsen2016). Similarly, when t
HD >t
SW, it is easy to verify that equation (8) can be expressed as,
 $${ {\cal P}}_{\rm A} ({\rm SW}) = \left( {\displaystyle{{P_{\rm s}} \over {1{\kern 1pt} {\rm atm}}}} \right)\left( {\displaystyle{a \over {1{\kern 1pt} {\rm AU}}}} \right)^2 \left( {\displaystyle{{R_{\rm P}} \over {R_ \oplus}}} \right)^{ - 1.7} \left( {\displaystyle{\dot {{\hskip4pt}M_{\rm \star}} \over \dot {{\hskip4pt}M_{\rm \odot}}}} \right)^{ - 1}, $$
$${ {\cal P}}_{\rm A} ({\rm SW}) = \left( {\displaystyle{{P_{\rm s}} \over {1{\kern 1pt} {\rm atm}}}} \right)\left( {\displaystyle{a \over {1{\kern 1pt} {\rm AU}}}} \right)^2 \left( {\displaystyle{{R_{\rm P}} \over {R_ \oplus}}} \right)^{ - 1.7} \left( {\displaystyle{\dot {{\hskip4pt}M_{\rm \star}} \over \dot {{\hskip4pt}M_{\rm \odot}}}} \right)^{ - 1}, $$
where
![]() ${\dot {{\hskip4pt}M_{\rm \odot}}}$
is the Sun's mass-loss rate. In general, the mass-loss rate displays a complex empirical dependence on stellar parameters, for instance the star's mass, activity, age and rotation rate (Cranmer & Saar Reference Cranmer and Saar2011). We shall adopt the scaling relation proposed in Johnstone et al. (Reference Johnstone, Güdel, Brott and Lüftinger2015) for low-mass stars (although its validity remains somewhat uncertain for
${\dot {{\hskip4pt}M_{\rm \odot}}}$
is the Sun's mass-loss rate. In general, the mass-loss rate displays a complex empirical dependence on stellar parameters, for instance the star's mass, activity, age and rotation rate (Cranmer & Saar Reference Cranmer and Saar2011). We shall adopt the scaling relation proposed in Johnstone et al. (Reference Johnstone, Güdel, Brott and Lüftinger2015) for low-mass stars (although its validity remains somewhat uncertain for
![]() $M_{\rm \star} \lt 0.4M_{\rm \odot} $
and
$M_{\rm \star} \lt 0.4M_{\rm \odot} $
and
![]() $M_{\rm \star} \gt 1.1M_{\rm \odot} $
):
$M_{\rm \star} \gt 1.1M_{\rm \odot} $
):
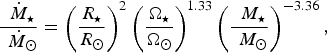 $$\displaystyle{\dot {{\hskip4pt}M_{\rm \star}} \over \dot {{\hskip4pt}M_{\rm \odot}}} = \left( {\displaystyle{{R_{\rm \star}} \over {R_{\rm \odot}}}} \right)^2 \left( {\displaystyle{{\Omega _{\rm \star}} \over {\Omega _{\rm \odot}}}} \right)^{1.33} \left( {\displaystyle{ {{\hskip4pt}M_{\rm \star}} \over {{\hskip4pt}M_{\rm \odot}}}} \right)^{ - 3.36}, $$
$$\displaystyle{\dot {{\hskip4pt}M_{\rm \star}} \over \dot {{\hskip4pt}M_{\rm \odot}}} = \left( {\displaystyle{{R_{\rm \star}} \over {R_{\rm \odot}}}} \right)^2 \left( {\displaystyle{{\Omega _{\rm \star}} \over {\Omega _{\rm \odot}}}} \right)^{1.33} \left( {\displaystyle{ {{\hskip4pt}M_{\rm \star}} \over {{\hskip4pt}M_{\rm \odot}}}} \right)^{ - 3.36}, $$
where
![]() $R_{\rm \star} $
,
$R_{\rm \star} $
,
![]() $\Omega _{\rm \star} $
and
$\Omega _{\rm \star} $
and
![]() $M_{\rm \star} $
are the stellar radius, rotation rate and mass, respectively. When we substitute the values for Proxima Centauri, we find that
$M_{\rm \star} $
are the stellar radius, rotation rate and mass, respectively. When we substitute the values for Proxima Centauri, we find that
![]() ${\hskip-4pt}\dot {{\hskip4pt}M_{\rm \star}} \approx 4.8 {\hskip-4pt}\dot {{\hskip4pt}M_{\rm \odot}} $
, which is fairly close to
${\hskip-4pt}\dot {{\hskip4pt}M_{\rm \star}} \approx 4.8 {\hskip-4pt}\dot {{\hskip4pt}M_{\rm \odot}} $
, which is fairly close to
![]() ${\hskip-4pt}\dot {{\hskip4pt}M_{\rm \star}} \approx {\hskip-4pt}\dot {{\hskip4pt}M_{\rm \odot}} $
obtained from simulations (Garraffo et al.
Reference Garraffo, Drake and Cohen2016). The above expression is based on the assumption that the star does not rotate rapidly,Footnote
7
since the mass-loss rate would otherwise attain a saturation value with the dependence
${\hskip-4pt}\dot {{\hskip4pt}M_{\rm \star}} \approx {\hskip-4pt}\dot {{\hskip4pt}M_{\rm \odot}} $
obtained from simulations (Garraffo et al.
Reference Garraffo, Drake and Cohen2016). The above expression is based on the assumption that the star does not rotate rapidly,Footnote
7
since the mass-loss rate would otherwise attain a saturation value with the dependence
![]() ${\hskip-4pt}\dot {{\hskip4pt}M_{\rm \star}} \propto M_{\rm \star}^{1.3}$
in that regime (Johnstone et al.
Reference Johnstone, Güdel, Brott and Lüftinger2015).
${\hskip-4pt}\dot {{\hskip4pt}M_{\rm \star}} \propto M_{\rm \star}^{1.3}$
in that regime (Johnstone et al.
Reference Johnstone, Güdel, Brott and Lüftinger2015).
A few general observations can be drawn from equations (9) and (10). The likelihood function is linearly proportional to the surface pressure (which itself is related to M
atm), implying that planets with relatively massive atmospheres are conducive to being superhabitable, in agreement with Vladilo et al. (Reference Vladilo, Murante, Silva, Provenzale, Ferri and Ragazzini2013) and Heller & Armstrong (Reference Heller and Armstrong2014). Secondly, we observe that exoplanets in the HZ around M-dwarfs are typically subject to higher values of 〈F
EUV〉 compared with the Earth (France et al.
Reference France2013), and are also located much closer (Kopparapu et al.
Reference Kopparapu, Ramirez, Kasting, Eymet, Robinson, Mahadevan, Terrien, Domagal-Goldman, Meadows and Deshpande2013). When combined with equations (9) and (10), these facts imply that
![]() ${ {\cal P}}_{\rm A} $
for such exoplanets is likely to be much lower than unity.
${ {\cal P}}_{\rm A} $
for such exoplanets is likely to be much lower than unity.
We have seen that t ℓ quantifies the timescale over which the atmosphere is present. Over this duration, it is worth highlighting that species diversity itself increases over time. The enhancement of biodiversity has been predicted to obey logistic growth (Purvis & Hector Reference Purvis and Hector2000; Benton Reference Benton2009), which can, in some instances, be loosely visualized as a linear function during the growing phase prior to saturation. Thus, one could, perhaps, also envision equation (8) as a heuristic measure of the maximal species diversity relative to Earth. In turn, a planetary ecosystem with higher biodiversity would be typically associated with greater stability and multifunctionality (Hooper et al. Reference Hooper2005; Cardinale et al. Reference Cardinale2012), although the subtleties inherent in analyses of diversity–stability relationships should be duly recognized (Ives & Carpenter Reference Ives and Carpenter2007).
Lastly, we observe that
![]() ${ {\cal P}}_{\rm A} = 0$
when t
ℓ < t
OOL since the planet's atmosphere is lost prior to the onset of abiogenesis. Similarly, if t
ℓ > t
HZ : = t
IHZ − t
OHZ, one must replace t
ℓ in equation (8) with t
HZ since the latter would become the critical timescale in this regime.
${ {\cal P}}_{\rm A} = 0$
when t
ℓ < t
OOL since the planet's atmosphere is lost prior to the onset of abiogenesis. Similarly, if t
ℓ > t
HZ : = t
IHZ − t
OHZ, one must replace t
ℓ in equation (8) with t
HZ since the latter would become the critical timescale in this regime.
The likelihood function and its consequences
We are now in a position to define the overall likelihood function
![]() ${ {\cal P}}$
from the preceding results,
${ {\cal P}}$
from the preceding results,
where
![]() ${ {\cal P}}_{\rm T} $
is given by equation (4) and
${ {\cal P}}_{\rm T} $
is given by equation (4) and
![]() ${ {\cal P}}_{\rm A} $
corresponds to either equation (9) or equation (10) depending on the dominant process that drives atmospheric escape.
${ {\cal P}}_{\rm A} $
corresponds to either equation (9) or equation (10) depending on the dominant process that drives atmospheric escape.
This function can be used to determine the likelihood of a planet being conducive to life relative to Earth. The chief advantage of our methodology is that nearly all of the parameters are direct observables, or can be deduced indirectly, by means of numerical simulations. The two primary uncertainties involve the surface pressure P s and the surface temperature T. In our subsequent analysis, we shall suppose that the surface pressure is equal to that of the Earth. This still leaves us with δ, which is defined in equation (5). We introduce the ansatz T = ζT eq, where T eq is the equilibrium temperature and ζ is a phenomenological parameter that captures the effects of greenhouse warming, snowball dynamics, tidal heating and other feedback mechanisms. In general, ζ is not constant across all planets, but we adopt this simplifying assumption in order to derive the likelihood function for some of the recently discovered exoplanets in Table 1.
Table 1. The likelihood function relative to Earth for different HZ exoplanets

![]() ${ {\cal P}}_{\rm A} ({\rm HD})$
and
${ {\cal P}}_{\rm A} ({\rm HD})$
and
![]() ${ {\cal P}}_{\rm A} ({\rm SW})$
are given by equations (9) and (10), respectively, while
${ {\cal P}}_{\rm A} ({\rm SW})$
are given by equations (9) and (10), respectively, while
![]() ${{\cal P}}({\rm HD}) = { {\cal P}}_{\rm T} \cdot { {\cal P}}_{\rm A} ({\rm HD})$
and
${{\cal P}}({\rm HD}) = { {\cal P}}_{\rm T} \cdot { {\cal P}}_{\rm A} ({\rm HD})$
and
![]() ${ {\cal P}}({\rm SW}) = { {\cal P}}_{\rm T} \cdot { {\cal P}}_{\rm A} ({\rm SW})$
. The stellar mass-loss rate for Proxima Centauri is from Garraffo et al. (Reference Garraffo, Drake and Cohen2016) (see also Wood et al.
Reference Wood, Linsky, Müller and Zank2001) and the corresponding value for TRAPPIST-1 has been assumed to be approximately equal to that of Proxima Centauri. The stellar and planetary parameters have been tabulated in Anglada-Escudé et al. (Reference Anglada-Escudé2016) and Gillon et al. (Reference Gillon2017), while EUV fluxes were taken from Ribas et al. (Reference Ribas2016) and Bourrier et al. (Reference Bourrier, Ehrenreich, Wheatley, Bolmont, Gillon, de Wit, Burgasser, Jehin, Queloz and Triaud2017) (see also Bolmont et al.
Reference Bolmont, Selsis, Owen, Ribas, Raymond, Leconte and Gillon2017) for Proxima b and the TRAPPIST-1 system, respectively.
${ {\cal P}}({\rm SW}) = { {\cal P}}_{\rm T} \cdot { {\cal P}}_{\rm A} ({\rm SW})$
. The stellar mass-loss rate for Proxima Centauri is from Garraffo et al. (Reference Garraffo, Drake and Cohen2016) (see also Wood et al.
Reference Wood, Linsky, Müller and Zank2001) and the corresponding value for TRAPPIST-1 has been assumed to be approximately equal to that of Proxima Centauri. The stellar and planetary parameters have been tabulated in Anglada-Escudé et al. (Reference Anglada-Escudé2016) and Gillon et al. (Reference Gillon2017), while EUV fluxes were taken from Ribas et al. (Reference Ribas2016) and Bourrier et al. (Reference Bourrier, Ehrenreich, Wheatley, Bolmont, Gillon, de Wit, Burgasser, Jehin, Queloz and Triaud2017) (see also Bolmont et al.
Reference Bolmont, Selsis, Owen, Ribas, Raymond, Leconte and Gillon2017) for Proxima b and the TRAPPIST-1 system, respectively.
We find that the likelihood function
![]() ${ {\cal P}}_{\rm A} $
for Proxima b and TRAPPIST-1e is about 1–2 orders of magnitude lower than that of Earth if the atmospheric escape is dominated by hydrodynamic escape. If the atmospheric losses occur due to stellar wind erosion, we conclude that the likelihood is even lower (by three orders of magnitude) for these planets. Another interesting result is that TRAPPIST-1e exhibits a higher likelihood of being habitable (albeit by only a factor of a few) when compared with Proxima b. When dealing with Proxima b, the ostensibly habitable planets of the TRAPPIST-1 system, and other exoplanets in the HZ of M-dwarfs, it is equally important to realize that the timescales for atmospheric loss may be sufficiently short such that t
ℓ<t
OOL, thereby implying that abiogenesis will be non-functional on these planets.
${ {\cal P}}_{\rm A} $
for Proxima b and TRAPPIST-1e is about 1–2 orders of magnitude lower than that of Earth if the atmospheric escape is dominated by hydrodynamic escape. If the atmospheric losses occur due to stellar wind erosion, we conclude that the likelihood is even lower (by three orders of magnitude) for these planets. Another interesting result is that TRAPPIST-1e exhibits a higher likelihood of being habitable (albeit by only a factor of a few) when compared with Proxima b. When dealing with Proxima b, the ostensibly habitable planets of the TRAPPIST-1 system, and other exoplanets in the HZ of M-dwarfs, it is equally important to realize that the timescales for atmospheric loss may be sufficiently short such that t
ℓ<t
OOL, thereby implying that abiogenesis will be non-functional on these planets.
When we consider TRAPPIST-1f and TRAPPIST-1g, the overall likelihood function ends up being zero in our simplified model because
![]() ${ {\cal P}}_{\rm T} = 0$
for T <T
L. We reiterate that this only represents a coarse-grained, global likelihood; in reality, there may exist locally favourable temperatures, perhaps near the terminator line, for these two planets enabling
${ {\cal P}}_{\rm T} = 0$
for T <T
L. We reiterate that this only represents a coarse-grained, global likelihood; in reality, there may exist locally favourable temperatures, perhaps near the terminator line, for these two planets enabling
![]() ${ {\cal P}}_{\rm T} \ne 0$
to occur in these regions. Our conclusions pertaining to these two planets are also broadly consistent with the results obtained from three-dimensional climate simulations (Wolf Reference Wolf2017), although the latter study (as well as our model) does not include the effects of tidal heating that are likely to be significant in the TRAPPIST-1 exoplanetary system.
${ {\cal P}}_{\rm T} \ne 0$
to occur in these regions. Our conclusions pertaining to these two planets are also broadly consistent with the results obtained from three-dimensional climate simulations (Wolf Reference Wolf2017), although the latter study (as well as our model) does not include the effects of tidal heating that are likely to be significant in the TRAPPIST-1 exoplanetary system.
In Fig. 1, we plot
![]() ${ {\cal P}}_{\rm T} $
, given by equation (4), as a function of the planet's surface temperature T. This plot can be interpreted as the likelihood of the Earth sustaining a complex biosphere provided that it was characterized by a steady surface temperature different from its current value. The presence of the exponential function ensures that the likelihood can vary over two orders of magnitude for a relatively narrow range of T. This serves to underscore the fact that a variety of macroecological processes are quite sensitive to the temperature, implying that the latter parameter will clearly play a central role in discussions of planetary habitability.
${ {\cal P}}_{\rm T} $
, given by equation (4), as a function of the planet's surface temperature T. This plot can be interpreted as the likelihood of the Earth sustaining a complex biosphere provided that it was characterized by a steady surface temperature different from its current value. The presence of the exponential function ensures that the likelihood can vary over two orders of magnitude for a relatively narrow range of T. This serves to underscore the fact that a variety of macroecological processes are quite sensitive to the temperature, implying that the latter parameter will clearly play a central role in discussions of planetary habitability.
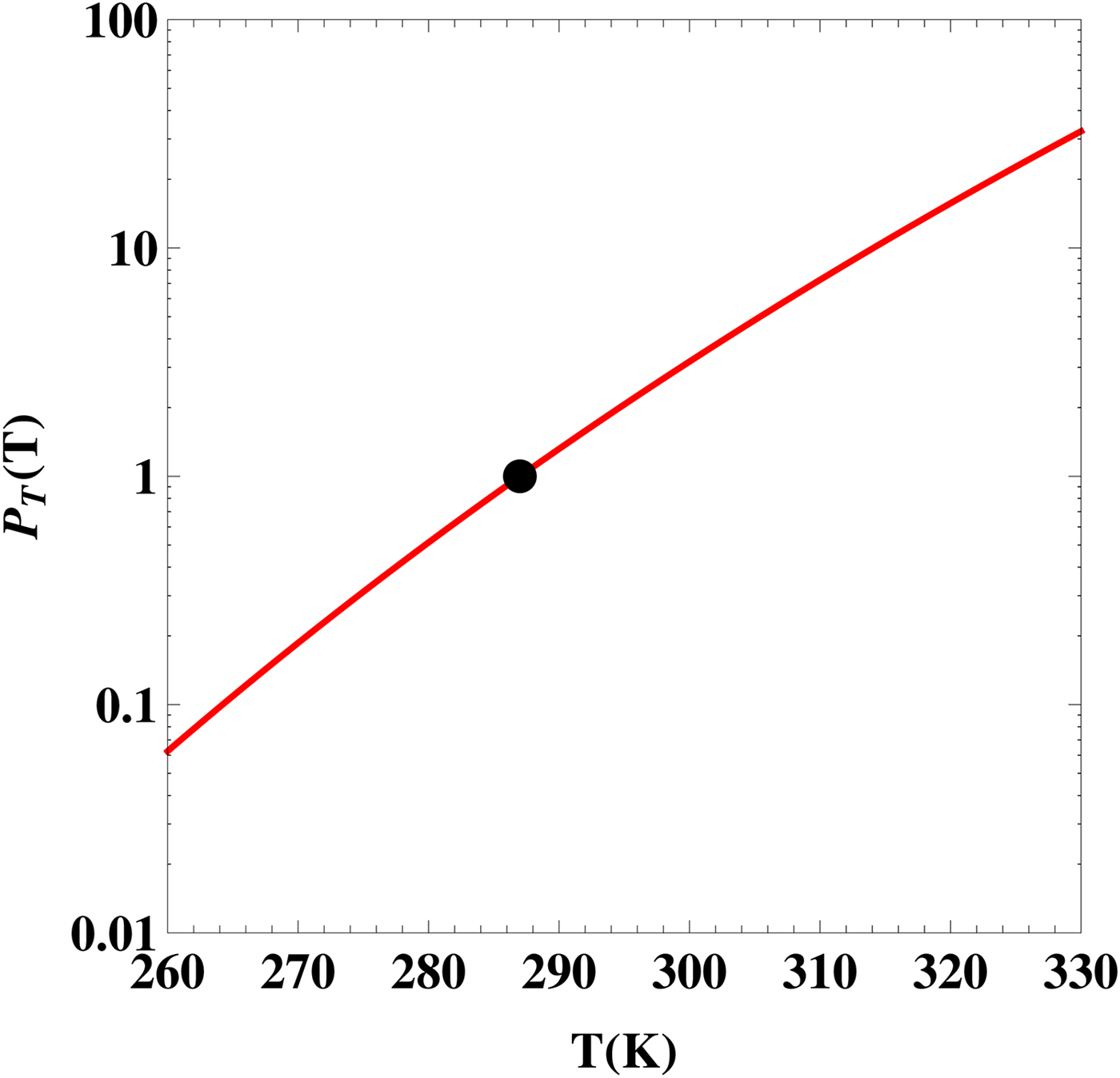
Fig. 1. The likelihood as a function of the planet's average surface temperature T. The black dot represents the Earth's value at T = 287 K.
Upon inspecting equation (9) next, we find that it depends on both planetary and stellar parameters. We shall focus on planets that are ‘Earth-like’ (but only in a superficial sense), i.e. the surface pressure and radius are chosen to equal the Earth's values. Figure 2 depicts the plot of
![]() ${ {\cal P}}_{\rm A} ({\rm HD})$
as a function of 〈F
EUV〉. Physically speaking, this figure quantifies the likelihood function of energy-limited atmospheric escape if the Earth were subjected to varying degrees of EUV flux.
${ {\cal P}}_{\rm A} ({\rm HD})$
as a function of 〈F
EUV〉. Physically speaking, this figure quantifies the likelihood function of energy-limited atmospheric escape if the Earth were subjected to varying degrees of EUV flux.
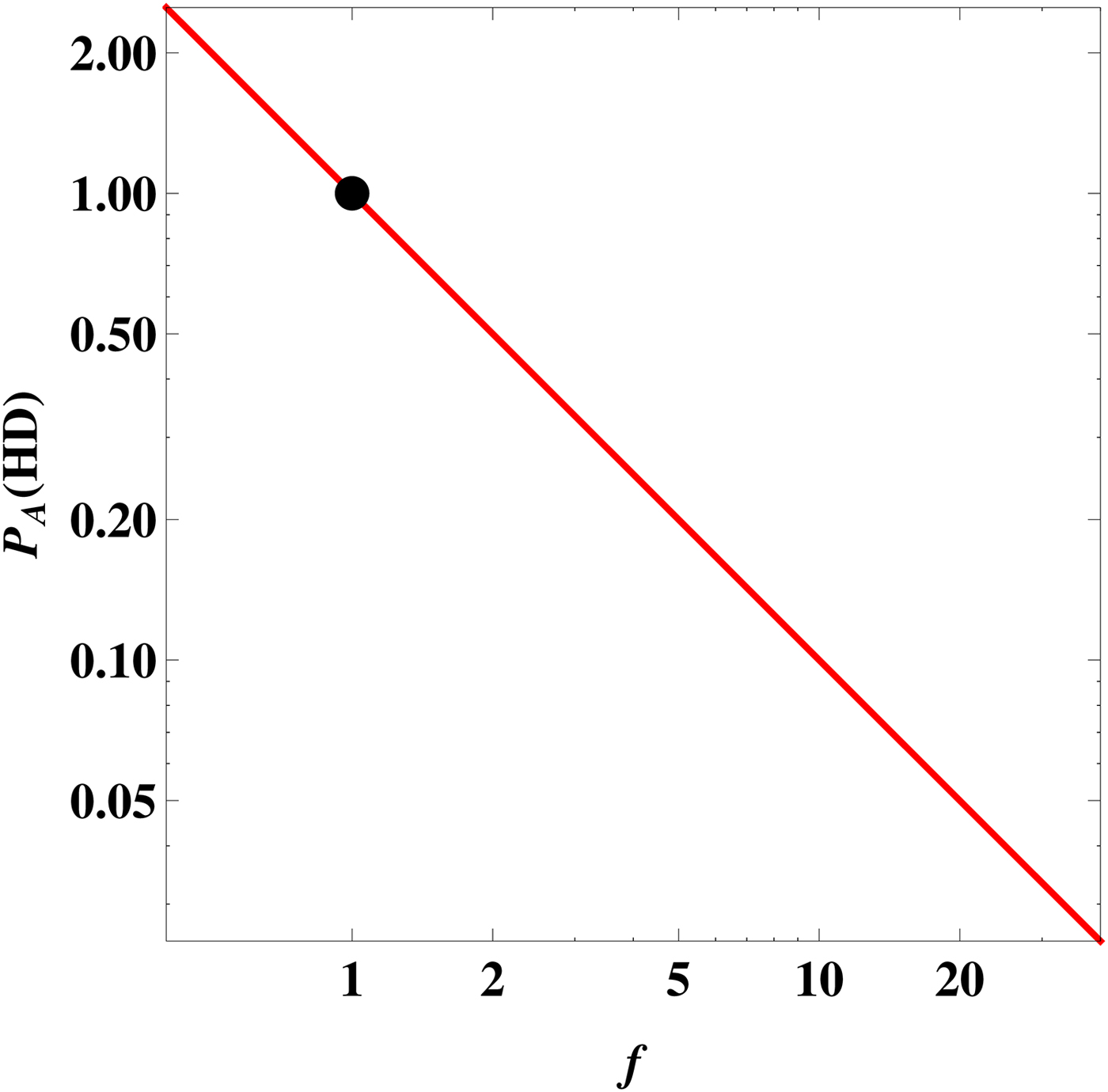
Fig. 2. The likelihood as a function of the normalized EUV flux
![]() $f = \langle F_{{\rm EUV}} \rangle /\langle F_ \oplus \rangle $
for an Earth clone. The black dot represents the Earth's position at f = 1.
$f = \langle F_{{\rm EUV}} \rangle /\langle F_ \oplus \rangle $
for an Earth clone. The black dot represents the Earth's position at f = 1.
Finally, we turn our attention to equation (10). This equation involves a large number of planetary and stellar parameters as well. As before, we consider an ‘Earth clone’ with physical parameters equal to that of Earth, namely, P
s ~ 1 atm,
![]() $R_{\rm P} \,{\rm \sim}\, R_ \oplus $
and
$R_{\rm P} \,{\rm \sim}\, R_ \oplus $
and
![]() $T_{{\rm eq}} \,{\rm \sim}\, T_{{\rm eq}, \oplus} $
. If we further use
$T_{{\rm eq}} \,{\rm \sim}\, T_{{\rm eq}, \oplus} $
. If we further use
![]() $L_{\rm \star} \propto M_{\rm \star} ^3 $
(mass–luminosity relationship),
$L_{\rm \star} \propto M_{\rm \star} ^3 $
(mass–luminosity relationship),
![]() $R_{\rm \star} \propto M_{\rm \star} ^{0.8} $
(Johnstone et al.
Reference Johnstone, Güdel, Brott and Lüftinger2015) and
$R_{\rm \star} \propto M_{\rm \star} ^{0.8} $
(Johnstone et al.
Reference Johnstone, Güdel, Brott and Lüftinger2015) and
![]() $a \propto L_{\rm \star} ^{1/2} $
for a fixed value of T
eq and the Bond albedo, we end up with the scalings,
$a \propto L_{\rm \star} ^{1/2} $
for a fixed value of T
eq and the Bond albedo, we end up with the scalings,
 $${ {\cal P}}_{\rm A} ({\rm SW}) \approx \left( {\displaystyle{{\Omega _{\rm \star}} \over {\Omega _{\rm \odot}}}} \right)^{ - 1.33} \left( {\displaystyle{{M_{\rm \star}} \over {M_{\rm \odot}}}} \right)^{4.76}, $$
$${ {\cal P}}_{\rm A} ({\rm SW}) \approx \left( {\displaystyle{{\Omega _{\rm \star}} \over {\Omega _{\rm \odot}}}} \right)^{ - 1.33} \left( {\displaystyle{{M_{\rm \star}} \over {M_{\rm \odot}}}} \right)^{4.76}, $$
for the likelihood of the Earth's atmosphere to persist – which is a necessary although not sufficient condition for habitability – in the HZ of a different star. Thus, we can immediately see that a slowly rotating, higher mass star is more conducive to hosting life on an Earth clone. Note that the above formula is not valid for rapidly rotating stars that yield scaling relations different from the Sun; a similar analysis using the corresponding formula for
![]() ${\hskip-4pt}\dot {{\hskip4pt}M_{\rm \star}} $
from Johnstone et al. (Reference Johnstone, Güdel, Brott and Lüftinger2015) leads to,
${\hskip-4pt}\dot {{\hskip4pt}M_{\rm \star}} $
from Johnstone et al. (Reference Johnstone, Güdel, Brott and Lüftinger2015) leads to,
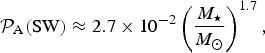 $${ {\cal P}}_{\rm A} ({\rm SW}) \approx 2.7 \times 10^{ - 2} \left( {\displaystyle{{M_{\rm \star}} \over {M_{\rm \odot}}}} \right)^{1.7}, $$
$${ {\cal P}}_{\rm A} ({\rm SW}) \approx 2.7 \times 10^{ - 2} \left( {\displaystyle{{M_{\rm \star}} \over {M_{\rm \odot}}}} \right)^{1.7}, $$
which does not exhibit an
![]() $\Omega _{\rm \star} $
dependence. This expression also implies that stars with a higher mass are more likely to host planets in the HZ that are capable of possessing long-term atmospheres.Footnote
8
We reiterate that equations (13) and (14) are only valid for an Earth clone, and, in reality,
$\Omega _{\rm \star} $
dependence. This expression also implies that stars with a higher mass are more likely to host planets in the HZ that are capable of possessing long-term atmospheres.Footnote
8
We reiterate that equations (13) and (14) are only valid for an Earth clone, and, in reality,
![]() ${ {\cal P}}_{\rm A} ({\rm SW})$
depends both on stellar and planetary parameters as seen from equation (10). We have plotted the results from equations (13) and (14) in the two panels of Fig. 3.
${ {\cal P}}_{\rm A} ({\rm SW})$
depends both on stellar and planetary parameters as seen from equation (10). We have plotted the results from equations (13) and (14) in the two panels of Fig. 3.
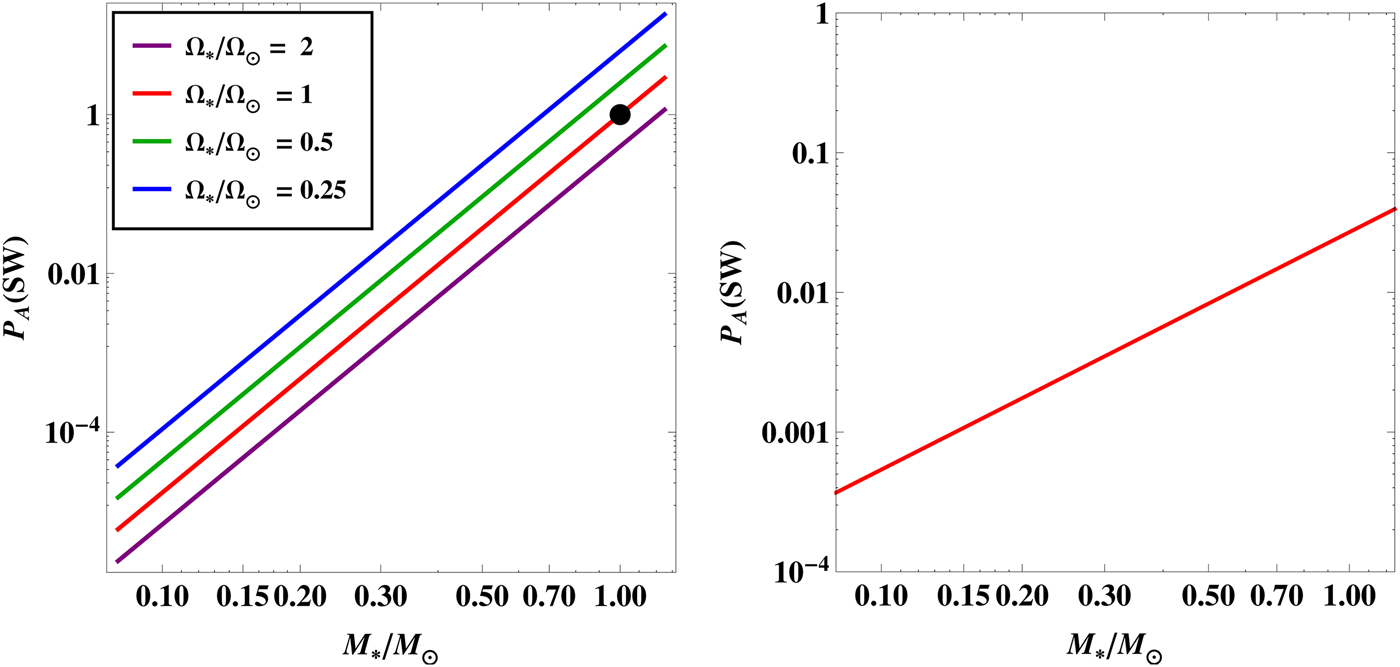
Fig. 3. The likelihood as a function of the stellar mass for an Earth clone. In the left-hand panel, each plot corresponds to a different value of the rotation rate
![]() $\Omega _{\rm \star} $
. The black dot signifies the position of the Sun. In the right-hand panel, the likelihood has been plotted for rapidly rotating stars, in which case it does not depend on
$\Omega _{\rm \star} $
. The black dot signifies the position of the Sun. In the right-hand panel, the likelihood has been plotted for rapidly rotating stars, in which case it does not depend on
![]() $\Omega _{\rm \star} $
.
$\Omega _{\rm \star} $
.
Conclusions
In this paper, we have attempted to address the important question of habitability metrics from a more quantitative perspective. We begin with the caveat that our work entails a certain degree of terracentrism with an emphasis on life-as-we-know-it; the associated assumptions cannot be easily bypassed since the Earth is the only planet that is presently known to harbour life. In addition, a genuinely quantitative understanding of habitability is not feasible at this stage given that there exist far too many unknowns (Schulze-Makuch & Guinan Reference Schulze-Makuch and Guinan2016; Tasker et al. Reference Tasker2017).
We have attempted to: (i) draw upon models with strong physical underpinnings, and (ii) present the results in terms of basic physical parameters that can be determined via observations or simulations. We focused on two major physical processes, namely the role of planetary temperature and atmospheric escape. The former was analysed by means of the MTE, which predicts that many macroecological processes exhibit a Boltzmann factor dependence on the temperature within a certain range. We addressed the possibility of atmospheric escape by considering two different mechanisms, namely hydrodynamic escape and stellar wind-induced stripping.
Our analysis gave rise to a diverse array of conclusions, which have been summarized below:
-
• Planets with a warmer mean surface temperature are more conducive to being habitable, insofar macroscopic ecological (as well as evolutionary) processes are concerned, albeit only up to a limited temperature range.
-
• Planets with higher surface pressure are, ceteris paribus, more likely to be habitable.Footnote 9 It has also been argued by some authors that abiogenesis on Earth was initiated in a high-pressure environment (Martin et al. Reference Martin, Baross, Kelley and Russell2008; Picard & Daniel Reference Picard and Daniel2013), consequently indicating that pressure may play a potentially positive role in the OOL.
-
• For an ‘Earth clone’ around a different star, the likelihood of retaining its atmosphere increases with the star's mass, while decreasing with rotation rate and the average ultraviolet (EUV) flux. High doses of ionizing radiation are also likely to have deleterious effects on the functioning of organic molecules and organisms (Dartnell Reference Dartnell2011), although the beneficial effects of UV radiation in the context of prebiotic chemistry have been well documented (Ranjan & Sasselov Reference Ranjan and Sasselov2016).
-
• On account of the above reasons, Earth-sized planets in the HZ around M-dwarfs are presumably much less likely to be habitable, conceivably by several orders of magnitude, when compared with the Earth–Sun system. Hence, even though M-dwarfs outnumber other stars in our Galaxy, we propose that future searches for life on exo-Earths (Horner & Jones Reference Horner and Jones2010) should prioritize a subset of G- and K-type stars (Tian & Ida Reference Tian and Ida2015; Cuntz & Guinan Reference Cuntz and Guinan2016). This may also explain why we live on a terrestrial planet currently in the HZ of the Sun, and not one that is in the HZ of an M-dwarf in the cosmic future (Loeb et al. Reference Loeb, Batista and Sloan2016; Haqq-Misra et al. Reference Haqq-Misra, Kopparapu and Wolf2017).
-
• More specifically, Proxima b and TRAPPIST-1e yield a much lower likelihood of being habitable (by 2–4 orders of magnitude), with respect to atmospheric escape mechanisms, when compared with Earth. Furthermore, TRAPPIST-1e appears to be more conducive to hosting life, while only by a factor of a few, with respect to Proxima b if one makes the further assumption that their host stars have a similar stellar mass-loss rate.
-
• If the assumptions in this paper are valid, it seems plausible that TRAPPIST-1f and TRAPPIST-1g are incapable of sustaining life across a significant fraction of the surface, although the possibility of local life-bearing zones and life seeded by means of panspermia (Lingam Reference Lingam2016; Lingam & Loeb Reference Lingam and Loeb2017) cannot and ought not be ruled out.
-
• As most of the stellar and planetary parameters are time-dependent, the likelihood functions are also implicitly dynamical.Footnote 10 This fact is fully consistent with the notion that planetary habitability (and sustainability) evolves over time (Frank & Sullivan Reference Frank and Sullivan2014).
-
• Many of these findings, after suitable reinterpretation, are also applicable to habitable exomoons, which may outnumber habitable exoplanets (Heller et al. Reference Heller2014).
We end by cautioning that our proposed methodology is by no means complete, since important (first-order) feedback mechanisms – such as the complex, non-linear and adaptive interplay between life and planetary habitability (Levins Reference Levins1968; Lovelock & Margulis Reference Lovelock and Margulis1974; Levin Reference Levin1998; Angeli et al.
Reference Angeli, Ferrell and Sontag2004; Chopra & Lineweaver Reference Chopra and Lineweaver2016) – have not been included herein (Lineweaver & Chopra Reference Lineweaver and Chopra2012; Ehlmann et al.
Reference Ehlmann2016; Judson Reference Judson2017). We also wish to point out that we have altogether neglected second-order effects in this study. For instance, it has been suggested that a larger surface area facilitates higher biodiversity (Rosenzweig Reference Rosenzweig1995), thereby making the planet superhabitable (Heller & Armstrong Reference Heller and Armstrong2014). However, it is important to recognize that the radius (and hence the area) of super-Earths is quite constrained (Rogers Reference Rogers2015; Chen & Kipping Reference Chen and Kipping2017), thereby implying that this effect qualifies as an
![]() ${ {\cal O}}(1)$
contribution.
${ {\cal O}}(1)$
contribution.
As our work is founded on physical and mechanistic considerations inclined towards universality, we advocate the adoption of such an approach in future studies that seek to quantify the likelihood of exoplanets hosting complex and long-lived biospheres. Pursuing such lines of enquiry may also prove to be a natural and timely means of investigating the dependence of abiogenesis, at least for life-as-we-know-it, on biochemical (possibly even planetary and stellar) parameters by means of associated paradigms (Goldenfeld & Woese Reference Goldenfeld and Woese2011; Pascal et al. Reference Pascal, Pross and Sutherland2013; Davies & Walker Reference Davies and Walker2016), thereby complementing previous probabilistic estimates (Lineweaver & Davis Reference Lineweaver and Davis2002; Carter Reference Carter2008; Spiegel & Turner Reference Spiegel and Turner2012; Scharf & Cronin Reference Scharf and Cronin2016). Studies along these lines would lead us towards a resolution of the fundamental question as to whether life (and intelligence) in the universe is an extremely rare phenomenon (Simpson Reference Simpson1964; Monod Reference Monod1971; Ward & Brownlee Reference Ward and Brownlee2000; Morris Reference Morris2003) or an inevitable ‘cosmic imperative’ (de Duve Reference de Duve1995, Reference de Duve2011).Footnote 11
Acknowledgements
The authors thank Chuanfei Dong, John Forbes, Jeffrey Linsky, Sukrit Ranjan, John Raymond, Ed Turner and the referee for their helpful comments concerning the paper. This work was supported in part by a grant from the Breakthrough Prize Foundation for the Starshot Initiative.





