Hostname: page-component-7bb8b95d7b-w7rtg Total loading time: 0 Render date: 2024-10-03T23:41:46.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Local limit theorem for a Markov additive process on 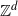$\mathbb{Z}^d$ with a null recurrent internal Markov chain

Part of: Markov processes Special processes Limit theorems

Published online by Cambridge University Press:  22 December 2022

Basile de Loynes Open the ORCID record for Basile de Loynes [Opens in a new window]
Basile de Loynes*
Affiliation:
CREST-ENSAI
*
*Postal address: Campus de Ker-Lann, Rue Blaise Pascal, BP 37203, 35172 Bruz Cedex. Email: bdeloynes@math.cnrs.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In the classical framework, a random walk on a group is a Markov chain with independent and identically distributed increments. In some sense, random walks are time and space homogeneous. This paper is devoted to a class of inhomogeneous random walks on 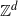$\mathbb{Z}^d$ termed ‘Markov additive processes’ (also known as Markov random walks, random walks with internal degrees of freedom, or semi-Markov processes). In this model, the increments of the walk are still independent but their distributions are dictated by a Markov chain, termed the internal Markov chain. While this model is largely studied in the literature, most of the results involve internal Markov chains whose operator is quasi-compact. This paper extends two results for more general internal operators: a local limit theorem and a sufficient criterion for their transience. These results are thereafter applied to a new family of models of drifted random walks on the lattice $\mathbb{Z}^d$ .

Keywords

Inhomogeneous random walkssemi-Markov processesMarkov random walksrandom walks with internal degrees of freedomrecurrencetransienceFourier analysis

MSC classification

Primary: 60F15: Strong theorems 60K15: Markov renewal processes, semi-Markov processes
Secondary: 60J45: Probabilistic potential theory 60J10: Markov chains (discrete-time Markov processes on discrete state spaces) 60J55: Local time and additive functionals
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 2 , June 2023 , pp. 570 - 588
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alsmeyer, G. (2001). Recurrence theorems for Markov random walks. Prob. Math. Statist. 21, 123–134.Google Scholar
Babillot, M. (1988). Théorie du renouvellement pour des chanes semi-markoviennes transientes. Ann. Inst. H. Poincaré Prob. Statist. 24, 507–569.Google Scholar
Bartholdi, L. and Erschler, A. (2017). Poisson–Furstenberg boundary and growth of groups. Prob. Theory Relat. Fields 168, 347–372.CrossRefGoogle Scholar
Bartholdi, L. and Virág, B. (2005). Amenability via random walks. Duke Math. J. 130, 39–56.CrossRefGoogle Scholar
Benjamini, I., Kozma, G. and Schapira, B. (2011). A balanced excited random walk. C. R. Math. Acad. Sci. Paris 349, 459–462.CrossRefGoogle Scholar
Blachère, S., Hassinsky, P. and Mathieu, P. (2008). Asymptotic entropy and Green speed for random walks on countable groups. Ann. Prob. 36, 1134–1152.CrossRefGoogle Scholar
Bosi, G., Hu, Y. and Peres, Y. (2022). Recurrence and windings of two revolving random walks. Electron. J. Prob. 27, 66.CrossRefGoogle Scholar
Brémont, J. (2016). On planar random walks in environments invariant by horizontal translations. Markov Process. Relat. Fields 22, 267–309.Google Scholar
Brémont, J. (2017). Markov chains in a stratified environment. ALEA Lat. Am. J. Prob. Math. Stat. 14, 751–798.CrossRefGoogle Scholar
Brémont, J. (2021). Planar random walk in a stratified quasi-periodic environment. Markov Process. Relat. Fields 27, 755–788.Google Scholar
Brofferio, S. and Woess, W. (2005). Green kernel estimates and the full Martin boundary for random walks on lamplighter groups and Diestel–Leader graphs. Ann. Inst. H. Poincaré Prob. Statist. 41, 1101–1123.CrossRefGoogle Scholar
Campanino, M. and Petritis, D. (2003). Random walks on randomly oriented lattices. Markov Process. Relat. Fields 9, 391–412.Google Scholar
Campanino, M. and Petritis, D. (2014). Type transition of simple random walks on randomly directed regular lattices. J. Appl. Prob. 51, 1065–1080.CrossRefGoogle Scholar
Castell, F., Guillotin-Plantard, N., Pène, F. and Schapira, B. (2011). A local limit theorem for random walks in random scenery and on randomly oriented lattices. Ann. Prob. 39, 2079–2118.CrossRefGoogle Scholar
Çinlar, E. (1972). Markov additive processes. I. Z. Wahrscheinlichkeitsth. 24, 85–93.CrossRefGoogle Scholar
Çinlar, E. (1972). Markov additive processes. II. Z. Wahrscheinlichkeitsth. 24, 95–121.CrossRefGoogle Scholar
Cénac, P., Chauvin, B., Herrmann, S. and Vallois, P. (2013). Persistent random walks, variable length Markov chains and piecewise deterministic Markov processes. Markov Process. Relat. Fields 19, 1–50.Google Scholar
Cénac, P., Chauvin, B., Paccaut, F. and Pouyanne, N. (2012). Context trees, variable length Markov chains and dynamical sources. In Séminaire de Probabilités XLIV, eds Donati-Martin, C., Lejay, A. and Rouault, A. (Lecture Notes Math. 2046). Springer, Heidelberg, pp. 1–39.CrossRefGoogle Scholar
Cénac, P., de Loynes, B., Offret, Y. and Rousselle, A. (2020). Recurrence of multidimensional persistent random walks. Fourier and series criteria. Bernoulli 26, 858–892.CrossRefGoogle Scholar
Cénac, P., Le Ny, A., de Loynes, B. and Offret, Y. (2018). Persistent random walks. I. Recurrence versus transience. J. Theoret. Prob. 31, 232–243.CrossRefGoogle Scholar
Cénac, P., Le Ny, A., de Loynes, B. and Offret, Y. (2019). Persistent random walks. II. Functional scaling limits. J. Theoret. Prob. 32, 633–658.CrossRefGoogle Scholar
Chung, K. L. and Fuchs, W. H. J. (1951). On the distribution of values of sums of random variables. Mem. Amer. Math. Soc. 6, 12.Google Scholar
Comets, F., Menshikov, M. V., Volkov, S. and Wade, A. R. (2011). Random walk with barycentric self-interaction. J. Stat. Phys. 143, 855–888.CrossRefGoogle Scholar
de Loynes, B. (2012). Marche aléatoire sur un di-graphe et frontière de Martin. C. R. Math. Acad. Sci. Paris 350, 87–90.CrossRefGoogle Scholar
Dunford, N. and Schwartz, J. T. (1988). Linear operators. Part III. John Wiley, New York.Google Scholar
Ēžov, I. I. and Skorohod, A. V. (1969). Markov processes which are homogeneous in the second component. I. Teor. Veroyatn. Primen. 14, 3–14.Google Scholar
Ferré, D., Hervé, L. and Ledoux, J. (2012). Limit theorems for stationary Markov processes with $L^2$ -spectral gap. Ann. Inst. Henri Poincaré Prob. Statist. 48, 396–423.CrossRefGoogle Scholar
Fuh, C.-D. and Lai, T. L. (2001). Asymptotic expansions in multidimensional Markov renewal theory and first passage times for Markov random walks. Adv. Appl. Prob. 33, 652–673.CrossRefGoogle Scholar
Goldstein, L. and Reinert, G. (2013). Stein’s method for the beta distribution and the Pólya–Eggenberger urn. J. Appl. Prob. 50, 1187–1205.CrossRefGoogle Scholar
Gouëzel, S., Mathéus, F. and Maucourant, F. (2015). Sharp lower bounds for the asymptotic entropy of symmetric random walks. Groups Geom. Dyn. 9, 711–735.CrossRefGoogle Scholar
Guibourg, D. and Hervé, L. (2011). A renewal theorem for strongly ergodic Markov chains in dimension $d\geq 3$ and centered case. Potential Anal. 34, 385–410.CrossRefGoogle Scholar
Guibourg, D. and Hervé, L. (2013). Multidimensional renewal theory in the non-centered case. Application to strongly ergodic Markov chains. Potential Anal. 38, 471–497.CrossRefGoogle Scholar
Guillotin-Plantard, N. and Le Ny, A. (2007). Transient random walks on 2D-oriented lattices. Teor. Veroyatn. Primen. 52, 815–826.CrossRefGoogle Scholar
Guillotin-Plantard, N. and Le Ny, A. (2008). A functional limit theorem for a 2D-random walk with dependent marginals. Electron. Commun. Prob. 13, 337–351.CrossRefGoogle Scholar
Guivarc’h, Y. (1984). Application d’un théorème limite local à la transience et à la récurrence de marches de Markov. In Théorie du potentiel, eds Mokobodzki, G. and Pinchon, D. (Lecture Notes Math. 1096). Springer, Berlin, pp. 301–332.CrossRefGoogle Scholar
Guivarc’h, Y. and Raja, C. R. E. (2012). Recurrence and ergodicity of random walks on linear groups and on homogeneous spaces. Ergodic Theory Dynam. Systems 32, 1313–1349.CrossRefGoogle Scholar
Hervé, L. (2005). Théorème local pour chanes de Markov de probabilité de transition quasi-compacte. Applications aux chanes V-géométriquement ergodiques et aux modèles itératifs. Ann. Inst. H. Poincaré Prob. Statist. 41, 179–196.CrossRefGoogle Scholar
Hervé, L. and Ledoux, J. (2013). A local limit theorem for densities of the additive component of a finite Markov additive process. Statist. Prob. Lett. 83, 2119–2128.CrossRefGoogle Scholar
Hervé, L., Ledoux, J. and Patilea, V. (2012). A uniform Berry–Esseen theorem on M-estimators for geometrically ergodic Markov chains. Bernoulli 18, 703–734.CrossRefGoogle Scholar
Hervé, L. and Pène, F. (2010). The Nagaev–Guivarc’h method via the Keller–Liverani theorem. Bull. Soc. Math. France 138, 415–489.CrossRefGoogle Scholar
Hervé, L. and Pène, F. (2013). On the recurrence set of planar Markov random walks. J. Theoret. Prob. 26, 169–197.CrossRefGoogle Scholar
Kaimanovich, V. A. and Woess, W. (2002). Boundary and entropy of space homogeneous Markov chains. Ann. Prob. 30, 323–363.CrossRefGoogle Scholar
Karlsson, A. and Woess, W. (2007). The Poisson boundary of lamplighter random walks on trees. Geom. Dedicata 124, 95–107.CrossRefGoogle Scholar
Kato, T. (1995). Perturbation Theory for Linear Operators. Springer, Berlin.CrossRefGoogle Scholar
Kazami, T. and Uchiyama, K. (2008). Random walks on periodic graphs. Trans. Amer. Math. Soc. 360, 6065–6087.CrossRefGoogle Scholar
Kesten, H. (1974). Renewal theory for functionals of a Markov chain with general state space. Ann. Prob. 2, 355–386.CrossRefGoogle Scholar
Krámli, A. and Szász, D. (1983). Random walks with internal degrees of freedom. I. Local limit theorems. Z. Wahrscheinlichkeitsth. 63, 85–95.CrossRefGoogle Scholar
Lin, M. (1974). On quasi-compact Markov operators. Ann. Prob. 2, 464–475.CrossRefGoogle Scholar
Matheron, G. and De Marsily, G. (1980). Is transport in porous media always diffusive? A counterexample. Water Resources Research 16, 901–917.CrossRefGoogle Scholar
Mathieu, P. (2015). Differentiating the entropy of random walks on hyperbolic groups. Ann. Prob. 43, 166–187.CrossRefGoogle Scholar
Ney, P. and Nummelin, E. (1987). Markov additive processes. I. Eigenvalue properties and limit theorems. Ann. Prob. 15, 561–592.CrossRefGoogle Scholar
Ney, P. and Nummelin, E. (1987). Markov additive processes II. Large deviations. Ann. Prob. 15, 593–609.Google Scholar
Pemantle, R. (1992). Vertex-reinforced random walk. Prob. Theory Relat. Fields 92, 117–136.CrossRefGoogle Scholar
Pène, F. (2009). Transient random walk in $\mathbb{Z}^2$ with stationary orientations. ESAIM Prob. Stat. 13, 417–436.CrossRefGoogle Scholar
Peres, Y., Popov, S. and Sousi, P. (2013). On recurrence and transience of self-interacting random walks. Bull. Braz. Math. Soc. (N.S.) 44, 841–867.CrossRefGoogle Scholar
Pittet, C. and Saloff-Coste, L. (2002). On random walks on wreath products. Ann. Prob. 30, 948–977.CrossRefGoogle Scholar
Pólya, G. (1921). Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Straßennetz. Math. Ann. 84, 149–160.CrossRefGoogle Scholar
Raimond, O. and Schapira, B. (2010). Random walks with occasionally modified transition probabilities. Illinois J. Math. 54, 1213–1238.CrossRefGoogle Scholar
Rogers, L. C. G. (1985). Recurrence of additive functionals of Markov chains. Sankhyā A 47, 47–56.Google Scholar
Salaün, F. (2001). Marche aléatoire sur un groupe libre: théorèmes limite conditionnellement à la sortie. C. R. Acad. Sci. Paris Sér. I Math. 333, 359–362.CrossRefGoogle Scholar
Spitzer, F. (1976). Principles of Random Walk, 2nd edn (Grad. Texts Math. 34). Springer, New York.Google Scholar
Uchiyama, K. (2007). Asymptotic estimates of the Green functions and transition probabilities for Markov additive processes. Electron. J. Prob. 12, 138–180.CrossRefGoogle Scholar
Villani, C. (2009). Optimal Transport. Springer, Berlin.CrossRefGoogle Scholar
Volkov, S. (2001). Vertex-reinforced random walk on arbitrary graphs. Ann. Prob. 29, 66–91.CrossRefGoogle Scholar
Woess, W. (2000). Random walks on Infinite Graphs and Groups (Cambridge Tracts Math. 138). Cambridge University Press.Google Scholar