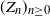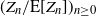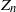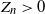1. Introduction and main results
Branching processes  $(Z_n)_{n \ge 0}$ in a varying environment generalize the classical Galton–Watson processes, in that they allow time dependence of the offspring distribution. This natural setting promises relevant applications (e.g. to random walks on trees, as in [Reference Lyons18]) and has recently received a renewal of interest, see e.g. [Reference Bansaye and Simatos2, Reference Braunsteins and Hautphenne4, Reference González, Kersting, Minuesa and del Puerto13, Reference Sagitov and Jagers20]. Former research on branching processes in a varying environment was temporarily affected by the appearence of certain exotic properties, and one could get the impression that it is difficult to grasp some kind of generic behaviour of these processes. Even so, steps in this direction were taken by Peter Jagers [Reference Jagers15]; in particular, he aimed for a classification into supercritical, critical and subcritical regimes in the spirit of ordinary Galton–Watson processes. In this paper we take up this line of research. To this end we prove several theorems reaching from criteria for almost sure extinction up to Yaglom-type results. We require only mild regularity assumptions, and in particular we set no restrictions on the sequence of expectations
$(Z_n)_{n \ge 0}$ in a varying environment generalize the classical Galton–Watson processes, in that they allow time dependence of the offspring distribution. This natural setting promises relevant applications (e.g. to random walks on trees, as in [Reference Lyons18]) and has recently received a renewal of interest, see e.g. [Reference Bansaye and Simatos2, Reference Braunsteins and Hautphenne4, Reference González, Kersting, Minuesa and del Puerto13, Reference Sagitov and Jagers20]. Former research on branching processes in a varying environment was temporarily affected by the appearence of certain exotic properties, and one could get the impression that it is difficult to grasp some kind of generic behaviour of these processes. Even so, steps in this direction were taken by Peter Jagers [Reference Jagers15]; in particular, he aimed for a classification into supercritical, critical and subcritical regimes in the spirit of ordinary Galton–Watson processes. In this paper we take up this line of research. To this end we prove several theorems reaching from criteria for almost sure extinction up to Yaglom-type results. We require only mild regularity assumptions, and in particular we set no restrictions on the sequence of expectations  $\mathrm E[Z_n]$,
$\mathrm E[Z_n]$,  $n \ge 0$, thereby generalizing and unifying a number of individual results from the literature.
$n \ge 0$, thereby generalizing and unifying a number of individual results from the literature.
In order to define a branching process in a varying environment (BPVE), let the sequence  $Y_1, Y_2, \ldots$ denote random variables with values in
$Y_1, Y_2, \ldots$ denote random variables with values in  $\mathbb N_0$, and
$\mathbb N_0$, and  $f_1,f_2, \ldots$ their distributions. Let
$f_1,f_2, \ldots$ their distributions. Let  $Y_{ni}$,
$Y_{ni}$,  $n,i\in \mathbb N$, be independent random variables such that
$n,i\in \mathbb N$, be independent random variables such that  $Y_{ni}$ and
$Y_{ni}$ and  $Y_n$ coincide in distribution for all
$Y_n$ coincide in distribution for all  $n,i\ge 1$. Define the random variables
$n,i\ge 1$. Define the random variables  $Z_n$,
$Z_n$,  $n \ge 0$, with values in
$n \ge 0$, with values in  $\mathbb N_0$ recursively as
$\mathbb N_0$ recursively as
 \[ Z_0 \,:\!=1, \quad Z_{n} \,:\!= \sum_{i=1}^{Z_{n-1}} Y_{ni}, \qquad n \ge 1 . \]
\[ Z_0 \,:\!=1, \quad Z_{n} \,:\!= \sum_{i=1}^{Z_{n-1}} Y_{ni}, \qquad n \ge 1 . \]
Then the process  $(Z_n)_{n \ge 0}$ is called a branching process in the varying environment
$(Z_n)_{n \ge 0}$ is called a branching process in the varying environment  $v=(\,f_1,f_2, \ldots\!)$with initial value
$v=(\,f_1,f_2, \ldots\!)$with initial value  $Z_0=1$. These processes may be considered as a model for the development of the size of a population where individuals reproduce independently with offspring distributions
$Z_0=1$. These processes may be considered as a model for the development of the size of a population where individuals reproduce independently with offspring distributions  $f_n$ potentially changing among generations. Without further mention we always require that
$f_n$ potentially changing among generations. Without further mention we always require that  $0 \lt \mathrm E[Y_n] \lt \infty$ for all
$0 \lt \mathrm E[Y_n] \lt \infty$ for all  $n \ge 1$.
$n \ge 1$.
There is one non-trivial statement on BPVEs requiring no extra assumption. It says that  $Z_n$ is almost surely (a.s.) convergent to a random variable
$Z_n$ is almost surely (a.s.) convergent to a random variable  $Z_\infty$ with values in
$Z_\infty$ with values in  $\mathbb N_0\cup \{\infty\}$. This result is due to Lindvall [Reference Lindvall17] and extends results of Church [Reference Church5] (for a comparatively short proof see [Reference Kersting and Vatutin14, Theorem 1.4]). It also clarifies under which conditions
$\mathbb N_0\cup \{\infty\}$. This result is due to Lindvall [Reference Lindvall17] and extends results of Church [Reference Church5] (for a comparatively short proof see [Reference Kersting and Vatutin14, Theorem 1.4]). It also clarifies under which conditions  $(Z_n)_{n \ge 0}$ may ‘fall asleep’ at a positive state, meaning that the event
$(Z_n)_{n \ge 0}$ may ‘fall asleep’ at a positive state, meaning that the event  $\{0 \lt Z_\infty \lt \infty\}$ occurs with positive probability. Let us call such a branching process asymptotically degenerate. Thus, for a BPVE it is no longer true that the process either gets extinct a.s. or else converges a.s. to infinity.
$\{0 \lt Z_\infty \lt \infty\}$ occurs with positive probability. Let us call such a branching process asymptotically degenerate. Thus, for a BPVE it is no longer true that the process either gets extinct a.s. or else converges a.s. to infinity.
As mentioned above, a BPVE may exhibit extraordinary properties that do not show up for ordinary Galton–Watson processes. Thus a BPVE may possess different growth rates, as detected by MacPhee and Schuh [Reference MacPhee and Schuh19]. Here we establish a framework which excludes such exceptional phenomena and elucidates the generic behaviour. As we shall see, this is naturally done in an  $\mathcal L^2$ setting.
$\mathcal L^2$ setting.
Our main assumption is a uniformity requirement which reads as follows. There is a constant  $c<\infty$ such that for all natural numbers
$c<\infty$ such that for all natural numbers  $n \ge 1$ we have
$n \ge 1$ we have
 \begin{align}\mathrm E[Y_n^2;\, Y_n \ge 2] \le c\, \mathrm E[Y_n;\, Y_n \ge 2] \cdot\mathrm E[Y_{n} \mid Y_n \ge 1]. \tag{A}\end{align}
\begin{align}\mathrm E[Y_n^2;\, Y_n \ge 2] \le c\, \mathrm E[Y_n;\, Y_n \ge 2] \cdot\mathrm E[Y_{n} \mid Y_n \ge 1]. \tag{A}\end{align}
This regularity assumption is notably mild. As we shall explain in the next section, it is fulfilled for distributions  $f_n$,
$f_n$,  $n \ge 1$, belonging to any common class of probability measures, like Poisson, binomial, hypergeometric, geometric, linear fractional or negative binomial distributions, without any restriction on the parameters. It is also satisfied in the case that the random variables
$n \ge 1$, belonging to any common class of probability measures, like Poisson, binomial, hypergeometric, geometric, linear fractional or negative binomial distributions, without any restriction on the parameters. It is also satisfied in the case that the random variables  $Y_n$,
$Y_n$,  $n \ge 1$, are a.s. uniformly bounded by a constant
$n \ge 1$, are a.s. uniformly bounded by a constant  $c \lt \infty$. To see this, take into account that we have
$c \lt \infty$. To see this, take into account that we have  $\mathrm E[Y_{n} \mid Y_n \ge 1] \ge 1$. Since direct verification of (A) may be tedious in examples, we shall present in the next section a third moment condition which implies (A) and which can often be easily checked.
$\mathrm E[Y_{n} \mid Y_n \ge 1] \ge 1$. Since direct verification of (A) may be tedious in examples, we shall present in the next section a third moment condition which implies (A) and which can often be easily checked.
Let us call a BPVE regular if it fulfils condition (A).
Remark 1. (A property of consistency) Observe that together with a BPVE  $(Z_n)_{n \ge 0}$, any subsequence
$(Z_n)_{n \ge 0}$, any subsequence  $(Z_{n_i})_{i \ge 0}$ with
$(Z_{n_i})_{i \ge 0}$ with  $n_0\,:\!=0 \lt n_1 \lt n_2 <\ldots$ is a BPVE, too. We note that the condition (A) is then transmitted, i.e. any subsequence of a regular BPVE is regular, too. The proof will be given after Lemma 6 below.
$n_0\,:\!=0 \lt n_1 \lt n_2 <\ldots$ is a BPVE, too. We note that the condition (A) is then transmitted, i.e. any subsequence of a regular BPVE is regular, too. The proof will be given after Lemma 6 below.
Before presenting our results, let us agree on the following notational conventions. Let  $\mathcal P$ be the set of all probability measures on
$\mathcal P$ be the set of all probability measures on  $\mathbb N_0$. The weights of
$\mathbb N_0$. The weights of  $f\in \mathcal P$ are named f[k],
$f\in \mathcal P$ are named f[k],  $k \in \mathbb N_0$. We set
$k \in \mathbb N_0$. We set
 \[ f(s)\,:\!= \sum_{k=0}^\infty s^k f[k], \qquad 0 \le s \le 1 . \]
\[ f(s)\,:\!= \sum_{k=0}^\infty s^k f[k], \qquad 0 \le s \le 1 . \]
Thus, we denote the probability measure f and its generating function by one and the same symbol. This facilitates presentation and will cause no confusion. Keep in mind that each operation applied to these measures has to be understood as an operation applied to their generating functions. Thus,  $f_1f_2$ stands not only for the multiplication of the generating functions
$f_1f_2$ stands not only for the multiplication of the generating functions  $f_1,f_2$ but also for the convolution of the respective measures. Also,
$f_1,f_2$ but also for the convolution of the respective measures. Also,  $f_1 \circ f_2$ expresses the composition of generating functions as well as the resulting probability measure. We shall consider the mean and second factorial moment of a random variable Y with distribution f,
$f_1 \circ f_2$ expresses the composition of generating functions as well as the resulting probability measure. We shall consider the mean and second factorial moment of a random variable Y with distribution f,
 \[ \mathrm E[Y]= f^{\prime}(1), \quad \mathrm E[Y(Y-1)] = f^{\prime\prime}(1),\]
\[ \mathrm E[Y]= f^{\prime}(1), \quad \mathrm E[Y(Y-1)] = f^{\prime\prime}(1),\]and its normalized second factorial moment and normalized variance
 \[ \nu\,:\!= \frac{\mathrm E[Y(Y-1)]}{\mathrm E[Y]^2}= \frac{f^{\prime\prime}(1)}{f^{\prime}(1)^2}, \quad \rho\,:\!= \frac{\mathrm{Var}[Y]}{\mathrm E[Y]^2}=\nu+ \frac 1{\mathrm E[Y]} -1 .\]
\[ \nu\,:\!= \frac{\mathrm E[Y(Y-1)]}{\mathrm E[Y]^2}= \frac{f^{\prime\prime}(1)}{f^{\prime}(1)^2}, \quad \rho\,:\!= \frac{\mathrm{Var}[Y]}{\mathrm E[Y]^2}=\nu+ \frac 1{\mathrm E[Y]} -1 .\] We shall discuss branching processes in a varying environment along the lines of ordinary Galton–Watson processes. For  $n \ge 1$, let
$n \ge 1$, let
 \[ q\,:\!= \mathrm P(Z_\infty =0), \quad \mu_n\,:\!= f^{\prime}_{1}(1) \cdots f^{\prime}_{n}(1), \quad \nu_n\,:\!= \frac{f^{\prime\prime}_{n}(1)}{f^{\prime}_{n}(1)^2} , \quad \rho_n\,:\!= \nu_n+ \frac 1{f^{\prime}_{n}(1)}-1 , \]
\[ q\,:\!= \mathrm P(Z_\infty =0), \quad \mu_n\,:\!= f^{\prime}_{1}(1) \cdots f^{\prime}_{n}(1), \quad \nu_n\,:\!= \frac{f^{\prime\prime}_{n}(1)}{f^{\prime}_{n}(1)^2} , \quad \rho_n\,:\!= \nu_n+ \frac 1{f^{\prime}_{n}(1)}-1 , \]
and also  $\mu_0\,:\!=1$. Thus, q is the probability of extinction and
$\mu_0\,:\!=1$. Thus, q is the probability of extinction and  $\mu_n= \mathrm E[Z_n]$,
$\mu_n= \mathrm E[Z_n]$,  $n \ge 0$. Note that for the standardized factorial moments
$n \ge 0$. Note that for the standardized factorial moments  $ \nu_n$ we have
$ \nu_n$ we have  $ \nu_n \lt \infty$ under Assumption (A). This implies
$ \nu_n \lt \infty$ under Assumption (A). This implies  $\mathrm E[Z_n^2] \lt \infty$ for all
$\mathrm E[Z_n^2] \lt \infty$ for all  $n \ge 0$ (see Lemma 4 below).
$n \ge 0$ (see Lemma 4 below).
Assumption (A) is a mild requirement with substantial consequences, as seen from the following diverse necessary and sufficient criteria for almost sure extinction.
Theorem 1. Assume (A). Then the conditions
(i)
 $q=1$,
$q=1$,(ii)
 $\mathrm E[Z_n]^2 = o(\mathrm E[Z_n^2])$ as
$\mathrm E[Z_n]^2 = o(\mathrm E[Z_n^2])$ as  $n \to \infty$,
$n \to \infty$,(iii)
 $ \sum\limits_{k=1}^\infty \frac {\rho_k}{\mu_{k-1}}= \infty$,
$ \sum\limits_{k=1}^\infty \frac {\rho_k}{\mu_{k-1}}= \infty$,(iv)
 $ \sum\limits_{k=1}^\infty \frac {\nu_k}{\mu_{k-1}}= \infty$ or
$ \sum\limits_{k=1}^\infty \frac {\nu_k}{\mu_{k-1}}= \infty$ or  $ \mu_n \to 0$
$ \mu_n \to 0$
are equivalent. Moreover, the conditions
(v)
 $q<1$,
$q<1$,(vi)
 $\mathrm E[Z_n^2] = O(\mathrm E[Z_n]^2)$ as
$\mathrm E[Z_n^2] = O(\mathrm E[Z_n]^2)$ as  $n \to \infty$,
$n \to \infty$,(vii)
 $ \sum\limits_{k=1}^\infty \frac {\rho_k}{\mu_{k-1}} \lt \infty$,
$ \sum\limits_{k=1}^\infty \frac {\rho_k}{\mu_{k-1}} \lt \infty$,(viii)
 $ \sum\limits_{k=1}^\infty \frac {\nu_k}{\mu_{k-1}} \lt \infty$and there exists
$ \sum\limits_{k=1}^\infty \frac {\nu_k}{\mu_{k-1}} \lt \infty$and there exists  $0 \lt r\le \infty$such that
$0 \lt r\le \infty$such that  $\mu_n \to r$
$\mu_n \to r$
are equivalent.
These conditions are useful in different ways. Condition (iii)/(vii) appears to be a particulary suitable criterion for almost sure extinction, whereas conditions (iv) and (viii) will prove helpful for the classification of BPVEs. Condition (vi) will allow us to determine the growth rate of  $Z_{n}$ (see Theorem 2). Observe that (ii) can be rewritten as
$Z_{n}$ (see Theorem 2). Observe that (ii) can be rewritten as  $\mathrm E[Z_n]=o(\sqrt{\mathrm{Var}[Z_n]})$. Briefly speaking, this means that under (A) we have almost sure extinction if and only if the noise dominates the average growth in the long run.
$\mathrm E[Z_n]=o(\sqrt{\mathrm{Var}[Z_n]})$. Briefly speaking, this means that under (A) we have almost sure extinction if and only if the noise dominates the average growth in the long run.
We point out that conditions (iii), (iv), (vii) and (viii) access not only the expectations  $\mu_n$ but also the second moments. This is a novel aspect in comparsion to ordinary Galton–Watson processes and also to Agresti’s classical criterion on BPVEs [Reference Agresti1, Theorem 2]. Agresti’s result provides almost sure extinction if and only if
$\mu_n$ but also the second moments. This is a novel aspect in comparsion to ordinary Galton–Watson processes and also to Agresti’s classical criterion on BPVEs [Reference Agresti1, Theorem 2]. Agresti’s result provides almost sure extinction if and only if  $\sum_{k\ge1} 1/\mu_{k-1} = \infty$. He could do so by virtue of his stronger assumptions, which exclude, e.g., asymptotically degenerate processes. In our setting there is the possibility that we have both
$\sum_{k\ge1} 1/\mu_{k-1} = \infty$. He could do so by virtue of his stronger assumptions, which exclude, e.g., asymptotically degenerate processes. In our setting there is the possibility that we have both  $\sum_{k \ge 1} \rho_k/\mu_{k-1}=\infty$ and
$\sum_{k \ge 1} \rho_k/\mu_{k-1}=\infty$ and  $\sum_{k \ge 1} 1/\mu_{k-1}<\infty$, and also the other way round. This is shown by the following examples.
$\sum_{k \ge 1} 1/\mu_{k-1}<\infty$, and also the other way round. This is shown by the following examples.
Example 1. Let  $Y_n$ take just the values
$Y_n$ take just the values  $n+2$ and 0, with
$n+2$ and 0, with  $\mathrm P(Y_n= n+2)= n^{-1}$. Then
$\mathrm P(Y_n= n+2)= n^{-1}$. Then  $\mathrm E[Y_n(Y_n-1)]\sim n$,
$\mathrm E[Y_n(Y_n-1)]\sim n$,  $\mathrm E[Y_n]= 1+ 2/n$,
$\mathrm E[Y_n]= 1+ 2/n$,  $\mathrm E[Y_n-1 \mid Y_n\ge 1]\sim n$, and thus (A) is fulfilled. Also,
$\mathrm E[Y_n-1 \mid Y_n\ge 1]\sim n$, and thus (A) is fulfilled. Also,  $\mu_n \sim n^2/2$ and
$\mu_n \sim n^2/2$ and  $\rho_n\sim n$, hence
$\rho_n\sim n$, hence  $\sum_{k \ge 1} 1/\mu_{k-1}<\infty$ and
$\sum_{k \ge 1} 1/\mu_{k-1}<\infty$ and  $\sum_{k \ge 1} \rho_k/\mu_{k-1}=\infty$.
$\sum_{k \ge 1} \rho_k/\mu_{k-1}=\infty$.
Example 2. Let  $Y_n$ take just the values 0, 1 and 2, with
$Y_n$ take just the values 0, 1 and 2, with  $\mathrm P(Y_n=0)=\mathrm P(Y_n=2) = 1/(2n^2)$. Then
$\mathrm P(Y_n=0)=\mathrm P(Y_n=2) = 1/(2n^2)$. Then  $\mathrm E[Y_n(Y_n-1)] \sim n^{-2}$,
$\mathrm E[Y_n(Y_n-1)] \sim n^{-2}$,  $\mathrm E[Y_n]=1$ and
$\mathrm E[Y_n]=1$ and  $\mathrm E[Y_n-1\mid Y_n \ge 1]\sim 1/(2n^2)$, and thus (A) is fulfilled. Also,
$\mathrm E[Y_n-1\mid Y_n \ge 1]\sim 1/(2n^2)$, and thus (A) is fulfilled. Also,  $\mu_n=1$ and
$\mu_n=1$ and  $\rho_n \sim n^{-2}$, hence
$\rho_n \sim n^{-2}$, hence  $\sum_{k \ge 1} 1/\mu_{k-1}=\infty$ and
$\sum_{k \ge 1} 1/\mu_{k-1}=\infty$ and  $\sum_{k \ge 1} \rho_k/\mu_{k-1}<\infty$.
$\sum_{k \ge 1} \rho_k/\mu_{k-1}<\infty$.
The last example exhibits an asymptotically degenerate branching process, as seen from Corollary 1 below.
Next we turn to the normalized population sizes
 \[ W_n \,:\!= \frac {Z_n}{\mu_n}, \qquad n \ge 0\ . \]
\[ W_n \,:\!= \frac {Z_n}{\mu_n}, \qquad n \ge 0\ . \]
Clearly,  $(W_n)_{n \ge 0}$ constitutes a non-negative martingale, and thus there exists an integrable random variable
$(W_n)_{n \ge 0}$ constitutes a non-negative martingale, and thus there exists an integrable random variable  $W\ge 0$ such that we have
$W\ge 0$ such that we have  $W_n \to W$ a.s. as
$W_n \to W$ a.s. as  $n\to \infty$. With (A), the random variable W exhibits the dichotomy known for Galton–Watson processes.
$n\to \infty$. With (A), the random variable W exhibits the dichotomy known for Galton–Watson processes.
Theorem 2. For a regular BPVE we have:
(i) If
 $q=1$then
$q=1$then  $W=0$a.s.
$W=0$a.s.(ii) If
 $q\lt1$then
$q\lt1$then  $\mathrm E[W]=1$,
$\mathrm E[W]=1$,  $\mathrm E[W^2]<\infty$and
$\mathrm E[W^2]<\infty$and  $\mathrm P(W=0)=q$.
$\mathrm P(W=0)=q$.
In particular, in the case of  $q<1$ the martingale
$q<1$ the martingale  $(W_n)_{n\ge 0}$ is convergent in
$(W_n)_{n\ge 0}$ is convergent in  $\mathcal L^2$, implying
$\mathcal L^2$, implying
 \begin{align}\mathrm{V}\text{ar}[W] = \sum_{k=1}^\infty \frac {\rho_k}{\mu_{k-1}}.\end{align}
\begin{align}\mathrm{V}\text{ar}[W] = \sum_{k=1}^\infty \frac {\rho_k}{\mu_{k-1}}.\end{align}
This formula goes back to Fearn [Reference Fearn10]. We point out that Assumption (A) excludes the possibility of  $\mathrm P(W=0) \gt q$ and, in particular, of different rates of growth as in the examples constructed by MacPhee and Schuh [Reference MacPhee and Schuh19] (see also [Reference D’Souza6, Reference D’Souza and Biggins7]). By means of Theorem 2(ii) we also gain further insight into asymptotically degenerate processes. Under Assumption (A) they are just those processes which fulfil the properties
$\mathrm P(W=0) \gt q$ and, in particular, of different rates of growth as in the examples constructed by MacPhee and Schuh [Reference MacPhee and Schuh19] (see also [Reference D’Souza6, Reference D’Souza and Biggins7]). By means of Theorem 2(ii) we also gain further insight into asymptotically degenerate processes. Under Assumption (A) they are just those processes which fulfil the properties  $q<1$ and
$q<1$ and  $0 \lt \lim_{n\to \infty} \mu_n \lt \infty$. Also, taking Theorem 1(v) and (viii) into account we obtain the following corollary.
$0 \lt \lim_{n\to \infty} \mu_n \lt \infty$. Also, taking Theorem 1(v) and (viii) into account we obtain the following corollary.
Corollary 1. A regular BPVE is asymptotically degenerate if and only if both  $\sum_{k=1}^\infty \nu_k \lt \infty$and the sequence
$\sum_{k=1}^\infty \nu_k \lt \infty$and the sequence  $(\mu_n)_{n \ge 0}$has a positive, finite limit. Then
$(\mu_n)_{n \ge 0}$has a positive, finite limit. Then  $Z_\infty \lt \infty$a.s.
$Z_\infty \lt \infty$a.s.
Now we address the behaviour of the random variables  $Z_n$ conditioned on the events that
$Z_n$ conditioned on the events that  $Z_n>0$. The next theorem shows that their values largely follow the corresponding conditional expectations
$Z_n>0$. The next theorem shows that their values largely follow the corresponding conditional expectations  $\mathrm E[Z_n \mid Z_n \gt 0]$. For
$\mathrm E[Z_n \mid Z_n \gt 0]$. For  $n \ge 0$ let
$n \ge 0$ let
 \[a_n \,:\!= 1+ \mu_n \sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}} . \]
\[a_n \,:\!= 1+ \mu_n \sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}} . \]Theorem 3. For a regular BPVE, the sequence of random variables  $Z_n/a_n$conditioned on
$Z_n/a_n$conditioned on  $Z_n \gt 0$,
$Z_n \gt 0$,  $n \ge 0$, is tight, i.e. for any
$n \ge 0$, is tight, i.e. for any  $\varepsilon \gt 0$there is a
$\varepsilon \gt 0$there is a  $u<\infty$such that, for all
$u<\infty$such that, for all  $n \ge 0$,
$n \ge 0$,
 \begin{align} \mathrm P\bigg( \frac{Z_n}{a_n} \gt u \mid Z_n \gt 0\bigg) \le \varepsilon ;\end{align}
\begin{align} \mathrm P\bigg( \frac{Z_n}{a_n} \gt u \mid Z_n \gt 0\bigg) \le \varepsilon ;\end{align}moreover, there exist numbers  $\theta \gt 0$and
$\theta \gt 0$and  $u \gt 0$such that, for all
$u \gt 0$such that, for all  $n\ge 0$,
$n\ge 0$,
 \begin{align} \mathrm P\bigg( \frac{Z_n}{a_n} \gt u \mid Z_n \gt 0\bigg) \ge \theta .\end{align}
\begin{align} \mathrm P\bigg( \frac{Z_n}{a_n} \gt u \mid Z_n \gt 0\bigg) \ge \theta .\end{align}Also, we have
 \begin{align} \gamma a_n \le \mathrm E[Z_n \mid Z_n \gt 0] \le a_n\end{align}
\begin{align} \gamma a_n \le \mathrm E[Z_n \mid Z_n \gt 0] \le a_n\end{align}with some constant  $\gamma \gt 0$, so that we may replace
$\gamma \gt 0$, so that we may replace  $a_n$ by
$a_n$ by  $\mathrm E[Z_n\mid Z_n>0]$in (2) and in (3).
$\mathrm E[Z_n\mid Z_n>0]$in (2) and in (3).
For  $q<1$ we do not learn anything new from this theorem; here, Theorem 2(ii) gives much preciser information. Thus, let us focus on the case
$q<1$ we do not learn anything new from this theorem; here, Theorem 2(ii) gives much preciser information. Thus, let us focus on the case  $q=1$, the situation of almost sure extinction. At first sight one might expect that the constant
$q=1$, the situation of almost sure extinction. At first sight one might expect that the constant  $\theta$ in (3) can be chosen arbitrarily close to 1, if only u gets sufficiently small. This will apply to many interesting cases, but it is not always true. The following example gives an illustration.
$\theta$ in (3) can be chosen arbitrarily close to 1, if only u gets sufficiently small. This will apply to many interesting cases, but it is not always true. The following example gives an illustration.
Example 3. For  $n \ge 1$ let
$n \ge 1$ let
 \[ f_{2n-1}[1]= 2^{-n} , \quad f_{2n-1}[0] =1-2^{-n} \quad \text{and} \quad f_{2n}[2^{n+1}-1]=f_{2n}[1] = \frac 12 . \]
\[ f_{2n-1}[1]= 2^{-n} , \quad f_{2n-1}[0] =1-2^{-n} \quad \text{and} \quad f_{2n}[2^{n+1}-1]=f_{2n}[1] = \frac 12 . \]
It is easy to check that (A) is valid (as well as the conditions (B) and (C) below). We have  $f^{\prime}_{2n-1}(1)= 2^{-n}$ and
$f^{\prime}_{2n-1}(1)= 2^{-n}$ and  $f^{\prime}_{2n}(1)= 2^{n}$, hence
$f^{\prime}_{2n}(1)= 2^{n}$, hence
 \[ \mu_{2n-1}= 2^{-n} \quad \text{and} \quad \mu_{2n}= 1 \]
\[ \mu_{2n-1}= 2^{-n} \quad \text{and} \quad \mu_{2n}= 1 \]
for all  $n \ge 1$. In particular, we have
$n \ge 1$. In particular, we have  $Z_{2n-1}\to 0$ in probability, which entails
$Z_{2n-1}\to 0$ in probability, which entails  $q=1$. Also,
$q=1$. Also,  $\nu_{2n-1}=0$ and
$\nu_{2n-1}=0$ and  $\nu_{2n} \sim 2$ as
$\nu_{2n} \sim 2$ as  $n \to \infty$, implying
$n \to \infty$, implying
 \[\sum_{k=1}^{2n} \frac{\nu_k}{\mu_{k-1}} \sim \sum_{k=1}^n 2^{k+1} \sim 2^{n+2} \quad \text{and} \quad \sum_{k=1}^{2n-1} \frac{\nu_k}{\mu_{k-1}}= \sum_{k=1}^{2n-2} \frac{\nu_k}{\mu_{k-1}}\sim 2^{n+1} , \]
\[\sum_{k=1}^{2n} \frac{\nu_k}{\mu_{k-1}} \sim \sum_{k=1}^n 2^{k+1} \sim 2^{n+2} \quad \text{and} \quad \sum_{k=1}^{2n-1} \frac{\nu_k}{\mu_{k-1}}= \sum_{k=1}^{2n-2} \frac{\nu_k}{\mu_{k-1}}\sim 2^{n+1} , \]and
 \[ a_{2n-1} \sim 3 \quad \text{and}\quad a_{2n} \sim 2^{n+2}. \]
\[ a_{2n-1} \sim 3 \quad \text{and}\quad a_{2n} \sim 2^{n+2}. \]
From Theorem 3 it follows that there is a  $z \lt \infty$ such that
$z \lt \infty$ such that
 \[ \mathrm P(Z_{2n-1} \gt z \mid Z_{2n-1} \gt 0) \le \frac 12 \]
\[ \mathrm P(Z_{2n-1} \gt z \mid Z_{2n-1} \gt 0) \le \frac 12 \]
for all  $n \ge 1$. Therefore,
$n \ge 1$. Therefore,
 \begin{align*}\mathrm P( Z_{2n} \le z \mid Z_{2n}>0) &= \mathrm P(Z_{2n}\le z \mid Z_{2n-1}>0) \notag \\&\ge \mathrm P(Z_{2n-1}\le z \mid Z_{2n-1} \gt 0) f_{2n}[1]^z \notag \\&\ge 2^{-z-1}\end{align*}
\begin{align*}\mathrm P( Z_{2n} \le z \mid Z_{2n}>0) &= \mathrm P(Z_{2n}\le z \mid Z_{2n-1}>0) \notag \\&\ge \mathrm P(Z_{2n-1}\le z \mid Z_{2n-1} \gt 0) f_{2n}[1]^z \notag \\&\ge 2^{-z-1}\end{align*}
for all  $n \ge 1$, and for any
$n \ge 1$, and for any  $u>0$,
$u>0$,
 \begin{align}\mathrm P( Z_{2n}/a_{2n} \gt u \mid Z_{2n} \gt 0) \le 1 - 2^{-z-1}\end{align}
\begin{align}\mathrm P( Z_{2n}/a_{2n} \gt u \mid Z_{2n} \gt 0) \le 1 - 2^{-z-1}\end{align}
if  $a_{2n} \ge z/u$. Since
$a_{2n} \ge z/u$. Since  $a_{2n} \to \infty$, the constant
$a_{2n} \to \infty$, the constant  $\theta$ from (3) cannot take a value above
$\theta$ from (3) cannot take a value above  $1 - 2^{-z-1}$ in this example.
$1 - 2^{-z-1}$ in this example.
This example suggests that quite different scenarios may occur for BPVEs with  $q=1$, and that their behaviour may abruptly change from one subsequence to the next. We point out that Assumption (A) does not put (e.g. for Poisson distributions) any restrictions on the expectation
$q=1$, and that their behaviour may abruptly change from one subsequence to the next. We point out that Assumption (A) does not put (e.g. for Poisson distributions) any restrictions on the expectation  $\mu_n$,
$\mu_n$,  $n \ge 1$, allowing a variety of examples. Of special interest is the case that the numbers
$n \ge 1$, allowing a variety of examples. Of special interest is the case that the numbers  $a_n$ are uniformly bounded. Here, Theorem 3 reads as follows.
$a_n$ are uniformly bounded. Here, Theorem 3 reads as follows.
Corollary 2. Under Assumption (A) the conditions
(i) the sequence of random variables
 $Z_n$conditioned on the events that
$Z_n$conditioned on the events that  $Z_n \gt 0$,
$Z_n \gt 0$,  $n \ge 0$, is tight,
$n \ge 0$, is tight,(ii)
 $\sup_{n\ge 0} \mathrm E[Z_n \mid Z_n \gt 0] \lt \infty$,
$\sup_{n\ge 0} \mathrm E[Z_n \mid Z_n \gt 0] \lt \infty$,(iii)
 $ \sum\limits_{k=1}^n \frac{\nu_k}{\mu_{k-1}} = O \Big( \frac 1{\mu_n}\Big)$as
$ \sum\limits_{k=1}^n \frac{\nu_k}{\mu_{k-1}} = O \Big( \frac 1{\mu_n}\Big)$as  $n \to \infty$,
$n \to \infty$,
are equivalent.
For an ordinary Galton–Watson process these three conditions apply just in the subcritical regime, and then the conditioned random variables  $Z_n$ have a limiting distribution. It is easy to see that such a feature will not hold in general for a BPVE. Indeed, there are two offspring distributions
$Z_n$ have a limiting distribution. It is easy to see that such a feature will not hold in general for a BPVE. Indeed, there are two offspring distributions  $\skew2\hat{f}$ and
$\skew2\hat{f}$ and  $\skew2\tilde{f}$ such that the limiting distributions
$\skew2\tilde{f}$ such that the limiting distributions  $\skew2\hat{g}$ and
$\skew2\hat{g}$ and  $\skew2\tilde{g}$ for the corresponding conditional Galton–Watson processes differ from each other. Choose an increasing sequence
$\skew2\tilde{g}$ for the corresponding conditional Galton–Watson processes differ from each other. Choose an increasing sequence  $0=n_0 \lt n_1 <n_2 \lt \cdots$ of natural numbers and consider the BPVE
$0=n_0 \lt n_1 <n_2 \lt \cdots$ of natural numbers and consider the BPVE  $(Z_n)_{n \ge 0}$ in the varying environment
$(Z_n)_{n \ge 0}$ in the varying environment  $v=(\,f_1,f_2, \ldots\!)$, where
$v=(\,f_1,f_2, \ldots\!)$, where  $f_n= \skew2\hat{f}$ for
$f_n= \skew2\hat{f}$ for  $n_{2k} \lt n \le n_{2k+1}$,
$n_{2k} \lt n \le n_{2k+1}$,  $k \in \mathbb N_0$, and
$k \in \mathbb N_0$, and  $f_n = \skew2\tilde{f}$ otherwise. Then it is obvious that
$f_n = \skew2\tilde{f}$ otherwise. Then it is obvious that  $Z_{n_{2k+1}}$ given the event
$Z_{n_{2k+1}}$ given the event  $Z_{n_{2k+1}}>0$ converges in distribution to
$Z_{n_{2k+1}}>0$ converges in distribution to  $\skew2\hat{g}$, and
$\skew2\hat{g}$, and  $Z_{n_{2k}}$ given the event
$Z_{n_{2k}}$ given the event  $Z_{n_{2k}}>0$ converges in distribution to
$Z_{n_{2k}}>0$ converges in distribution to  $\skew2\tilde{g}$, provided that the sequence
$\skew2\tilde{g}$, provided that the sequence  $(n_k)_{k \ge 0}$ is increasing sufficiently fast.
$(n_k)_{k \ge 0}$ is increasing sufficiently fast.
Thus, it may come as a surprise that in the opposite situation,  $\mu_{n}^{-1}=o(\sum_{k=1}^{n} \frac{\nu_k}{\mu_{k-1}})$, we encounter a distinctive behaviour of the conditional-limit distributions of
$\mu_{n}^{-1}=o(\sum_{k=1}^{n} \frac{\nu_k}{\mu_{k-1}})$, we encounter a distinctive behaviour of the conditional-limit distributions of  $Z_n$, which is in accordance with Yaglom’s theorem for ordinary Galton–Watson processes. For technical reasons we have to somewhat strengthen Assumption (A). We require that for every
$Z_n$, which is in accordance with Yaglom’s theorem for ordinary Galton–Watson processes. For technical reasons we have to somewhat strengthen Assumption (A). We require that for every  $\varepsilon \gt 0$ there is a constant
$\varepsilon \gt 0$ there is a constant  $c_\varepsilon \lt \infty$ such that, for all natural numbers
$c_\varepsilon \lt \infty$ such that, for all natural numbers  $n \ge 1$,
$n \ge 1$,
 \begin{align}\mathrm E[ Y_n^2 ;\, Y_n \gt c_\varepsilon(1+ \mathrm E[Y_n])] \le \varepsilon \mathrm E [ Y_n^2;\, Y_n \ge 2] .\tag{B}\end{align}
\begin{align}\mathrm E[ Y_n^2 ;\, Y_n \gt c_\varepsilon(1+ \mathrm E[Y_n])] \le \varepsilon \mathrm E [ Y_n^2;\, Y_n \ge 2] .\tag{B}\end{align}
This condition is again widely satisfied, as we shall explain in the next section. It implies Assumption (A). Namely, for  $\varepsilon=1/2$ we have
$\varepsilon=1/2$ we have
 \begin{align}\mathrm E[Y_n^2;\, Y_n \ge 2] &\le 2 \mathrm E[ Y_n^2 ;\, 2 \le Y_n \le c_{1/2}(1+ \mathrm E[Y_n])]\notag \\& \le 2c_{1/2} (1+ \mathrm E[Y_n]) \mathrm E[Y_n;\, Y_n \ge 2] .\end{align}
\begin{align}\mathrm E[Y_n^2;\, Y_n \ge 2] &\le 2 \mathrm E[ Y_n^2 ;\, 2 \le Y_n \le c_{1/2}(1+ \mathrm E[Y_n])]\notag \\& \le 2c_{1/2} (1+ \mathrm E[Y_n]) \mathrm E[Y_n;\, Y_n \ge 2] .\end{align}
Since  $1+ \mathrm E[Y_n] \le 2\mathrm E[Y_n \mid Y_n \ge 1]$, we obtain (A) with
$1+ \mathrm E[Y_n] \le 2\mathrm E[Y_n \mid Y_n \ge 1]$, we obtain (A) with  $c=4c_{1/2}$.
$c=4c_{1/2}$.
Theorem 4. Let (B) be satisfied and let  $q=1$. Then the following conditions are equivalent:
$q=1$. Then the following conditions are equivalent:
(i) There is a sequence
 $b_n$,
$b_n$,  $n \ge 0$, of positive numbers such that
$n \ge 0$, of positive numbers such that  $Z_n/b_n$conditioned on the event
$Z_n/b_n$conditioned on the event  $Z_n>0$converges in distribution to a standard exponential distribution as
$Z_n>0$converges in distribution to a standard exponential distribution as  $n \to \infty$;
$n \to \infty$;(ii)
 $\mathrm E[Z_n \mid Z_n \gt 0] \to \infty$as
$\mathrm E[Z_n \mid Z_n \gt 0] \to \infty$as  $n \to \infty$;
$n \to \infty$;(iii)
 $\frac1{\mu_n} = o \bigg( \sum\limits_{k=1}^n \frac {\nu_k}{\mu_{k-1}} \bigg)$as
$\frac1{\mu_n} = o \bigg( \sum\limits_{k=1}^n \frac {\nu_k}{\mu_{k-1}} \bigg)$as  $n \to \infty$.
$n \to \infty$.
Under these conditions we may set  $b_n\,:\!= \mathrm E[Z_n \mid Z_n \gt 0]$, and we have
$b_n\,:\!= \mathrm E[Z_n \mid Z_n \gt 0]$, and we have
 \[ \mathrm E[Z_n \mid Z_n \gt 0] \sim \frac{\mu_n }2\sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}},\]
\[ \mathrm E[Z_n \mid Z_n \gt 0] \sim \frac{\mu_n }2\sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}},\]or equivalently
 \[ \mathrm P(Z_n \gt 0) \sim 2\bigg(\sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}}\bigg)^{-1}\]
\[ \mathrm P(Z_n \gt 0) \sim 2\bigg(\sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}}\bigg)^{-1}\]as  $n \to \infty$.
$n \to \infty$.
This theorem covers the classical results of Kolmogorov and Yaglom for critical Galton–Watson processes in the finite variance case (without further moment restrictions), since then (B) is trivially satisfied.
Our results show how to implement a classification of regular BPVEs which connects to the notions used for classical Galton–Watson processes. If  $q<1$, then in view of Theorem 2 and Corollary 1 we distinguish two regimes. There is the supercritical regime in the case of
$q<1$, then in view of Theorem 2 and Corollary 1 we distinguish two regimes. There is the supercritical regime in the case of  $\mathrm E[Z_n]\to \infty$, and the asymptotically degenerate regime otherwise. If, on the other hand, we have
$\mathrm E[Z_n]\to \infty$, and the asymptotically degenerate regime otherwise. If, on the other hand, we have  $q=1$, then Theorem 4 suggests characterizing the critical regime by the condition
$q=1$, then Theorem 4 suggests characterizing the critical regime by the condition  ${\mathrm E[Z_n \mid Z_n>0]\to \infty}$ (and not just by some condition on the limiting behaviour of
${\mathrm E[Z_n \mid Z_n>0]\to \infty}$ (and not just by some condition on the limiting behaviour of  $\mu_n$, as one might do in a first attempt), and to allocate the other BPVEs to the subcritical regime. In this way we differentiate the clear-cut limiting property of critical BPVEs from the indeterminacy of the remaining processes. In this classification a subcritical BPVE
$\mu_n$, as one might do in a first attempt), and to allocate the other BPVEs to the subcritical regime. In this way we differentiate the clear-cut limiting property of critical BPVEs from the indeterminacy of the remaining processes. In this classification a subcritical BPVE  $(Z_n)_{n\ge 0}$ exhibits subcritical behaviour in the sense that according to Theorem 3 the random variables
$(Z_n)_{n\ge 0}$ exhibits subcritical behaviour in the sense that according to Theorem 3 the random variables  $Z_n$ conditioned on
$Z_n$ conditioned on  $Z_n>0$ are tight, at least along some subsequence in which the
$Z_n>0$ are tight, at least along some subsequence in which the  $a_n$ stay bounded. The
$a_n$ stay bounded. The  $Z_n$ may diverge with positive probability along some other subsequence, yet this does not in general imply critical behaviour in the sense that along that subsequence the random variables
$Z_n$ may diverge with positive probability along some other subsequence, yet this does not in general imply critical behaviour in the sense that along that subsequence the random variables  $Z_{n}$, conditioned on
$Z_{n}$, conditioned on  $Z_{n}>0$ and suitably scaled, have asymptotically an exponential distribution. For a counterexample we refer to Example 3 and (5).
$Z_{n}>0$ and suitably scaled, have asymptotically an exponential distribution. For a counterexample we refer to Example 3 and (5).
By means of Theorems 1 and 3 we may streamline the determining conditions of the four regimes, as summarized in the subsequent overview.
Proposition 1. A regular BPVE is
 \begin{align*}\textit{{ supercritical} if and only if} & \ \lim_{n\to \infty} \mu_n=\infty\ \textit{and} \ \sum_{k=1}^\infty \frac{\nu_k}{\mu_{k-1}} \lt \infty ,\\\textit{{ asymptotically degenerate} if and only if} & \ 0 \lt \lim_{n\to \infty} \mu_n<\infty \ \textit{and}\ \sum_{k=1}^\infty \frac{\nu_k}{\mu_{k-1}} \lt \infty ,\\\textit{{ critical} if and only if} & \ \lim_{n \to \infty} \mu_n \sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}} =\infty \ \textit{and}\ \sum_{k=1}^\infty \frac{\nu_k}{\mu_{k-1}} = \infty,\\\textit{{ subcritical} if and only if} & \ \liminf_{n \to \infty}\mu_n=0 \ \textit{and}\ \liminf_{n\to \infty}\mu_n\sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}} <\infty .\end{align*}
\begin{align*}\textit{{ supercritical} if and only if} & \ \lim_{n\to \infty} \mu_n=\infty\ \textit{and} \ \sum_{k=1}^\infty \frac{\nu_k}{\mu_{k-1}} \lt \infty ,\\\textit{{ asymptotically degenerate} if and only if} & \ 0 \lt \lim_{n\to \infty} \mu_n<\infty \ \textit{and}\ \sum_{k=1}^\infty \frac{\nu_k}{\mu_{k-1}} \lt \infty ,\\\textit{{ critical} if and only if} & \ \lim_{n \to \infty} \mu_n \sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}} =\infty \ \textit{and}\ \sum_{k=1}^\infty \frac{\nu_k}{\mu_{k-1}} = \infty,\\\textit{{ subcritical} if and only if} & \ \liminf_{n \to \infty}\mu_n=0 \ \textit{and}\ \liminf_{n\to \infty}\mu_n\sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}} <\infty .\end{align*}
Note that convergence of the means  $\mu_n$ is not enforced in the critical case; they may diverge, converge to zero or even oscillate in between.
$\mu_n$ is not enforced in the critical case; they may diverge, converge to zero or even oscillate in between.
Example 4. In the case  $0 \lt \inf_n \nu_n \le \sup_n \nu_n \lt \infty$ (as e.g. for Poisson variables) the classification simplifies. Here, we are in the supercritical regime if and only if
$0 \lt \inf_n \nu_n \le \sup_n \nu_n \lt \infty$ (as e.g. for Poisson variables) the classification simplifies. Here, we are in the supercritical regime if and only if  $\sum_{k \ge 0} 1/\mu_k \lt \infty$ (enforcing
$\sum_{k \ge 0} 1/\mu_k \lt \infty$ (enforcing  $\mu_n \to \infty$). Asymptotically degenerate behaviour is excluded, and there is plenty of room for critical processes, i.e. for processes which conform to the conditions
$\mu_n \to \infty$). Asymptotically degenerate behaviour is excluded, and there is plenty of room for critical processes, i.e. for processes which conform to the conditions  $\sum_{k \ge 0} 1/\mu_k = \infty$ and
$\sum_{k \ge 0} 1/\mu_k = \infty$ and  $1/\mu_n =o(\sum_{k=0}^{n-1} 1/\mu_k)$. The second requirement is e.g. fulfilled if we have
$1/\mu_n =o(\sum_{k=0}^{n-1} 1/\mu_k)$. The second requirement is e.g. fulfilled if we have  $\mu_n/\mu_{n-1} \to 1$ as
$\mu_n/\mu_{n-1} \to 1$ as  $n \to \infty$. This latter condition covers a variety of scenarios for
$n \to \infty$. This latter condition covers a variety of scenarios for  $\mu_n$ below exponential growth and above exponential decay.
$\mu_n$ below exponential growth and above exponential decay.
Example 5. In the binary case  $\mathrm P(Y_n=2) = p_n$,
$\mathrm P(Y_n=2) = p_n$,  $\mathrm P(Y_n=0)=1-p_n$ we get
$\mathrm P(Y_n=0)=1-p_n$ we get  $f^{\prime}_{n}(1)= f^{\prime\prime}_{n}(1)=2p_n$. Therefore
$f^{\prime}_{n}(1)= f^{\prime\prime}_{n}(1)=2p_n$. Therefore  $\nu_k/\mu_{k-1}=1/\mu_k$, so that the situation conforms to the previous example.
$\nu_k/\mu_{k-1}=1/\mu_k$, so that the situation conforms to the previous example.
Example 6. In the symmetric case  $\mathrm P(Y_n=0)=\mathrm P(Y_n=2)= p_n/2$ and
$\mathrm P(Y_n=0)=\mathrm P(Y_n=2)= p_n/2$ and  $\mathrm P(Y_n=1)=1-p_n$ we have
$\mathrm P(Y_n=1)=1-p_n$ we have  $\mu_n=1$ and
$\mu_n=1$ and  $\nu_n=p_n$. Here, we find critical or asymptotically degenerate behaviour, according to whether
$\nu_n=p_n$. Here, we find critical or asymptotically degenerate behaviour, according to whether  $\sum_{k=1}^\infty p_n$ is divergent or convergent.
$\sum_{k=1}^\infty p_n$ is divergent or convergent.
Example 7. If the  $Y_n$ take only the values 0 and 1, then all
$Y_n$ take only the values 0 and 1, then all  $\nu_n$ vanish. Now the BPVE is subcritical or asymptotically degenerate, according to whether
$\nu_n$ vanish. Now the BPVE is subcritical or asymptotically degenerate, according to whether  $\mu_n$ converges to zero or to a positive value.
$\mu_n$ converges to zero or to a positive value.
Our proofs rely largely on analytic considerations. The task is to get a grip on the probability measures  $f_1 \circ \cdots \circ f_n$, which are the distributions of the random variables
$f_1 \circ \cdots \circ f_n$, which are the distributions of the random variables  $Z_n$. In order to handle such iterated compositions of generating functions we resort to a device which has been applied from the beginning in the theory of branching processes. For a probability distribution f on
$Z_n$. In order to handle such iterated compositions of generating functions we resort to a device which has been applied from the beginning in the theory of branching processes. For a probability distribution f on  $\mathbb N_0$ with positive, finite mean m we define a function
$\mathbb N_0$ with positive, finite mean m we define a function  $\varphi\,:\,[0,1)\to \mathbb R$ by the equation
$\varphi\,:\,[0,1)\to \mathbb R$ by the equation
 \[\frac 1{1-f(s)} = \frac 1{m(1-s)} + \varphi(s), \qquad 0 \le s \lt 1. \]
\[\frac 1{1-f(s)} = \frac 1{m(1-s)} + \varphi(s), \qquad 0 \le s \lt 1. \]
In this way the mean and the ‘shape’ of f are separated to a certain extent. Indeed, Lemma 1 below shows that  $\varphi$ takes values which are of the size of the standardized second factorial moment
$\varphi$ takes values which are of the size of the standardized second factorial moment  $\nu$. Therefore we briefly name
$\nu$. Therefore we briefly name  $\varphi$ the shape function of f. As we shall see, these functions are useful to dissolve the generating function
$\varphi$ the shape function of f. As we shall see, these functions are useful to dissolve the generating function  $f_1 \circ \cdots \circ f_n$ into a sum (see Lemma 4 below). Here, our contribution consists in obtaining sharp upper and lower bounds for the function
$f_1 \circ \cdots \circ f_n$ into a sum (see Lemma 4 below). Here, our contribution consists in obtaining sharp upper and lower bounds for the function  $\varphi$ and its derivative. The interaction of these bounds then allows for precise estimates e.g. of the survival probabilities
$\varphi$ and its derivative. The interaction of these bounds then allows for precise estimates e.g. of the survival probabilities  $\mathrm P(Z_n \gt 0)$. The role of Assumption (A) in this interplay is to keep both bounds together uniformly in n.
$\mathrm P(Z_n \gt 0)$. The role of Assumption (A) in this interplay is to keep both bounds together uniformly in n.
Concluding this introduction, let us comment on the literature. Agresti in his paper [Reference Agresti1] on almost sure extinction already derived the sharp upper bound for  $\varphi$ which we give below in (8). We note that this bound is related to the well-known Paley–Zygmund inequality (compare the proof of Lemma 7). Agresti also obtained a lower bound for the survival probabilities, which, however, in general is away from our sharp bound. Lyons [Reference Lyons18] obtained the equivalence of conditions (v), (vi), (vii) and (somewhat disguised) (viii) from Theorem 1 under the assumption that the random variables
$\varphi$ which we give below in (8). We note that this bound is related to the well-known Paley–Zygmund inequality (compare the proof of Lemma 7). Agresti also obtained a lower bound for the survival probabilities, which, however, in general is away from our sharp bound. Lyons [Reference Lyons18] obtained the equivalence of conditions (v), (vi), (vii) and (somewhat disguised) (viii) from Theorem 1 under the assumption that the random variables  $Y_n$ are a.s. bounded by a constant, with methods completely different from ours. He also proved Theorem 2, again under the assumption that the offspring numbers are a.s. uniformly bounded by a constant. D’Souza and Biggins [Reference D’Souza and Biggins7] derived Theorem 2 under a different set of assumptions. They required that there are numbers
$Y_n$ are a.s. bounded by a constant, with methods completely different from ours. He also proved Theorem 2, again under the assumption that the offspring numbers are a.s. uniformly bounded by a constant. D’Souza and Biggins [Reference D’Souza and Biggins7] derived Theorem 2 under a different set of assumptions. They required that there are numbers  $a>0$,
$a>0$,  $b>1$ such that
$b>1$ such that  $\mu_{m+n}/\mu_m \ge ab^n$ for all
$\mu_{m+n}/\mu_m \ge ab^n$ for all  $m,n \ge 1$ (called the uniform supercritical case). They did not need finite second moments, but assumed instead that the random variables
$m,n \ge 1$ (called the uniform supercritical case). They did not need finite second moments, but assumed instead that the random variables  $Y_n$ are uniformly dominated by a random variable Y with
$Y_n$ are uniformly dominated by a random variable Y with  $\mathrm E[Y\log^+ Y] \lt \infty$. Goettge [Reference Goettge12] obtained
$\mathrm E[Y\log^+ Y] \lt \infty$. Goettge [Reference Goettge12] obtained  $\mathrm E [W]=1$ under the condition
$\mathrm E [W]=1$ under the condition  $\mu_n \ge an^b$ with
$\mu_n \ge an^b$ with  $a>0$,
$a>0$,  $b>1$ (together with a uniform domination assumption), but did not consider the validity of the equation
$b>1$ (together with a uniform domination assumption), but did not consider the validity of the equation  $\mathrm P(W=0)=q$. In order to prove the conditional limit law from Theorem 4, Jagers [Reference Jagers15] drew attention to uniform estimates due to Sevast’yanov [Reference Sevast’yanov21] (see also [Reference Fahady, Quine and Vere Jones9, Lemma 3]). This approach demands, amongst others, the strong assumption that the sequence
$\mathrm P(W=0)=q$. In order to prove the conditional limit law from Theorem 4, Jagers [Reference Jagers15] drew attention to uniform estimates due to Sevast’yanov [Reference Sevast’yanov21] (see also [Reference Fahady, Quine and Vere Jones9, Lemma 3]). This approach demands, amongst others, the strong assumption that the sequence  $\mathrm E[Z_n]$,
$\mathrm E[Z_n]$,  $n \ge0$, is bounded from above and away from zero. Independently, and in parallel to our work, Bhattacharya and Perlman [Reference Bhattacharya and Perlman3] have presented a considerable generalization of Jager’s result, on a different route and under assumptions which are stronger than ours. For recent results on almost sure extinction and asymptotic exponentiality of multitype BPVEs we refer to [Reference Dolgopyat, Hebbar, Koralov and Perlman8].
$n \ge0$, is bounded from above and away from zero. Independently, and in parallel to our work, Bhattacharya and Perlman [Reference Bhattacharya and Perlman3] have presented a considerable generalization of Jager’s result, on a different route and under assumptions which are stronger than ours. For recent results on almost sure extinction and asymptotic exponentiality of multitype BPVEs we refer to [Reference Dolgopyat, Hebbar, Koralov and Perlman8].
The remainder of this paper is organized as follows. In Section 2 we discuss the assumptions and several examples. In Section 3 we analyze the shape function  $\varphi$. Section 4 contains the proofs of our theorems.
$\varphi$. Section 4 contains the proofs of our theorems.
2. Examples
The following example illustrates the difference in range of the conditions (A) and (B).
Example 8. Let Y have a linear fractional distribution, meaning that
 \[ \mathrm P(Y=y \mid Y\ge 1)= (1-p)^{y-1}p, \qquad y \ge 1 , \]
\[ \mathrm P(Y=y \mid Y\ge 1)= (1-p)^{y-1}p, \qquad y \ge 1 , \]with some  $0<p<1$ and some probability
$0<p<1$ and some probability  $\mathrm P(Y\ge 1)$. Then, from properties of geometric distributions, we have
$\mathrm P(Y\ge 1)$. Then, from properties of geometric distributions, we have
 \begin{align*}\mathrm E[Y\mid Y \ge 1]= \frac 1p, \quad \mathrm E[Y-1\mid Y \ge 1] =\frac {(1-p)}p , \quad \mathrm E[Y(Y-1)\mid Y\ge 1]= \frac{2(1-p)}{p^2},\end{align*}
\begin{align*}\mathrm E[Y\mid Y \ge 1]= \frac 1p, \quad \mathrm E[Y-1\mid Y \ge 1] =\frac {(1-p)}p , \quad \mathrm E[Y(Y-1)\mid Y\ge 1]= \frac{2(1-p)}{p^2},\end{align*}and it follows that
 \begin{align*}\mathrm E[ Y^2;\, Y \ge 2 ] &\le 2 \mathrm E[Y(Y-1)]=\frac{4(1-p)}{p^2} \mathrm P(Y \ge 1) \\&= 4 \, \mathrm E[Y-1;Y \ge 1] \cdot \mathrm E[Y\mid Y \ge 1] \le 4\, \mathrm E[(Y;Y \ge 2] \cdot \mathrm E[Y\mid Y \ge 1].\end{align*}
\begin{align*}\mathrm E[ Y^2;\, Y \ge 2 ] &\le 2 \mathrm E[Y(Y-1)]=\frac{4(1-p)}{p^2} \mathrm P(Y \ge 1) \\&= 4 \, \mathrm E[Y-1;Y \ge 1] \cdot \mathrm E[Y\mid Y \ge 1] \le 4\, \mathrm E[(Y;Y \ge 2] \cdot \mathrm E[Y\mid Y \ge 1].\end{align*}
Thus, for any sequence  $Y_n$ of linear fractional random variables, Assumption (A) is fulfilled with
$Y_n$ of linear fractional random variables, Assumption (A) is fulfilled with  $c=4$, whatever the parameters
$c=4$, whatever the parameters  $p_n$ and
$p_n$ and  $\mathrm P(Y_n \ge 1)$ are.
$\mathrm P(Y_n \ge 1)$ are.
However, for condition (B) the corresponding statement fails. To see this we resort for linear fractional distributions to the formula
 \[\frac{2(1-p_n)}{p_n^2} \mathrm P(Y_n\ge 1)=\mathrm E[Y_n(Y_n-1)] \le \mathrm E[Y_n^2;\, Y_n \ge 2].\]
\[\frac{2(1-p_n)}{p_n^2} \mathrm P(Y_n\ge 1)=\mathrm E[Y_n(Y_n-1)] \le \mathrm E[Y_n^2;\, Y_n \ge 2].\]If we assume (B), then the inequality (6) is also valid, yielding
 \[\frac{2(1-p_n)}{p_n^2} \mathrm P(Y_n\ge 1) \le 4 c_{1/2} \mathrm E[ Y_n-1;\, Y_n\ge 1] \cdot (1+ \mathrm E[Y_n]). \]
\[\frac{2(1-p_n)}{p_n^2} \mathrm P(Y_n\ge 1) \le 4 c_{1/2} \mathrm E[ Y_n-1;\, Y_n\ge 1] \cdot (1+ \mathrm E[Y_n]). \]For linear fractional distributions this estimate may be rewritten as
 \[\frac{2(1-p_n)}{p_n^2} \mathrm P(Y_n\ge 1) \le 4 c_{1/2} \frac {(1-p_n)}{p_n}\mathrm P(Y_n \ge 1)\bigg(1+ \frac 1p_n \mathrm P(Y_n \ge 1)\bigg) , \]
\[\frac{2(1-p_n)}{p_n^2} \mathrm P(Y_n\ge 1) \le 4 c_{1/2} \frac {(1-p_n)}{p_n}\mathrm P(Y_n \ge 1)\bigg(1+ \frac 1p_n \mathrm P(Y_n \ge 1)\bigg) , \]which simplifies to
 \[ \frac 1{2c_{1/2}} \le p_n + \mathrm P(Y_n \ge 1). \]
\[ \frac 1{2c_{1/2}} \le p_n + \mathrm P(Y_n \ge 1). \]
Thus, condition (B) implies  $\inf_n (p_n + \mathrm P(Y_n \ge 1)) \gt 0$, and a sequence of linear fractional random variables satisfying
$\inf_n (p_n + \mathrm P(Y_n \ge 1)) \gt 0$, and a sequence of linear fractional random variables satisfying  $p_n + \mathrm P(Y_n \ge 1)\le1/n$ does not meet (B).
$p_n + \mathrm P(Y_n \ge 1)\le1/n$ does not meet (B).
Incidentally, Theorem 4 still holds true for linear fractional  $Y_n$,
$Y_n$,  $n \ge 1$, regardless of the validity of (B). Then, as is well known,
$n \ge 1$, regardless of the validity of (B). Then, as is well known,  $Z_n$ is also linear fractional for any
$Z_n$ is also linear fractional for any  $n \ge 1$, and consequently the sequence
$n \ge 1$, and consequently the sequence  $Z_n/ \mathrm E[Z_n \mid Z_n\ge 1]$ given the events that
$Z_n/ \mathrm E[Z_n \mid Z_n\ge 1]$ given the events that  $Z_n \ge 1$ converges in distribution to a standard exponential distribution provided that we have
$Z_n \ge 1$ converges in distribution to a standard exponential distribution provided that we have  $\mathrm E[Z_n \mid Z_n\ge 1] \to \infty$.
$\mathrm E[Z_n \mid Z_n\ge 1] \to \infty$.
In other examples, a direct verification of Assumptions (A) or (B) can be cumbersome. Therefore we introduce another assumption, which is often easier to handle: there is a constant  $\skew2\bar{c} \lt \infty$ such that, for all natural numbers
$\skew2\bar{c} \lt \infty$ such that, for all natural numbers  $n \ge 1$,
$n \ge 1$,
 \begin{align} \mathrm E[Y_n(Y_n-1)(Y_n-2)] \le \skew2\bar{c}\, \mathrm E[Y_n(Y_n-1)] \cdot(1+ \mathrm E[Y_n]). \tag{C}\end{align}
\begin{align} \mathrm E[Y_n(Y_n-1)(Y_n-2)] \le \skew2\bar{c}\, \mathrm E[Y_n(Y_n-1)] \cdot(1+ \mathrm E[Y_n]). \tag{C}\end{align}Condition (C) implies (A) and (B), as seen from the following proposition.
Proposition 2. If condition (C) is fulfilled, then (B) holds with  $c_\varepsilon \,:\!=\max(3,5\skew2\bar{c}/\varepsilon)$and (A) holds with
$c_\varepsilon \,:\!=\max(3,5\skew2\bar{c}/\varepsilon)$and (A) holds with  $c\,:\!=\max (12,40 \skew2\bar{c})$.
$c\,:\!=\max (12,40 \skew2\bar{c})$.
Proof. From  $c_\varepsilon \ge 3$ and (C) we obtain
$c_\varepsilon \ge 3$ and (C) we obtain
 \begin{align*}\mathrm E[ Y_n^2;\, Y_n \gt c_\varepsilon(1+ \mathrm E[Y_n])] &\le 5\, \mathrm E[(Y_n-1)(Y_n-2);\, Y_n \gt c_\varepsilon(1+ \mathrm E[Y_n])] \\&\le 5\, \frac {\mathrm E[Y_n(Y_n-1)(Y_n-2)]}{c_\varepsilon(1+ \mathrm E[Y_n])} \\&\le \frac {5\skew2\bar{c}}{c_\varepsilon} \, \mathrm E[Y_n(Y_n-1)].\end{align*}
\begin{align*}\mathrm E[ Y_n^2;\, Y_n \gt c_\varepsilon(1+ \mathrm E[Y_n])] &\le 5\, \mathrm E[(Y_n-1)(Y_n-2);\, Y_n \gt c_\varepsilon(1+ \mathrm E[Y_n])] \\&\le 5\, \frac {\mathrm E[Y_n(Y_n-1)(Y_n-2)]}{c_\varepsilon(1+ \mathrm E[Y_n])} \\&\le \frac {5\skew2\bar{c}}{c_\varepsilon} \, \mathrm E[Y_n(Y_n-1)].\end{align*}It follows that
 \[ \mathrm E[ Y_n^2;\, Y_n \gt c_\varepsilon(1+ \mathrm E[Y_n])] \le \varepsilon \, \mathrm E[Y_n^2;\, Y_n \ge 2] ,\]
\[ \mathrm E[ Y_n^2;\, Y_n \gt c_\varepsilon(1+ \mathrm E[Y_n])] \le \varepsilon \, \mathrm E[Y_n^2;\, Y_n \ge 2] ,\]which is our first claim. The second one follows by means of (6).
Condition (C) can be easily handled by means of generating functions and their derivatives. Here are some examples.
Example 9. If the  $Y_n$ are a.s. uniformly bounded by a constant c, then (C) is satisfied with
$Y_n$ are a.s. uniformly bounded by a constant c, then (C) is satisfied with  $\skew2\bar{c}=c$.
$\skew2\bar{c}=c$.
Example 10. Let Y be Poisson with parameter  $\lambda \gt 0$. Then
$\lambda \gt 0$. Then
 \[ \mathrm E[Y(Y-1)(Y-2)] = \lambda^3 \le \lambda^2(\lambda +1)= \mathrm E[Y(Y-1)](1+\mathrm E[Y]). \]
\[ \mathrm E[Y(Y-1)(Y-2)] = \lambda^3 \le \lambda^2(\lambda +1)= \mathrm E[Y(Y-1)](1+\mathrm E[Y]). \]
Here, (C) is fulfilled with  $\skew2\bar{c}=1$.
$\skew2\bar{c}=1$.
Example 11. For binomial Y with parameters  $m\ge 1$ and
$m\ge 1$ and  $0 \lt p \lt 1$ the situation is analogous, and here
$0 \lt p \lt 1$ the situation is analogous, and here
 \begin{align*} \mathrm E[Y(Y-1)(Y-2)]= m(m-1)(m-2)p^3 \le m(m-1)p^2mp \le\mathrm E[Y(Y-1)](1+ \mathrm E[Y]).\end{align*}
\begin{align*} \mathrm E[Y(Y-1)(Y-2)]= m(m-1)(m-2)p^3 \le m(m-1)p^2mp \le\mathrm E[Y(Y-1)](1+ \mathrm E[Y]).\end{align*}Example 12. For a hypergeometric distribution with parameters (N,K,m) we have, for  $N \ge 3$,
$N \ge 3$,
 \begin{align*}\mathrm E[Y(Y-1)(Y-2)]&=\frac{m(m-1)(m-2)K(K-1)(K-2)}{N(N-1)(N-2)} \\&\le 3\frac{m(m-1) K(K-1) }{N(N-1) }\frac{mK}N \le 3 \mathrm E[Y(Y-1)](1+\mathrm E[Y]) ,\end{align*}
\begin{align*}\mathrm E[Y(Y-1)(Y-2)]&=\frac{m(m-1)(m-2)K(K-1)(K-2)}{N(N-1)(N-2)} \\&\le 3\frac{m(m-1) K(K-1) }{N(N-1) }\frac{mK}N \le 3 \mathrm E[Y(Y-1)](1+\mathrm E[Y]) ,\end{align*}
and (C) is satisfied with  $\skew2\bar{c}=3$. The case
$\skew2\bar{c}=3$. The case  $N \le 2$ can immediately be included.
$N \le 2$ can immediately be included.
Example 13. For negative binomial distributions the generating function is given by
 \[ f(s)= \bigg( \frac p{1-s(1-p)}\bigg)^\alpha \]
\[ f(s)= \bigg( \frac p{1-s(1-p)}\bigg)^\alpha \]
with  $0<p<1$ and a positive integer
$0<p<1$ and a positive integer  $\alpha$. Now,
$\alpha$. Now,
 \begin{align*} \mathrm E[Y] & = \alpha \frac {1-p}p , \\ \mathrm E[Y(Y-1)] & = \alpha(\alpha+1) \frac {(1-p)^2}{p^2}, \\ \mathrm E[Y(Y-1)(Y-2)] & = \alpha(\alpha +1)(\alpha+2) \frac {(1-p)^3}{p^3} .\end{align*}
\begin{align*} \mathrm E[Y] & = \alpha \frac {1-p}p , \\ \mathrm E[Y(Y-1)] & = \alpha(\alpha+1) \frac {(1-p)^2}{p^2}, \\ \mathrm E[Y(Y-1)(Y-2)] & = \alpha(\alpha +1)(\alpha+2) \frac {(1-p)^3}{p^3} .\end{align*}Thus,
 \begin{align*}\mathrm E[Y(Y-1)(Y-2)] \le 3 \mathrm E[Y(Y-1)](1+ \mathrm E[Y]) .\end{align*}
\begin{align*}\mathrm E[Y(Y-1)(Y-2)] \le 3 \mathrm E[Y(Y-1)](1+ \mathrm E[Y]) .\end{align*}
Again, (C) is fulfilled with  $\skew2\bar{c}=3$.
$\skew2\bar{c}=3$.
3. Bounds for the shape function
For  $f \in \mathcal P$ with mean
$f \in \mathcal P$ with mean  $0<m=f^{\prime}(1)<\infty$, define the shape function as the function
$0<m=f^{\prime}(1)<\infty$, define the shape function as the function  $\varphi=\varphi_f\,:\, [0,1) \to \mathbb R$ given by the equation
$\varphi=\varphi_f\,:\, [0,1) \to \mathbb R$ given by the equation
 \[ \frac 1{1-f(s)} = \frac{1}{m(1-s)} + \varphi(s), \qquad 0\le s \lt 1. \]
\[ \frac 1{1-f(s)} = \frac{1}{m(1-s)} + \varphi(s), \qquad 0\le s \lt 1. \]
Due to convexity of f(s) we have  $\varphi(s) \ge 0$ for all
$\varphi(s) \ge 0$ for all  $0\le s \lt 1$. By means of a Taylor expansion of f around 1, one obtains
$0\le s \lt 1$. By means of a Taylor expansion of f around 1, one obtains  $\lim_{s \uparrow 1} \varphi(s) = f^{\prime\prime}(1)/(2f^{\prime}(1)^2) $, and thus we extend
$\lim_{s \uparrow 1} \varphi(s) = f^{\prime\prime}(1)/(2f^{\prime}(1)^2) $, and thus we extend  $\varphi$ by setting
$\varphi$ by setting
 \begin{align} \varphi(1)\,:\!=\frac \nu 2 \quad \text{with}\quad \nu\,:\!= \frac{f^{\prime\prime}(1)}{f^{\prime}(1)^2}.\end{align}
\begin{align} \varphi(1)\,:\!=\frac \nu 2 \quad \text{with}\quad \nu\,:\!= \frac{f^{\prime\prime}(1)}{f^{\prime}(1)^2}.\end{align}In this section we prove the following sharp bounds.
Lemma 1. Assume  $f^{\prime\prime}(1)<\infty$. Then, for
$f^{\prime\prime}(1)<\infty$. Then, for  $0\le s \le 1$,
$0\le s \le 1$,
 \begin{align} \frac 12 \varphi(0) \le \varphi(s) \le 2 \varphi(1) . \end{align}
\begin{align} \frac 12 \varphi(0) \le \varphi(s) \le 2 \varphi(1) . \end{align} Note that  $\varphi$ is identically zero if
$\varphi$ is identically zero if  $f[z]=0$ for all
$f[z]=0$ for all  $z \ge 2$. Otherwise,
$z \ge 2$. Otherwise,  $\varphi(0)>0$ and the lower bound of
$\varphi(0)>0$ and the lower bound of  $\varphi$ becomes strictly positive. Choosing
$\varphi$ becomes strictly positive. Choosing  $s=1$ and
$s=1$ and  $s=0$ in (8), we obtain
$s=0$ in (8), we obtain  $\varphi(0)/2\le \varphi(1)$ and
$\varphi(0)/2\le \varphi(1)$ and  $\varphi(0)\le 2\varphi(1)$. Note that for
$\varphi(0)\le 2\varphi(1)$. Note that for  $f=\delta_k$ (Dirac measure at point k) and
$f=\delta_k$ (Dirac measure at point k) and  $k \ge 2$ we have
$k \ge 2$ we have  $\varphi(1)=\varphi(0)/2$, implying that the constants 1/2 and 2 in (8) cannot be improved. The upper bound was derived in [Reference Geiger and Kersting11] using a different method of proof.
$\varphi(1)=\varphi(0)/2$, implying that the constants 1/2 and 2 in (8) cannot be improved. The upper bound was derived in [Reference Geiger and Kersting11] using a different method of proof.
The next lemma is based on a close investigation of the derivative of  $\varphi(s)$.
$\varphi(s)$.
Lemma 2. Let Y be a random variable with distribution f and assume  $ f^{\prime\prime}(1) \lt \infty$. Then, for
$ f^{\prime\prime}(1) \lt \infty$. Then, for  $0 \le s \le 1$and natural numbers
$0 \le s \le 1$and natural numbers  $a\ge 1$,
$a\ge 1$,
 \[ \sup_{s \le t \le 1}| \varphi(1)-\varphi(t)| \le 2 m\nu^2 (1-s)+2a\nu (1-s)+ \frac 2{m^2}\mathrm E[Y^2;\, Y \gt a] . \]
\[ \sup_{s \le t \le 1}| \varphi(1)-\varphi(t)| \le 2 m\nu^2 (1-s)+2a\nu (1-s)+ \frac 2{m^2}\mathrm E[Y^2;\, Y \gt a] . \] Uniform estimates of  $\varphi(1)-\varphi(s)$ based on third moments have already been obtained by Sevast’yanov [Reference Sevast’yanov21] and others (see [Reference Fahady, Quine and Vere Jones9, Lemma 3]). Our lemma implies and generalizes these estimates. For the proof of these lemmas we use the following result.
$\varphi(1)-\varphi(s)$ based on third moments have already been obtained by Sevast’yanov [Reference Sevast’yanov21] and others (see [Reference Fahady, Quine and Vere Jones9, Lemma 3]). Our lemma implies and generalizes these estimates. For the proof of these lemmas we use the following result.
Lemma 3. Let  $g_1,g_2$be elements of
$g_1,g_2$be elements of  $\mathcal P $with the same support and satisfying the following property. For any
$\mathcal P $with the same support and satisfying the following property. For any  $y\in \mathbb N_0$with
$y\in \mathbb N_0$with  $g_1[y]>0$we have
$g_1[y]>0$we have
 \[ \frac {g_1[z]}{g_1[y]} \le \frac {g_2[z]}{g_2[y]} \qquad \text{for all } z>y . \]
\[ \frac {g_1[z]}{g_1[y]} \le \frac {g_2[z]}{g_2[y]} \qquad \text{for all } z>y . \]Also, let  $\alpha\,:\, \mathbb N_0 \to \mathbb R$be a non-decreasing function. Then
$\alpha\,:\, \mathbb N_0 \to \mathbb R$be a non-decreasing function. Then
 \[ \sum_{y=0}^\infty \alpha(y) g_1[y] \le \sum_{y=0}^\infty \alpha(y) g_2[y] . \]
\[ \sum_{y=0}^\infty \alpha(y) g_1[y] \le \sum_{y=0}^\infty \alpha(y) g_2[y] . \] Proof. The lemma’s assumption is called the ‘monotone likelihood ratio property’, which is known to imply our claim. For convenience, we give a short proof. By assumption there is a non-decreasing function h(y),  $y \in \mathbb N_0$, such that
$y \in \mathbb N_0$, such that  $h(y)= g_2(y)/g_1(y)$ for all elements y of the support of
$h(y)= g_2(y)/g_1(y)$ for all elements y of the support of  $g_1$. Then, for any real number c,
$g_1$. Then, for any real number c,
 \begin{align*} \sum_{y=0}^\infty \alpha(y) g_2[y]- \sum_{y=0}^\infty \alpha(y) g_1[y] &= \sum_{y=0}^\infty (\alpha(y)-c)(g_2[y]-g_1[y]) \\&= \sum_{y=0}^\infty (\alpha(y)-c)(h(y)-1) g_1[y] .\end{align*}
\begin{align*} \sum_{y=0}^\infty \alpha(y) g_2[y]- \sum_{y=0}^\infty \alpha(y) g_1[y] &= \sum_{y=0}^\infty (\alpha(y)-c)(g_2[y]-g_1[y]) \\&= \sum_{y=0}^\infty (\alpha(y)-c)(h(y)-1) g_1[y] .\end{align*}
For  $c\,:\!= \min\{ \alpha(y)\,:\, h(y) \ge 1\}$ we have
$c\,:\!= \min\{ \alpha(y)\,:\, h(y) \ge 1\}$ we have  $\alpha(0) \le c \lt \infty$. For this choice of c, since h and
$\alpha(0) \le c \lt \infty$. For this choice of c, since h and  $\alpha$ are non-decreasing, every summand of the right-hand sum is non-negative. Thus, the whole sum is non-negative, too, and our assertion follows.
$\alpha$ are non-decreasing, every summand of the right-hand sum is non-negative. Thus, the whole sum is non-negative, too, and our assertion follows.
Proof of Lemma 1. (i) First, we examine a special case of Lemma 3. Consider for  $0 \lt s \le 1$ and
$0 \lt s \le 1$ and  $r \in \mathbb N_0$ the probability measures
$r \in \mathbb N_0$ the probability measures
 \begin{align*} g_s[y]= \frac {s^{r-y}}{1+ s+ \cdots+ s^{r}} , \qquad 0\le y \le r .\end{align*}
\begin{align*} g_s[y]= \frac {s^{r-y}}{1+ s+ \cdots+ s^{r}} , \qquad 0\le y \le r .\end{align*}
Then, for  $0 \lt s \le t\le 1$,
$0 \lt s \le t\le 1$,  $0 \le y \lt z\le r$ we have
$0 \le y \lt z\le r$ we have  $g_s[z ]/g_s[y]=s^{y-z}\ge t^{y-z}= g_t[z]/g_t[y]$. Hence, we obtain that
$g_s[z ]/g_s[y]=s^{y-z}\ge t^{y-z}= g_t[z]/g_t[y]$. Hence, we obtain that
 \begin{align*} \sum_{y=0}^r yg_s[y]= \frac{s^{r-1}+2 s^{r-2} + \cdots + r}{1+ s+ \cdots+ s^{r}}\end{align*}
\begin{align*} \sum_{y=0}^r yg_s[y]= \frac{s^{r-1}+2 s^{r-2} + \cdots + r}{1+ s+ \cdots+ s^{r}}\end{align*}
is a decreasing function in s. Also,  $\sum_{y=0}^r yg_0[y] = r$ and
$\sum_{y=0}^r yg_0[y] = r$ and  $\sum_{y=0}^r yg_1[y]= r/2$, and it follows for
$\sum_{y=0}^r yg_1[y]= r/2$, and it follows for  $0\le s \le 1$ that
$0\le s \le 1$ that
 \begin{align} \frac r2 \le \frac{r+(r-1)s+ \cdots + s^{r-1}}{1+ s + \cdots + s^{r}} \le r .\end{align}
\begin{align} \frac r2 \le \frac{r+(r-1)s+ \cdots + s^{r-1}}{1+ s + \cdots + s^{r}} \le r .\end{align} (ii) Next, we derive a second representation for  $\varphi$. We have
$\varphi$. We have
 \[ 1- f(s)= \sum_{z=1}^\infty f[z] (1-s^z) = (1-s) \sum_{z=1}^\infty f[z] \sum_{k=0}^{z-1} s^k \]
\[ 1- f(s)= \sum_{z=1}^\infty f[z] (1-s^z) = (1-s) \sum_{z=1}^\infty f[z] \sum_{k=0}^{z-1} s^k \]and
 \begin{align*} f^{\prime}(1)(1-s)- (1-f(s))&= (1-s) \sum_{z=1}^\infty f [z] \sum_{k=0}^{z-1} (1-s^k) \\& = (1-s)^2 \sum_{z=1}^\infty f [z] \sum_{k=1}^{z-1} \sum_{j=0}^{k-1} s^j \\&= (1-s)^2 \sum_{z=1}^\infty f [z] ((z-1) + (z-2)s + \cdots + s^{z-2}) .\end{align*}
\begin{align*} f^{\prime}(1)(1-s)- (1-f(s))&= (1-s) \sum_{z=1}^\infty f [z] \sum_{k=0}^{z-1} (1-s^k) \\& = (1-s)^2 \sum_{z=1}^\infty f [z] \sum_{k=1}^{z-1} \sum_{j=0}^{k-1} s^j \\&= (1-s)^2 \sum_{z=1}^\infty f [z] ((z-1) + (z-2)s + \cdots + s^{z-2}) .\end{align*}Therefore,
 \begin{align*} \varphi(s) &= \frac{m(1-s)- (1-f(s))}{m(1-s)(1-f(s))} \\&= \frac{\sum_{y=1}^\infty f [y] ((y-1) + (y-2)s + \cdots + s^{y-2})}{m\cdot \sum_{z=1}^\infty f [z] (1+ s + \cdots + s^{z-1})} .\end{align*}
\begin{align*} \varphi(s) &= \frac{m(1-s)- (1-f(s))}{m(1-s)(1-f(s))} \\&= \frac{\sum_{y=1}^\infty f [y] ((y-1) + (y-2)s + \cdots + s^{y-2})}{m\cdot \sum_{z=1}^\infty f [z] (1+ s + \cdots + s^{z-1})} .\end{align*}From (9) it follows that
 \begin{align} \varphi(s) \le \frac{\psi(s)}{m} \le 2\varphi(s) ,\end{align}
\begin{align} \varphi(s) \le \frac{\psi(s)}{m} \le 2\varphi(s) ,\end{align}with
 \[ \psi(s) \,:\!= \frac{\sum_{y=1}^\infty f [y](y-1) (1+ s + \cdots + s^{y-1})}{\sum_{z=1}^\infty f [z] (1+ s + \cdots + s^{z-1})} .\]
\[ \psi(s) \,:\!= \frac{\sum_{y=1}^\infty f [y](y-1) (1+ s + \cdots + s^{y-1})}{\sum_{z=1}^\infty f [z] (1+ s + \cdots + s^{z-1})} .\] Now consider the probability measures  $g_s\in \mathcal P$,
$g_s\in \mathcal P$,  $0\le s \le 1$, given by
$0\le s \le 1$, given by
 \begin{align} g_s[y] \,:\!= \frac {f[y] (1+s+ \cdots + s^{y-1})}{ \sum_{z=1}^\infty f [z ] (1+ s + \cdots + s^{z-1})} , \qquad y \ge 1 .\end{align}
\begin{align} g_s[y] \,:\!= \frac {f[y] (1+s+ \cdots + s^{y-1})}{ \sum_{z=1}^\infty f [z ] (1+ s + \cdots + s^{z-1})} , \qquad y \ge 1 .\end{align}
Then, for  $f[y] \gt 0$ and
$f[y] \gt 0$ and  $z>y$, after some algebra,
$z>y$, after some algebra,
 \[ \frac {g_s[z]}{g_s[y]} = \frac{f[z ]}{f[y ]} \prod_{v=1}^{z-y}\bigg( 1+ \frac 1{s^{-1}+ \cdots + s^{-y-v+1}}\bigg) , \]
\[ \frac {g_s[z]}{g_s[y]} = \frac{f[z ]}{f[y ]} \prod_{v=1}^{z-y}\bigg( 1+ \frac 1{s^{-1}+ \cdots + s^{-y-v+1}}\bigg) , \]
which is an increasing function in s. Therefore, by Lemma 3, the function  $\psi(s)$ is increasing in s. In combination with (10) we get
$\psi(s)$ is increasing in s. In combination with (10) we get
 \[ \varphi(s) \le \frac{\psi(s)}{m} \le \frac{\psi(1)}{m} \le 2 \varphi(1) , \quad 2\varphi(s) \ge \frac{\psi(s)}{m} \ge \frac{\psi(0)}{m} \ge \varphi(0) . \]
\[ \varphi(s) \le \frac{\psi(s)}{m} \le \frac{\psi(1)}{m} \le 2 \varphi(1) , \quad 2\varphi(s) \ge \frac{\psi(s)}{m} \ge \frac{\psi(0)}{m} \ge \varphi(0) . \]This gives the claim of the lemma.
Proof of Lemma 2. First, we estimate the derivative of  $\varphi$, which is given by
$\varphi$, which is given by
 \[ \varphi'(s)= \frac 1m \frac{mf^{\prime}(s)}{(1-f(s))^2} - \frac 1{m(1-s)^2} . \]
\[ \varphi'(s)= \frac 1m \frac{mf^{\prime}(s)}{(1-f(s))^2} - \frac 1{m(1-s)^2} . \]
It turns out that this expression becomes more manageable if we replace the squared geometric mean  $\sqrt{mf^{\prime}(s)}$ on the right-hand side by the square of the arithmetic mean
$\sqrt{mf^{\prime}(s)}$ on the right-hand side by the square of the arithmetic mean  $(m+f^{\prime}(s))/2$. Therefore, we split the derivative into parts according to
$(m+f^{\prime}(s))/2$. Therefore, we split the derivative into parts according to
 \begin{align} \varphi'(s) = \psi_1(s) - \psi_2(s) , \end{align}
\begin{align} \varphi'(s) = \psi_1(s) - \psi_2(s) , \end{align}with
 \[ \psi_1(s)= \frac 1{4m} \frac{(m+f^{\prime}(s))^2}{(1-f(s))^2} - \frac 1{m(1-s)^2} , \quad \psi_2(s)= \frac 1{4 m}\frac{(m+f^{\prime}(s))^2}{(1-f(s))^2} - \frac{f^{\prime}(s)}{(1-f(s))^2} . \]
\[ \psi_1(s)= \frac 1{4m} \frac{(m+f^{\prime}(s))^2}{(1-f(s))^2} - \frac 1{m(1-s)^2} , \quad \psi_2(s)= \frac 1{4 m}\frac{(m+f^{\prime}(s))^2}{(1-f(s))^2} - \frac{f^{\prime}(s)}{(1-f(s))^2} . \]
We show that both  $\psi_1$ and
$\psi_1$ and  $\psi_2$ are non-negative functions, and estimate them from above.
$\psi_2$ are non-negative functions, and estimate them from above.
For  $\psi_1$ we accomplish this task by introducing the function
$\psi_1$ we accomplish this task by introducing the function
 \begin{align*}\zeta(s)&\,:\!= (m+f^{\prime}(s))-2\frac{1-f(s)}{1-s}\\&= \sum_{y = 1}^\infty y(1+s^{y-1})f[y]- 2\sum_{y = 1}^\infty\frac{1-s^y}{1-s} f[y]\\& =\sum_{y = 3}^\infty ( y(1+s^{y-1}) - 2(1+ s+ \cdots + s^{y-1})) f[y] .\end{align*}
\begin{align*}\zeta(s)&\,:\!= (m+f^{\prime}(s))-2\frac{1-f(s)}{1-s}\\&= \sum_{y = 1}^\infty y(1+s^{y-1})f[y]- 2\sum_{y = 1}^\infty\frac{1-s^y}{1-s} f[y]\\& =\sum_{y = 3}^\infty ( y(1+s^{y-1}) - 2(1+ s+ \cdots + s^{y-1})) f[y] .\end{align*}Since
 \begin{align*}\frac {\rm d}{{\rm d}s} (y(1+s^{y-1})& - 2(1+ s+ \cdots + s^{y-1}))\\&= y(y-1)s^{y-2} -2(1+2s + \cdots+ (y-1)s^{y-2})\\&\le y(y-1)s^{y-2} -2s^{y-2}(1+2+ \cdots+ (y-1)) =0\end{align*}
\begin{align*}\frac {\rm d}{{\rm d}s} (y(1+s^{y-1})& - 2(1+ s+ \cdots + s^{y-1}))\\&= y(y-1)s^{y-2} -2(1+2s + \cdots+ (y-1)s^{y-2})\\&\le y(y-1)s^{y-2} -2s^{y-2}(1+2+ \cdots+ (y-1)) =0\end{align*}
for all  $0 \le s \le 1$, and since
$0 \le s \le 1$, and since  $\zeta(1)=0$, we see that
$\zeta(1)=0$, we see that  $\zeta$ is a non-negative, decreasing function. Thus,
$\zeta$ is a non-negative, decreasing function. Thus,  $\psi_1$ is a non-negative function, too. Also,
$\psi_1$ is a non-negative function, too. Also,  $\zeta(0)\le m$.
$\zeta(0)\le m$.
Moreover, we have for  $y \ge 3$ the polynomial identity
$y \ge 3$ the polynomial identity
 \begin{align*}y(1+s^{y-1}) - 2(1+ s+ \cdots + s^{y-1}) = (1-s)^2 \sum_{z=1}^{y-2} z(y-z-1)s^{z-1} ,\end{align*}
\begin{align*}y(1+s^{y-1}) - 2(1+ s+ \cdots + s^{y-1}) = (1-s)^2 \sum_{z=1}^{y-2} z(y-z-1)s^{z-1} ,\end{align*}and consequently
 \[\zeta(s)= (1-s)^2 \xi(s) \]
\[\zeta(s)= (1-s)^2 \xi(s) \]with
 \[ \xi(s)\,:\!= \sum_{y=3}^\infty \sum_{z=1}^{y-2} z(y-z-1)s^{z-1}f[y] .\]
\[ \xi(s)\,:\!= \sum_{y=3}^\infty \sum_{z=1}^{y-2} z(y-z-1)s^{z-1}f[y] .\]
The function  $\xi $ is non-negative and increasing.
$\xi $ is non-negative and increasing.
Coming back to  $\psi_1$, we rewrite it as
$\psi_1$, we rewrite it as
 \[\psi_1(s)= \frac{\frac 12 (m+f^{\prime}(s))(1-s) -(1-f(s))}{(1-f(s))(1-s)}\cdot\frac{\frac 12 (m+f^{\prime}(s))(1-s) +(1-f(s))}{m(1-f(s))(1-s)} .\]
\[\psi_1(s)= \frac{\frac 12 (m+f^{\prime}(s))(1-s) -(1-f(s))}{(1-f(s))(1-s)}\cdot\frac{\frac 12 (m+f^{\prime}(s))(1-s) +(1-f(s))}{m(1-f(s))(1-s)} .\]
Using  $f^{\prime}(s)\le m$, it follows that
$f^{\prime}(s)\le m$, it follows that
 \begin{align*}\psi_1(s)& \le \frac {\zeta(s)}{2(1-f(s))} \bigg(\frac 1{1-f(s)} +\frac 1{m(1-s)}\bigg)\\& = \frac {\zeta(s)}{2 } \bigg( \frac 1{m(1-s)} + \varphi(s)\bigg)\bigg( \frac 2{m(1-s)}+ \varphi(s)\bigg)\\& \le \ 2\zeta(s) \bigg( \frac 1{m^2(1-s)^2} + \varphi(s)^2 \bigg) \\&= \frac{2 \xi(s)}{m^2} + 2 \zeta(s) \varphi(s)^2 .\end{align*}
\begin{align*}\psi_1(s)& \le \frac {\zeta(s)}{2(1-f(s))} \bigg(\frac 1{1-f(s)} +\frac 1{m(1-s)}\bigg)\\& = \frac {\zeta(s)}{2 } \bigg( \frac 1{m(1-s)} + \varphi(s)\bigg)\bigg( \frac 2{m(1-s)}+ \varphi(s)\bigg)\\& \le \ 2\zeta(s) \bigg( \frac 1{m^2(1-s)^2} + \varphi(s)^2 \bigg) \\&= \frac{2 \xi(s)}{m^2} + 2 \zeta(s) \varphi(s)^2 .\end{align*}
By means of Lemma 1, by the monotonicity properties of  $\xi$ and
$\xi$ and  $\zeta$, and by
$\zeta$, and by  $\varphi(1)=\nu/2$,
$\varphi(1)=\nu/2$,  $\zeta(0)\le m$, we obtain
$\zeta(0)\le m$, we obtain
 \begin{align} 0\le \psi_1(s) \le \frac{ 2\xi(s)}{m^2} + 2m \nu^2 . \end{align}
\begin{align} 0\le \psi_1(s) \le \frac{ 2\xi(s)}{m^2} + 2m \nu^2 . \end{align} Now we investigate the function  $\psi_2$, which we rewrite as
$\psi_2$, which we rewrite as
 \[ \psi_2(s)= \frac 1{4m} \bigg(\frac{m-f^{\prime}(s)}{1-f(s)}\bigg)^2 . \]
\[ \psi_2(s)= \frac 1{4m} \bigg(\frac{m-f^{\prime}(s)}{1-f(s)}\bigg)^2 . \]We have
 \[ 1-f(s)= \sum_{z=1}^\infty (1-s^z)f[z]= (1-s)\sum_{z=1}^\infty(1+s+ \cdots + s^{z-1})f[z] \]
\[ 1-f(s)= \sum_{z=1}^\infty (1-s^z)f[z]= (1-s)\sum_{z=1}^\infty(1+s+ \cdots + s^{z-1})f[z] \]and
 \[ m-f^{\prime}(s)= \sum_{y=1}^\infty (1-s^{y-1})y f[y] = (1-s) \sum_{y=2}^\infty y(1+ \cdots + s^{y-2} )f[y] . \]
\[ m-f^{\prime}(s)= \sum_{y=1}^\infty (1-s^{y-1})y f[y] = (1-s) \sum_{y=2}^\infty y(1+ \cdots + s^{y-2} )f[y] . \]Using the notation from (11) it follows that
 \[ \frac{m-f^{\prime}(s)}{1-f(s)} = \sum_{y=2}^\infty \frac{1+ \cdots + s^{y-2}}{1+ \cdots + s^{y-1}} y g_s[y] \le\sum_{y=2}^\infty y g_s[y] .\]
\[ \frac{m-f^{\prime}(s)}{1-f(s)} = \sum_{y=2}^\infty \frac{1+ \cdots + s^{y-2}}{1+ \cdots + s^{y-1}} y g_s[y] \le\sum_{y=2}^\infty y g_s[y] .\]
As above, we may apply Lemma 3 to the probability measures  $g_s$ and conclude that the right-hand term is increasing with s. Therefore,
$g_s$ and conclude that the right-hand term is increasing with s. Therefore,
 \[ 0\le \frac{m-f^{\prime}(s)}{1-f(s)} \le \sum_{y=2}^\infty y g_1[y] = \frac{\sum_{y=2}^\infty y^2 f[y]}{\sum_{z=1}^\infty z f[z]} \le \frac{2\sum_{y=1}^\infty y(y-1) f[y]}{\sum_{z=1}^\infty z f[z]}= 2m\nu , \]
\[ 0\le \frac{m-f^{\prime}(s)}{1-f(s)} \le \sum_{y=2}^\infty y g_1[y] = \frac{\sum_{y=2}^\infty y^2 f[y]}{\sum_{z=1}^\infty z f[z]} \le \frac{2\sum_{y=1}^\infty y(y-1) f[y]}{\sum_{z=1}^\infty z f[z]}= 2m\nu , \]and hence
 \begin{align} 0 \le \psi_2(s)\le m\nu^2 .\end{align}
\begin{align} 0 \le \psi_2(s)\le m\nu^2 .\end{align} Coming to our claim, note first that owing to the non-negativity of  $\psi_1$ and
$\psi_1$ and  $\psi_2$ we obtain from (12), for any
$\psi_2$ we obtain from (12), for any  $s \le u \le 1$,
$s \le u \le 1$,
 \begin{align*} - \int_s^1 \psi_2(t)\, {\rm d}t \le \varphi(1)-\varphi(u) \le \int_s^1 \psi_1(t)\, {\rm d}t .\end{align*}
\begin{align*} - \int_s^1 \psi_2(t)\, {\rm d}t \le \varphi(1)-\varphi(u) \le \int_s^1 \psi_1(t)\, {\rm d}t .\end{align*}Equations (13) and (14) entail
 \begin{align} -m\nu^2 (1-s) \le \varphi(1)-\varphi(u) \le \frac 2{m^2}\int_s^1 \xi(t)\, {\rm d}t + 2m \nu^2 (1-s) .\end{align}
\begin{align} -m\nu^2 (1-s) \le \varphi(1)-\varphi(u) \le \frac 2{m^2}\int_s^1 \xi(t)\, {\rm d}t + 2m \nu^2 (1-s) .\end{align}
It remains to estimate the right-hand integral. We have, for  $0 \le s \lt 1$,
$0 \le s \lt 1$,
 \begin{align*}\int_s^1\xi(t)\, {\rm d}t &= \sum_{y=3}^\infty \sum_{z=1}^{y-2} (y-z-1)(1-s^{z})f[y] \\& \le (1-s) \sum_{y=3}^\infty(y-2)f[y] \sum_{z=1}^{y-2} \sum_{u=0}^{z-1} s^u \\&= (1-s) \sum_{y=3}^\infty(y-2)f[y] \sum_{u=0}^{y-3}(y-2-u)s^u \\&= (1-s) \sum_{u=0}^\infty s^u \sum_{y=u+3}^\infty (y-2)^2 f[y] .\end{align*}
\begin{align*}\int_s^1\xi(t)\, {\rm d}t &= \sum_{y=3}^\infty \sum_{z=1}^{y-2} (y-z-1)(1-s^{z})f[y] \\& \le (1-s) \sum_{y=3}^\infty(y-2)f[y] \sum_{z=1}^{y-2} \sum_{u=0}^{z-1} s^u \\&= (1-s) \sum_{y=3}^\infty(y-2)f[y] \sum_{u=0}^{y-3}(y-2-u)s^u \\&= (1-s) \sum_{u=0}^\infty s^u \sum_{y=u+3}^\infty (y-2)^2 f[y] .\end{align*}The right-hand sum is monotonically decreasing in u, and therefore for natural numbers a we end up with the estimate
 \begin{align*}\int_s^1 \xi(t)\, {\rm d}t & \le \sum_{y=3}^\infty (y-2)^2 f[y](1-s) \sum_{u=0}^{a-1} s^u + \sum_{y=a+3}^\infty (y-2)^2 f[y](1-s) \sum_{u=a}^\infty s^u\\&\le f^{\prime\prime}(1) a(1-s) + \mathrm E[Y^2;\, Y \gt a] .\end{align*}
\begin{align*}\int_s^1 \xi(t)\, {\rm d}t & \le \sum_{y=3}^\infty (y-2)^2 f[y](1-s) \sum_{u=0}^{a-1} s^u + \sum_{y=a+3}^\infty (y-2)^2 f[y](1-s) \sum_{u=a}^\infty s^u\\&\le f^{\prime\prime}(1) a(1-s) + \mathrm E[Y^2;\, Y \gt a] .\end{align*}Combining this estimate with (15), our claim follows.
Remark 2. We have
 \[ \xi(1)= \sum_{y=3}^\infty \sum_{z=1}^{y-2} z(y-z-1)f[y]= \frac 13 \sum_{y=3}^\infty z(z-1)(z-2)f[z] = \frac {f^{\prime\prime\prime}(1)}3 , \]
\[ \xi(1)= \sum_{y=3}^\infty \sum_{z=1}^{y-2} z(y-z-1)f[y]= \frac 13 \sum_{y=3}^\infty z(z-1)(z-2)f[z] = \frac {f^{\prime\prime\prime}(1)}3 , \]
and hence from (12), (13), (14) and the monotonicity of  $\xi$ for
$\xi$ for  $0 \le s \le 1$,
$0 \le s \le 1$,
 \[ -\frac{f^{\prime\prime}(1)^2}{f^{\prime}(1)^3} \le \varphi'(s) \le \frac{ 2f^{\prime\prime\prime}(1)}{3 f^{\prime}(1)^2} + 2 \frac{f^{\prime\prime}(1)^2}{f^{\prime}(1)^3} . \]
\[ -\frac{f^{\prime\prime}(1)^2}{f^{\prime}(1)^3} \le \varphi'(s) \le \frac{ 2f^{\prime\prime\prime}(1)}{3 f^{\prime}(1)^2} + 2 \frac{f^{\prime\prime}(1)^2}{f^{\prime}(1)^3} . \]The quality of these bounds becomes evident from the observation that
 \[ \varphi'(1) = \frac 16 \frac{f^{\prime\prime\prime}(1)}{f^{\prime}(1)^2} - \frac 14 \frac {f^{\prime\prime}(1)^2}{f^{\prime}(1)^3} , \]
\[ \varphi'(1) = \frac 16 \frac{f^{\prime\prime\prime}(1)}{f^{\prime}(1)^2} - \frac 14 \frac {f^{\prime\prime}(1)^2}{f^{\prime}(1)^3} , \]as follows by means of Taylor expansions of f and fʹ about 1.
4. Proofs of the theorems
First let us consider some formulas for moments. There exists a clear-cut expression for the variance of  $Z_n$ due to Fearn [Reference Fearn10]. It seems to be less noticed that there is a similar appealing formula for the second factorial moment of
$Z_n$ due to Fearn [Reference Fearn10]. It seems to be less noticed that there is a similar appealing formula for the second factorial moment of  $Z_n$, which turns out to be more useful for our purpose.
$Z_n$, which turns out to be more useful for our purpose.
Lemma 4. For a BPVE  $(Z_n)_{n \ge 0}$we have
$(Z_n)_{n \ge 0}$we have
 \begin{align*}\mathrm E[Z_n] = \mu_n , \quad \frac{\mathrm E[Z_n(Z_{n}-1)]}{\mathrm E[Z_n]^2}=\sum_{k=1}^{n} \frac{\nu_{k}}{\mu_{k-1} } .\end{align*}
\begin{align*}\mathrm E[Z_n] = \mu_n , \quad \frac{\mathrm E[Z_n(Z_{n}-1)]}{\mathrm E[Z_n]^2}=\sum_{k=1}^{n} \frac{\nu_{k}}{\mu_{k-1} } .\end{align*} Proof. The proof follows a standard pattern. Let  $v=(\,f_1,f_2, \ldots\!)$ denote a varying environment. For non-negative integers
$v=(\,f_1,f_2, \ldots\!)$ denote a varying environment. For non-negative integers  $k \le n$ let us define the probability measures
$k \le n$ let us define the probability measures
 \[ f_{k,n} \,:\!= f_{k+1} \circ \cdots \circ f_n \]
\[ f_{k,n} \,:\!= f_{k+1} \circ \cdots \circ f_n \]
with the convention  $f_{n,n}= \delta_1$ (the Dirac measure at point 1). We have
$f_{n,n}= \delta_1$ (the Dirac measure at point 1). We have
 \[ f^{\prime}_{k,n}(s)= \prod_{l=k+1}^{n} f^{\prime}_{l}(\,f_{l,n}(s)) , \]
\[ f^{\prime}_{k,n}(s)= \prod_{l=k+1}^{n} f^{\prime}_{l}(\,f_{l,n}(s)) , \]
in particular  $f^{\prime}_{n,n}(s)=1$, and after some rearrangements we have
$f^{\prime}_{n,n}(s)=1$, and after some rearrangements we have
 \begin{align*} f^{\prime\prime}_{k,n}(s) = f^{\prime}_{k,n}(s)^2\sum_{l=k+1}^{n} \frac{f^{\prime\prime}_{l}(\,f_{l,n}(s))}{f^{\prime}_{l}(\,f_{l,n}(s))^2\prod_{j=k+1}^{l-1}f^{\prime}_j(\,f_{j,n}(s))} , \end{align*}
\begin{align*} f^{\prime\prime}_{k,n}(s) = f^{\prime}_{k,n}(s)^2\sum_{l=k+1}^{n} \frac{f^{\prime\prime}_{l}(\,f_{l,n}(s))}{f^{\prime}_{l}(\,f_{l,n}(s))^2\prod_{j=k+1}^{l-1}f^{\prime}_j(\,f_{j,n}(s))} , \end{align*}
in particular  $f^{\prime\prime}_{n,n}(s)=0$. Since the distribution of
$f^{\prime\prime}_{n,n}(s)=0$. Since the distribution of  $Z_n$ is given by
$Z_n$ is given by  $f_{0,n}$, by choosing
$f_{0,n}$, by choosing  $k=0$ and
$k=0$ and  $s=1$ Lemma 4 is proved.
$s=1$ Lemma 4 is proved.
Next, we recall an expansion of the generating function of  $Z_n$ taken from [Reference Jirina16] and [Reference Geiger and Kersting11]. This kind of formula has been used in many investigations of branching processes. Let
$Z_n$ taken from [Reference Jirina16] and [Reference Geiger and Kersting11]. This kind of formula has been used in many investigations of branching processes. Let  $\varphi_n$,
$\varphi_n$,  $ n \ge 1$, be the shape functions of
$ n \ge 1$, be the shape functions of  $f_n$,
$f_n$,  $n \ge 1$. Then, since
$n \ge 1$. Then, since  $f_{k,n}=f_{k+1}\circ f_{k+1,n}$ for
$f_{k,n}=f_{k+1}\circ f_{k+1,n}$ for  $k \lt n$, we have
$k \lt n$, we have
 \[ \frac{ 1}{1-f_{k,n}(s)} = \frac{1}{f^{\prime}_{k+1}(1)(1-f_{k+1,n}(s))} + \varphi_1(\,f_{k+1,n}(s)) .\]
\[ \frac{ 1}{1-f_{k,n}(s)} = \frac{1}{f^{\prime}_{k+1}(1)(1-f_{k+1,n}(s))} + \varphi_1(\,f_{k+1,n}(s)) .\]Iterating the formula we end up with the following identity.
Lemma 5. For  $0\le s \lt 1$,
$0\le s \lt 1$,  $0 \le k \lt n$,
$0 \le k \lt n$,
 \[ \frac{1}{1- f_{k,n}(s)} = \frac {\mu_k}{\mu_n(1-s)}+ \varphi_{k,n}(s) \quad \text{with} \quad \varphi_{k,n}(s)\,:\!= \mu_k\sum_{l=k+1}^n \frac{\varphi_l(\,f_{l,n}(s))}{\mu_{l-1}} , \]
\[ \frac{1}{1- f_{k,n}(s)} = \frac {\mu_k}{\mu_n(1-s)}+ \varphi_{k,n}(s) \quad \text{with} \quad \varphi_{k,n}(s)\,:\!= \mu_k\sum_{l=k+1}^n \frac{\varphi_l(\,f_{l,n}(s))}{\mu_{l-1}} , \]
i.e.  $\varphi_{k,n}$ is the shape function of
$\varphi_{k,n}$ is the shape function of  $f_{k,n}$.
$f_{k,n}$.
In order to estimate survival probabilities, Assumption (A) now comes into play. The next lemma reveals its role.
Lemma 6. Condition (A) is fulfilled if and only if there is a constant  $c' \lt \infty$such that we have
$c' \lt \infty$such that we have  $\varphi_n(1)\le c'\varphi_n(0)$for all
$\varphi_n(1)\le c'\varphi_n(0)$for all  $n \ge 1$.
$n \ge 1$.
Proof. Recall that  $Y_n$ denotes a random variable with distribution
$Y_n$ denotes a random variable with distribution  $f_n$. We have
$f_n$. We have  $\mathrm P(Y_n \ge 2)=0$ if and only if
$\mathrm P(Y_n \ge 2)=0$ if and only if  $\varphi_n(1)= \mathrm E[Y_n(Y_n-1)]/(2\mathrm E[Y_n]^2)=0$. Then both inequalities from (A) and from our lemma are valid for all
$\varphi_n(1)= \mathrm E[Y_n(Y_n-1)]/(2\mathrm E[Y_n]^2)=0$. Then both inequalities from (A) and from our lemma are valid for all  $c \gt 0$ and
$c \gt 0$ and  $c'>0$, respectively. Therefore we may, without loss of generality, assume that
$c'>0$, respectively. Therefore we may, without loss of generality, assume that  $\mathrm P(Y_n \ge 2)>0$ for all
$\mathrm P(Y_n \ge 2)>0$ for all  $n \ge 1$. Then we have
$n \ge 1$. Then we have
 \[ \varphi_n(0) = \frac 1{1-f_n[0]} - \frac 1{f^{\prime}_{n}(1)} = \frac{ \mathrm E[(Y_n-1);\, Y_n \ge 1]}{\mathrm E[Y_n]\mathrm P(Y_n \ge1) } , \]
\[ \varphi_n(0) = \frac 1{1-f_n[0]} - \frac 1{f^{\prime}_{n}(1)} = \frac{ \mathrm E[(Y_n-1);\, Y_n \ge 1]}{\mathrm E[Y_n]\mathrm P(Y_n \ge1) } , \]and therefore, because of (7),
 \[ \frac{\varphi_n(1)}{\varphi_n(0)} = \frac{\mathrm E[Y_n(Y_n-1)]\mathrm P(Y_n \ge1) }{2\mathrm E[(Y_n-1);\, Y_n \ge 1]\mathrm E[Y_n] } . \]
\[ \frac{\varphi_n(1)}{\varphi_n(0)} = \frac{\mathrm E[Y_n(Y_n-1)]\mathrm P(Y_n \ge1) }{2\mathrm E[(Y_n-1);\, Y_n \ge 1]\mathrm E[Y_n] } . \]It is not difficult to see that these expressions are bounded uniformly in n if and only if the same holds true for the terms
 \[\frac{\mathrm E[Y_n^2;\, Y_n \ge 2 ]\mathrm P(Y_n \ge1)} { \mathrm E[Y_n;\, Y_n \ge 2] \mathrm E[Y_{n} ] } ,\]
\[\frac{\mathrm E[Y_n^2;\, Y_n \ge 2 ]\mathrm P(Y_n \ge1)} { \mathrm E[Y_n;\, Y_n \ge 2] \mathrm E[Y_{n} ] } ,\]which in turn is equivalent to condition (A). This gives our claim.
In particular, if  $\varphi_n(1)\le c'\varphi_n(0)$ for all
$\varphi_n(1)\le c'\varphi_n(0)$ for all  $n \ge 1$ then we obtain for the shape functions
$n \ge 1$ then we obtain for the shape functions  $\varphi_{k,n}$ of the generating functions
$\varphi_{k,n}$ of the generating functions  $f_{k,n}$ from Lemma 5, by means of Lemmas 6 and 1,
$f_{k,n}$ from Lemma 5, by means of Lemmas 6 and 1,
 \[ \varphi_{k,n}(1) = \mu_n\sum_{l=k+1}^n \frac{\varphi_l(1)}{\mu_{l-1}} \le c' \mu_n\sum_{l=k+1}^n \frac{\varphi_l(0)}{\mu_{l-1}} \le 2c' \mu_n\sum_{l=k+1}^n \frac{\varphi_l(\,f_{l,n}(0))}{\mu_{l-1}} = 2c'\varphi_{k,n}(0)\]
\[ \varphi_{k,n}(1) = \mu_n\sum_{l=k+1}^n \frac{\varphi_l(1)}{\mu_{l-1}} \le c' \mu_n\sum_{l=k+1}^n \frac{\varphi_l(0)}{\mu_{l-1}} \le 2c' \mu_n\sum_{l=k+1}^n \frac{\varphi_l(\,f_{l,n}(0))}{\mu_{l-1}} = 2c'\varphi_{k,n}(0)\]
for all  $1\le k \le n$. This estimate, together with Lemma 4, proves Remark 1 from Section 1, namely that any subsequence of a regular BPVE is regular, too.
$1\le k \le n$. This estimate, together with Lemma 4, proves Remark 1 from Section 1, namely that any subsequence of a regular BPVE is regular, too.
The next lemma has a forerunner in Agresti’s estimate [Reference Agresti1, Theorem 1].
Lemma 7. Under Assumption (A) there is a  $\gamma>0$such that, for all
$\gamma>0$such that, for all  $n \ge 0$,
$n \ge 0$,
 \[ \frac{\mathrm E[Z_n]^2}{\mathrm E[Z_n^2]} \le \mathrm P(Z_n \gt 0) \le \frac 1 \gamma \frac{\mathrm E[Z_n]^2}{\mathrm E[Z_n^2]} . \]
\[ \frac{\mathrm E[Z_n]^2}{\mathrm E[Z_n^2]} \le \mathrm P(Z_n \gt 0) \le \frac 1 \gamma \frac{\mathrm E[Z_n]^2}{\mathrm E[Z_n^2]} . \] Proof. The left-hand estimate is just the standard Paley–Zygmund inequality. For the right-hand estimate observe that  $\mathrm P(Z_n \gt 0)= 1- f_{0,n}[0]=1-f_{0,n}(0)$. Using Lemma 4 with
$\mathrm P(Z_n \gt 0)= 1- f_{0,n}[0]=1-f_{0,n}(0)$. Using Lemma 4 with  $s=0$ we get the representation
$s=0$ we get the representation
 \begin{align}\frac 1{\mathrm P(Z_n \gt 0)} = \frac 1{\mu_n} + \sum_{k=1}^n \frac {\varphi_k(\,f_{k,n}(0))}{\mu_{k-1} } ,\end{align}
\begin{align}\frac 1{\mathrm P(Z_n \gt 0)} = \frac 1{\mu_n} + \sum_{k=1}^n \frac {\varphi_k(\,f_{k,n}(0))}{\mu_{k-1} } ,\end{align}and hence, by means of Lemma 1,
 \begin{align}\frac 1{\mathrm P(Z_n \gt 0)} \ge \frac 1{\mu_n} + \frac 12 \sum_{k=1}^n \frac {\varphi_k(0)}{\mu_{k-1} } ,\end{align}
\begin{align}\frac 1{\mathrm P(Z_n \gt 0)} \ge \frac 1{\mu_n} + \frac 12 \sum_{k=1}^n \frac {\varphi_k(0)}{\mu_{k-1} } ,\end{align}and, by Assumption (A), Lemma 6 and (7),
 \[\frac 1{\mathrm P(Z_n \gt 0)} \ge \frac 1{\mu_n} + \frac 1{2c'} \sum_{k=1}^n \frac {\varphi_k(1)}{\mu_{k-1} } = \frac 1{\mu_n} + \frac 1{4c'} \sum_{k=1}^n \frac {\nu_k}{\mu_{k-1} } . \]
\[\frac 1{\mathrm P(Z_n \gt 0)} \ge \frac 1{\mu_n} + \frac 1{2c'} \sum_{k=1}^n \frac {\varphi_k(1)}{\mu_{k-1} } = \frac 1{\mu_n} + \frac 1{4c'} \sum_{k=1}^n \frac {\nu_k}{\mu_{k-1} } . \]
Letting  $\gamma\,:\!= \min(1, (4c')^{-1})$, we obtain
$\gamma\,:\!= \min(1, (4c')^{-1})$, we obtain
 \begin{align*}\frac 1{\mathrm P(Z_n \gt 0)} \ge \gamma \bigg(\frac 1{\mu_n} + \sum_{k=1}^n \frac {\nu_k}{\mu_{k-1} }\bigg) .\end{align*}
\begin{align*}\frac 1{\mathrm P(Z_n \gt 0)} \ge \gamma \bigg(\frac 1{\mu_n} + \sum_{k=1}^n \frac {\nu_k}{\mu_{k-1} }\bigg) .\end{align*}On the other hand, Lemma 4 implies that
 \begin{align} \frac{\mathrm E[Z_n^2]}{\mathrm E[Z_n]^2} = \frac{\mathrm E[Z_n(Z_n-1)]}{\mathrm E[Z_n]^2} + \frac 1{\mathrm E[Z_n]} = \sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}} + \frac 1{\mu_n} .\end{align}
\begin{align} \frac{\mathrm E[Z_n^2]}{\mathrm E[Z_n]^2} = \frac{\mathrm E[Z_n(Z_n-1)]}{\mathrm E[Z_n]^2} + \frac 1{\mathrm E[Z_n]} = \sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}} + \frac 1{\mu_n} .\end{align}Combining the last two formulas, our claim follows.
(i) if and only if (ii): Since
 $\lim_{n \to \infty} \mathrm P(Z_n>0) = 1-q$, the equivalence follows from Lemma 7.
$\lim_{n \to \infty} \mathrm P(Z_n>0) = 1-q$, the equivalence follows from Lemma 7.(ii) if and only if (iii): We have
(19)thus, because of (18), \begin{align}\sum_{k=1}^n \frac {\rho_k}{\mu_{k-1}} &= \sum_{k=1}^n \frac{\nu_k+ f_k(1)^{-1}-1}{\mu_{k-1}}\notag \\&= \sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}} + \sum_{k=1}^n \bigg(\frac 1{\mu_k}-\frac 1{\mu_{k-1}}\bigg) = \sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}} + \frac 1{\mu_n} -1 ;\end{align}(20)This gives the claim.
\begin{align}\sum_{k=1}^n \frac {\rho_k}{\mu_{k-1}} &= \sum_{k=1}^n \frac{\nu_k+ f_k(1)^{-1}-1}{\mu_{k-1}}\notag \\&= \sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}} + \sum_{k=1}^n \bigg(\frac 1{\mu_k}-\frac 1{\mu_{k-1}}\bigg) = \sum_{k=1}^n \frac {\nu_k}{\mu_{k-1}} + \frac 1{\mu_n} -1 ;\end{align}(20)This gives the claim. \begin{align} \frac{\mathrm E[Z_n^2]}{\mathrm E[Z_n]^2} = \sum_{k=1}^n \frac {\rho_k}{\mu_{k-1}} +1 .\end{align}
\begin{align} \frac{\mathrm E[Z_n^2]}{\mathrm E[Z_n]^2} = \sum_{k=1}^n \frac {\rho_k}{\mu_{k-1}} +1 .\end{align}(iii) if and only if (iv): This equivalence is an immediate consequence of (19).
(v) if and only if (vi): This implication follows again from Lemma 7.
(vi) if and only if (vii): This is a consequence of (20).
(vii) if and only if (viii): Again, this claim follows from (19).
Remark 3. From (17) it follows that a sufficient condition for almost sure extinction is given by the single requirement  $\sum_{k\ge 1} \varphi_k(0)/\mu_{k-1} = \infty$ (without (A)). This confirms a conjecture of Jirina [Reference Jirina16].
$\sum_{k\ge 1} \varphi_k(0)/\mu_{k-1} = \infty$ (without (A)). This confirms a conjecture of Jirina [Reference Jirina16].
Proof of Theorem 2. Statement (i) is obviously valid. For the first part of statement (ii), note that, from Theorem 1(vi) it follows that  $\sup_{n \ge 0} \mathrm E[W_n^2] \lt \infty$. Therefore the martingale
$\sup_{n \ge 0} \mathrm E[W_n^2] \lt \infty$. Therefore the martingale  $(W_n)_{n \ge 0}$ is bounded in
$(W_n)_{n \ge 0}$ is bounded in  $\mathcal L^2$, implying
$\mathcal L^2$, implying  $\mathrm E[W]=\mathrm E[W_0]=1$ and
$\mathrm E[W]=\mathrm E[W_0]=1$ and  $\mathrm E[W^2] \lt \infty$. From (20) it follows that
$\mathrm E[W^2] \lt \infty$. From (20) it follows that
 \[ \mathrm E[W^2] = \sum_{k=1}^\infty \frac {\rho_k}{\mu_{k-1}} +1 . \]
\[ \mathrm E[W^2] = \sum_{k=1}^\infty \frac {\rho_k}{\mu_{k-1}} +1 . \]This implies (1).
For the proof of the last claim we distinguish two cases. Either  $\mu_n \to r$ with
$\mu_n \to r$ with  $0<r<\infty$, in which case
$0<r<\infty$, in which case  $W_n =Z_n/\mu_n \to Z_\infty/r$ a.s. and consequently
$W_n =Z_n/\mu_n \to Z_\infty/r$ a.s. and consequently  $W=Z_\infty/r$ a.s. and
$W=Z_\infty/r$ a.s. and  $\mathrm P(W=0)= \mathrm P(Z_\infty=0)=q$, or we may assume
$\mathrm P(W=0)= \mathrm P(Z_\infty=0)=q$, or we may assume  $\mu_n \to \infty$ in view of Theorem 1(viii). Also,
$\mu_n \to \infty$ in view of Theorem 1(viii). Also,  $ \{Z_\infty=0\} \subset \{W=0\}$ a.s., and thus it is sufficient to show that
$ \{Z_\infty=0\} \subset \{W=0\}$ a.s., and thus it is sufficient to show that  $\mathrm P(Z_\infty \gt 0, W=0)=0$. First, we estimate
$\mathrm P(Z_\infty \gt 0, W=0)=0$. First, we estimate  $\mathrm P(Z_\infty=0 \mid Z_k=1)$ from below. From Lemmas 5 and 1, for
$\mathrm P(Z_\infty=0 \mid Z_k=1)$ from below. From Lemmas 5 and 1, for  $k \lt n$,
$k \lt n$,
 \[ \frac1{1- \mathrm P(Z_n=0\mid Z_k=1)} = \frac 1{1- f_{k,n}(0)} \ge \frac 12 \mu_k\sum_{l=k+1}^n \frac {\varphi_l(0)}{\mu_{l-1}} , \]
\[ \frac1{1- \mathrm P(Z_n=0\mid Z_k=1)} = \frac 1{1- f_{k,n}(0)} \ge \frac 12 \mu_k\sum_{l=k+1}^n \frac {\varphi_l(0)}{\mu_{l-1}} , \]as well as
 \begin{align*}\frac 1{1- \mathrm E[ {\rm e}^{-\lambda W_n}\mid Z_k=1]} &= \frac 1{1-f_{k,n}({\rm e}^{-\lambda/\mu_n})} \\&\le \frac {\mu_k}{\mu_n(1- {\rm e}^{-\lambda/\mu_n})} + 2 \mu_k\sum_{l=k+1}^n \frac {\varphi_l(1)}{\mu_{l-1}}\end{align*}
\begin{align*}\frac 1{1- \mathrm E[ {\rm e}^{-\lambda W_n}\mid Z_k=1]} &= \frac 1{1-f_{k,n}({\rm e}^{-\lambda/\mu_n})} \\&\le \frac {\mu_k}{\mu_n(1- {\rm e}^{-\lambda/\mu_n})} + 2 \mu_k\sum_{l=k+1}^n \frac {\varphi_l(1)}{\mu_{l-1}}\end{align*}
with  $\lambda \gt 0$. By means of Lemma 4 this entails
$\lambda \gt 0$. By means of Lemma 4 this entails
 \[\frac 1{1- \mathrm E[ {\rm e}^{-\lambda W_n}\mid Z_k=1]} \le \frac {\mu_k}{\mu_n(1- e^{-\lambda/\mu_n})} + \frac{4c'}{1- \mathrm P(Z_n=0\mid Z_k=1)} .\]
\[\frac 1{1- \mathrm E[ {\rm e}^{-\lambda W_n}\mid Z_k=1]} \le \frac {\mu_k}{\mu_n(1- e^{-\lambda/\mu_n})} + \frac{4c'}{1- \mathrm P(Z_n=0\mid Z_k=1)} .\]
Letting  $n \to \infty$ we get
$n \to \infty$ we get
 \[ \frac 1{1- \mathrm E[ {\rm e}^{-\lambda W}\mid Z_k=1]} \le \frac {\mu_k}\lambda +\frac{4c'}{1- \mathrm P(Z_\infty=0\mid Z_k=1)} , \]
\[ \frac 1{1- \mathrm E[ {\rm e}^{-\lambda W}\mid Z_k=1]} \le \frac {\mu_k}\lambda +\frac{4c'}{1- \mathrm P(Z_\infty=0\mid Z_k=1)} , \]
and with  $\lambda \to \infty$,
$\lambda \to \infty$,
 \[ \frac 1{\mathrm P(W>0\mid Z_k=1)} \le \frac{4c'}{\mathrm P(Z_\infty>0 \mid Z_k=1)} . \]
\[ \frac 1{\mathrm P(W>0\mid Z_k=1)} \le \frac{4c'}{\mathrm P(Z_\infty>0 \mid Z_k=1)} . \]
Using  ${\rm e}^{-2x} \le 1-x $ for
${\rm e}^{-2x} \le 1-x $ for  $0 \le x \le 1/2$, it follows for
$0 \le x \le 1/2$, it follows for  $\mathrm P(W>0 \mid Z_k=1) \le (8c')^{-1}$ that
$\mathrm P(W>0 \mid Z_k=1) \le (8c')^{-1}$ that
 \begin{align}\mathrm P(Z_\infty=0\mid Z_k=1) & = 1- \mathrm P(Z_\infty>0\mid Z_k=1) \ge 1- 4c' \mathrm P(W>0\mid Z_k=1)\notag \\ &\ge {\rm e}^{- 8c'\mathrm P(W>0\mid Z_k=1)} \ge (1- \mathrm P(W>0\mid Z_k=1))^{8c'}\notag \\& = \mathrm P(W=0\mid Z_k=1)^{8c'} .\end{align}
\begin{align}\mathrm P(Z_\infty=0\mid Z_k=1) & = 1- \mathrm P(Z_\infty>0\mid Z_k=1) \ge 1- 4c' \mathrm P(W>0\mid Z_k=1)\notag \\ &\ge {\rm e}^{- 8c'\mathrm P(W>0\mid Z_k=1)} \ge (1- \mathrm P(W>0\mid Z_k=1))^{8c'}\notag \\& = \mathrm P(W=0\mid Z_k=1)^{8c'} .\end{align} Now we draw on a martingale which already appears in the work of D’Souza and Biggins [Reference D’Souza and Biggins7]. For  $n \ge 0$, let
$n \ge 0$, let
 \[ M_n \,:\!= \mathrm P(W=0\mid Z_0, \ldots , Z_n) = \mathrm P(W=0\mid Z_n=1)^{Z_n} \text{ a.s.} \]
\[ M_n \,:\!= \mathrm P(W=0\mid Z_0, \ldots , Z_n) = \mathrm P(W=0\mid Z_n=1)^{Z_n} \text{ a.s.} \]
From standard martingale theory  $M_n\to I\{W=0\}$ a.s. In particular, we have
$M_n\to I\{W=0\}$ a.s. In particular, we have
 \begin{align} \mathrm P(W=0\mid Z_n=1)^{Z_n} \to 1 \text{ a.s.\ on the event that } W=0 ,\end{align}
\begin{align} \mathrm P(W=0\mid Z_n=1)^{Z_n} \to 1 \text{ a.s.\ on the event that } W=0 ,\end{align}a result which has already been exploited by D’Souza [Reference D’Souza6].
We distinguish two cases. Either there is an infinite sequence of natural numbers such that  $\mathrm P(W \gt 0 \mid Z_n=1) \gt (8c')^{-1}$ along this sequence, so (22) implies that
$\mathrm P(W \gt 0 \mid Z_n=1) \gt (8c')^{-1}$ along this sequence, so (22) implies that  $Z_n \to 0$ a.s. on the event
$Z_n \to 0$ a.s. on the event  $W=0$, or we may apply our estimate (21) to obtain from (22) that
$W=0$, or we may apply our estimate (21) to obtain from (22) that
 \[ \mathrm P(Z_\infty=0 \mid Z_n=1)^{Z_n} \to 1 \text{ a.s.\ on the event that }W=0 . \]
\[ \mathrm P(Z_\infty=0 \mid Z_n=1)^{Z_n} \to 1 \text{ a.s.\ on the event that }W=0 . \]
Therefore, given  $\varepsilon \gt 0$, we have, for n sufficiently large,
$\varepsilon \gt 0$, we have, for n sufficiently large,
 \begin{align*}\mathrm P(Z_\infty \gt 0, W=0) &\le \varepsilon + \mathrm P(Z_n \gt 0, \mathrm P(Z_\infty=0 \mid Z_n=1)^{Z_n} \ge 1-\varepsilon) \\& \le \varepsilon + \frac 1{1-\varepsilon} \mathrm E [ \mathrm P(Z_\infty=0\mid Z_n);\, Z_n>0] \\&= \varepsilon + \frac 1{1-\varepsilon} \mathrm P(Z_\infty=0, Z_n>0) .\end{align*}
\begin{align*}\mathrm P(Z_\infty \gt 0, W=0) &\le \varepsilon + \mathrm P(Z_n \gt 0, \mathrm P(Z_\infty=0 \mid Z_n=1)^{Z_n} \ge 1-\varepsilon) \\& \le \varepsilon + \frac 1{1-\varepsilon} \mathrm E [ \mathrm P(Z_\infty=0\mid Z_n);\, Z_n>0] \\&= \varepsilon + \frac 1{1-\varepsilon} \mathrm P(Z_\infty=0, Z_n>0) .\end{align*}
Letting  $n \to \infty$ we thus obtain
$n \to \infty$ we thus obtain  $\mathrm P(Z_\infty \gt 0, W=0) \le \varepsilon$; the claim then follows with
$\mathrm P(Z_\infty \gt 0, W=0) \le \varepsilon$; the claim then follows with  $\varepsilon \to 0$.
$\varepsilon \to 0$.
Proof of Theorem 3. We begin with the proof of the last claim. Note that the assertion from Lemma 7 can be rewritten as
 \[ \gamma \frac {\mathrm E[Z_n^2]}{\mathrm E[Z_n]} \le \mathrm E[Z_n \mid Z_n \gt 0] \le \frac {\mathrm E[Z_n^2]}{\mathrm E[Z_n]} , \]
\[ \gamma \frac {\mathrm E[Z_n^2]}{\mathrm E[Z_n]} \le \mathrm E[Z_n \mid Z_n \gt 0] \le \frac {\mathrm E[Z_n^2]}{\mathrm E[Z_n]} , \]
and (18) gives  $ \mathrm E[Z_n^2]/\mathrm E[Z_n]= 1+ \mu_n \sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}}=a_n$. This implies (4).
$ \mathrm E[Z_n^2]/\mathrm E[Z_n]= 1+ \mu_n \sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}}=a_n$. This implies (4).
Consequently, by means of Markov’s inequality we obtain
 \[\mathrm P(Z_n/a_n \gt u \mid Z_n \gt 0) \le \frac 1{ua_n} \mathrm E[Z_n \mid Z_n \gt 0] \le \frac 1u ,\]
\[\mathrm P(Z_n/a_n \gt u \mid Z_n \gt 0) \le \frac 1{ua_n} \mathrm E[Z_n \mid Z_n \gt 0] \le \frac 1u ,\]which implies the theorem’s first claim.
Concerning the second claim we remark that for  $a_n \lt 2$ we may set
$a_n \lt 2$ we may set  $u=1/2$. For
$u=1/2$. For  $a_n \ge 2$ we have, by means of Lemma 5, the estimate
$a_n \ge 2$ we have, by means of Lemma 5, the estimate
 \begin{align*} 1-s^u &+ \mathrm P(Z_n/a_n \gt u) \\&\ge \mathrm E[1- s^{Z_n/a_n}\mid Z_n \gt 0] \mathrm E[ 1-s^{Z_n/a_n}\mid Z_n>0]\\& = \frac{1-f_{0,n}(s^{1/a_n})}{1-f_{0,n}(0)}\\&= \bigg(\frac 1{\mu_n} + \sum_{k=1}^n \frac{\varphi_k(\,f_{k,n}(0))}{\mu_{k-1}}\bigg)\Big/\bigg(\frac 1{\mu_n(1-s^{1/a_n})} + \sum_{k=1}^n \frac{\varphi_k(\,f_{k,n}(s^{1/a_n}))}{\mu_{k-1}}\bigg)\end{align*}
\begin{align*} 1-s^u &+ \mathrm P(Z_n/a_n \gt u) \\&\ge \mathrm E[1- s^{Z_n/a_n}\mid Z_n \gt 0] \mathrm E[ 1-s^{Z_n/a_n}\mid Z_n>0]\\& = \frac{1-f_{0,n}(s^{1/a_n})}{1-f_{0,n}(0)}\\&= \bigg(\frac 1{\mu_n} + \sum_{k=1}^n \frac{\varphi_k(\,f_{k,n}(0))}{\mu_{k-1}}\bigg)\Big/\bigg(\frac 1{\mu_n(1-s^{1/a_n})} + \sum_{k=1}^n \frac{\varphi_k(\,f_{k,n}(s^{1/a_n}))}{\mu_{k-1}}\bigg)\end{align*}
with  $0 \lt s \lt 1$ and
$0 \lt s \lt 1$ and  $u \gt 0$. Lemmas 1 and 6 along with (7) yield the bound
$u \gt 0$. Lemmas 1 and 6 along with (7) yield the bound
 \begin{align*} 1-s^u + \mathrm P(Z_n/a_n \gt u) &\ge \sum_{k=1}^n \frac{\varphi_k(0)}{2\mu_{k-1}}\Big/\bigg(\frac 1{\mu_n(1-s^{1/a_n})} + 2\sum_{k=1}^n \frac{\varphi_k(1)}{\mu_{k-1}}\bigg)\\ &\ge\frac 1{4c'}\sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}}\Big/\bigg(\frac 1{\mu_n(1-s^{1/a_n})} + \sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}}\bigg) .\end{align*}
\begin{align*} 1-s^u + \mathrm P(Z_n/a_n \gt u) &\ge \sum_{k=1}^n \frac{\varphi_k(0)}{2\mu_{k-1}}\Big/\bigg(\frac 1{\mu_n(1-s^{1/a_n})} + 2\sum_{k=1}^n \frac{\varphi_k(1)}{\mu_{k-1}}\bigg)\\ &\ge\frac 1{4c'}\sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}}\Big/\bigg(\frac 1{\mu_n(1-s^{1/a_n})} + \sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}}\bigg) .\end{align*}
Moreover,  $1-s^{1/a_n} \ge a_n^{-1}(1-s) $, since
$1-s^{1/a_n} \ge a_n^{-1}(1-s) $, since  $1/a_n \le 1$. Hence, choosing
$1/a_n \le 1$. Hence, choosing  $s=1/2$ we get
$s=1/2$ we get
 \[1-2^{-u} + \mathrm P(Z_n/a_n \gt u) \ge \frac 1{4c'}\sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}}\Big/\bigg(\frac {2a_n}{\mu_n} + \sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}}\bigg) . \]
\[1-2^{-u} + \mathrm P(Z_n/a_n \gt u) \ge \frac 1{4c'}\sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}}\Big/\bigg(\frac {2a_n}{\mu_n} + \sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}}\bigg) . \]
Finally, from  $a_n\ge 2$ it follows that
$a_n\ge 2$ it follows that  $a_n \le 2 \mu_n \sum_{k=1}^{n} \nu_k/\mu_{k-1}$, and consequently
$a_n \le 2 \mu_n \sum_{k=1}^{n} \nu_k/\mu_{k-1}$, and consequently
 \[ 1-2^{-u} + \mathrm P(Z_n/a_n \gt u) \ge \frac 1{20c'} \]
\[ 1-2^{-u} + \mathrm P(Z_n/a_n \gt u) \ge \frac 1{20c'} \]
for all  $u>0$. If we now set
$u>0$. If we now set  $\theta =1/(40 c')$ and choose
$\theta =1/(40 c')$ and choose  $u>0$ so small that
$u>0$ so small that  $1-2^{-u} \le \theta$ we obtain
$1-2^{-u} \le \theta$ we obtain  $ \mathrm P(Z_n/a_n \gt u) \ge \theta $, which is our second claim.
$ \mathrm P(Z_n/a_n \gt u) \ge \theta $, which is our second claim.
The next lemma prepares the proof of Theorem 4. It clarifies the role of (B).
Lemma 8. Assume condition (B) and let  $q=1$. Then the condition
$q=1$. Then the condition
 \begin{align*} \frac1{\mu_n}= o\bigg(\sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}}\bigg)\end{align*}
\begin{align*} \frac1{\mu_n}= o\bigg(\sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}}\bigg)\end{align*}implies
 \begin{align*} \sup_{0 \le s \le 1}\bigg| \sum_{k=1}^n\frac{ \varphi_k(\,f_{k,n}(s))}{\mu_{k-1}} - \sum_{k=1}^n\frac{\varphi_k(1)}{\mu_{k-1}} \bigg| = o\bigg(\sum_{k=1}^n\frac{ \varphi_k(1)}{\mu_{k-1}}\bigg)\end{align*}
\begin{align*} \sup_{0 \le s \le 1}\bigg| \sum_{k=1}^n\frac{ \varphi_k(\,f_{k,n}(s))}{\mu_{k-1}} - \sum_{k=1}^n\frac{\varphi_k(1)}{\mu_{k-1}} \bigg| = o\bigg(\sum_{k=1}^n\frac{ \varphi_k(1)}{\mu_{k-1}}\bigg)\end{align*}as  $n\to \infty$.
$n\to \infty$.
Proof. Fix  $\varepsilon \gt 0$ and choose
$\varepsilon \gt 0$ and choose  $c_{\varepsilon/9}$ according to Assumption (B). Let
$c_{\varepsilon/9}$ according to Assumption (B). Let
 \[ s_k \,:\!= 1- \frac \eta{1+ f^{\prime}_k(1)} \]
\[ s_k \,:\!= 1- \frac \eta{1+ f^{\prime}_k(1)} \]
with some  $0<\eta \lt 1$. Then, from Lemma 3 with
$0<\eta \lt 1$. Then, from Lemma 3 with  $a= \lfloor c_{\varepsilon/9} \rfloor$,
$a= \lfloor c_{\varepsilon/9} \rfloor$,
 \begin{align*}\sup_{s_k \le t \le 1}|\varphi_k(1)-\varphi_k(t)| \le 2\nu_k\frac{ f^{\prime\prime}_k(1) }{f^{\prime}_k(1)} \frac \eta{ 1+ f^{\prime}_k(1)} +2 c_{\varepsilon/9 } \nu_k \eta + \frac \varepsilon 9 4\nu_k .\end{align*}
\begin{align*}\sup_{s_k \le t \le 1}|\varphi_k(1)-\varphi_k(t)| \le 2\nu_k\frac{ f^{\prime\prime}_k(1) }{f^{\prime}_k(1)} \frac \eta{ 1+ f^{\prime}_k(1)} +2 c_{\varepsilon/9 } \nu_k \eta + \frac \varepsilon 9 4\nu_k .\end{align*}From the estimate in (6) it follows that
 \begin{align}f^{\prime\prime}_k(1) \le 2c_{1/2}f^{\prime}_k(1)(1+ f^{\prime}_k(1)) .\end{align}
\begin{align}f^{\prime\prime}_k(1) \le 2c_{1/2}f^{\prime}_k(1)(1+ f^{\prime}_k(1)) .\end{align}
Therefore there is an  $\eta=\eta_\varepsilon>0$ such that
$\eta=\eta_\varepsilon>0$ such that
 \begin{align} \sup_{s_k \le t \le 1}|\varphi_k(1)-\varphi_k(t)| \le \frac \varepsilon 2 \nu_k =\varepsilon \varphi_k(1) .\end{align}
\begin{align} \sup_{s_k \le t \le 1}|\varphi_k(1)-\varphi_k(t)| \le \frac \varepsilon 2 \nu_k =\varepsilon \varphi_k(1) .\end{align}Now set
 \[ r=r_{\varepsilon,n} \,:\!= \min\{k \le n \,:\, f_{k,n}(0) \le s_k\} . \]
\[ r=r_{\varepsilon,n} \,:\!= \min\{k \le n \,:\, f_{k,n}(0) \le s_k\} . \]
Because of  $f_{n,n}(0)=0$ this minimum is attained. In view of (24) and Lemma 1 it follows that
$f_{n,n}(0)=0$ this minimum is attained. In view of (24) and Lemma 1 it follows that
 \begin{align*} \bigg| \sum_{k=1}^n\frac{ \varphi_k(1)}{\mu_{k-1}} -\sum_{k=1}^n\frac{ \varphi_k(\,f_{k,n}(s))}{\mu_{k-1}} \bigg| \le \varepsilon \sum_{k=1}^{r-1}\frac{ \varphi_k(1)}{\mu_{k-1}} +3 \frac{\varphi_r(1)}{\mu_{r-1}}+ 3\sum_{k=r+1}^n\frac{ \varphi_k(1)}{\mu_{k-1}} .\end{align*}
\begin{align*} \bigg| \sum_{k=1}^n\frac{ \varphi_k(1)}{\mu_{k-1}} -\sum_{k=1}^n\frac{ \varphi_k(\,f_{k,n}(s))}{\mu_{k-1}} \bigg| \le \varepsilon \sum_{k=1}^{r-1}\frac{ \varphi_k(1)}{\mu_{k-1}} +3 \frac{\varphi_r(1)}{\mu_{r-1}}+ 3\sum_{k=r+1}^n\frac{ \varphi_k(1)}{\mu_{k-1}} .\end{align*}From (23) we have
 \begin{align*}\frac{\varphi_r(1)}{\mu_{r-1}}= \frac{f^{\prime\prime}_r(1)}{2f^{\prime}_r(1)^2 \mu_{r-1}} \le \frac{c_{1/2}( f^{\prime}_r(1)+1)}{f^{\prime}_r(1)\mu_{r-1}} = c_{1/2} \bigg( \frac 1{\mu_{r-1}}+\frac 1{\mu_r}\bigg) ,\end{align*}
\begin{align*}\frac{\varphi_r(1)}{\mu_{r-1}}= \frac{f^{\prime\prime}_r(1)}{2f^{\prime}_r(1)^2 \mu_{r-1}} \le \frac{c_{1/2}( f^{\prime}_r(1)+1)}{f^{\prime}_r(1)\mu_{r-1}} = c_{1/2} \bigg( \frac 1{\mu_{r-1}}+\frac 1{\mu_r}\bigg) ,\end{align*}and from Lemma 6,
 \begin{align*}\sum_{k=r+1}^n \frac{ \varphi_k(1)}{\mu_{k-1}} &\le c' \sum_{k=r+1}^n \frac{ \varphi_k(0)}{\mu_{k-1}} \le2 c' \sum_{k=r+1}^n \frac{ \varphi_k(\,f_{k,n}(0))}{\mu_{k-1}} .\end{align*}
\begin{align*}\sum_{k=r+1}^n \frac{ \varphi_k(1)}{\mu_{k-1}} &\le c' \sum_{k=r+1}^n \frac{ \varphi_k(0)}{\mu_{k-1}} \le2 c' \sum_{k=r+1}^n \frac{ \varphi_k(\,f_{k,n}(0))}{\mu_{k-1}} .\end{align*}
From (16) it follows that  $\mathrm P(Z_n>0 \mid Z_r=1)^{-1} =\mu_r/\mu_n+ \mu_r \sum_{k=r+1}^n\varphi_k(\,f_{k,n}(0))/\mu_{k-1}$ for
$\mathrm P(Z_n>0 \mid Z_r=1)^{-1} =\mu_r/\mu_n+ \mu_r \sum_{k=r+1}^n\varphi_k(\,f_{k,n}(0))/\mu_{k-1}$ for  $n>r$, and hence we may proceed to
$n>r$, and hence we may proceed to
 \begin{align*}\sum_{k=r+1}^n \frac{ \varphi_k(1)}{\mu_{k-1}} \le \frac{2c'}{\mu_r(1-f_{r,n}(0))} \le \frac {2c'}{\mu_r (1-s_r)} = \frac{2c'(\,f^{\prime}_r(1)+1)}{\eta\mu_r} = \frac{2c'}{\eta}\bigg( \frac 1{\mu_{r-1}}+\frac 1{\mu_r}\bigg) .\end{align*}
\begin{align*}\sum_{k=r+1}^n \frac{ \varphi_k(1)}{\mu_{k-1}} \le \frac{2c'}{\mu_r(1-f_{r,n}(0))} \le \frac {2c'}{\mu_r (1-s_r)} = \frac{2c'(\,f^{\prime}_r(1)+1)}{\eta\mu_r} = \frac{2c'}{\eta}\bigg( \frac 1{\mu_{r-1}}+\frac 1{\mu_r}\bigg) .\end{align*}Putting our estimates together, we get
 \begin{align} \bigg| \sum_{k=1}^n\frac{ \varphi_k(1)}{\mu_{k-1}} -\sum_{k=1}^n\frac{ \varphi_k(\,f_{k,n}(s))}{\mu_{k-1}} \bigg| \le \varepsilon \sum_{k=1}^{n}\frac{ \varphi_k(1)}{\mu_{k-1}} + 3\bigg( c_{1/2} +\frac{2c'}{\eta}\bigg) \bigg( \frac 1{\mu_{r-1}}+\frac 1{\mu_r}\bigg) .\end{align}
\begin{align} \bigg| \sum_{k=1}^n\frac{ \varphi_k(1)}{\mu_{k-1}} -\sum_{k=1}^n\frac{ \varphi_k(\,f_{k,n}(s))}{\mu_{k-1}} \bigg| \le \varepsilon \sum_{k=1}^{n}\frac{ \varphi_k(1)}{\mu_{k-1}} + 3\bigg( c_{1/2} +\frac{2c'}{\eta}\bigg) \bigg( \frac 1{\mu_{r-1}}+\frac 1{\mu_r}\bigg) .\end{align} Now the assumption  $1/\mu_n=o(\sum_{k=1}^{n} \nu_k/\mu_{k-1})$ comes into play. It implies that there is a positive integer
$1/\mu_n=o(\sum_{k=1}^{n} \nu_k/\mu_{k-1})$ comes into play. It implies that there is a positive integer  $r_\varepsilon$ such that, for all r, n with
$r_\varepsilon$ such that, for all r, n with  $ r_\varepsilon \lt r\le n $,
$ r_\varepsilon \lt r\le n $,
 \begin{align}3\bigg( \frac{2c'}{\eta}+c_{1/2} \bigg) \bigg( \frac 1{\mu_{r-1}}+\frac 1{\mu_r}\bigg) \le \frac \varepsilon 2 \sum_{k=1}^{r-1}\frac{ \nu_k}{\mu_{k-1}}+\frac \varepsilon 2 \sum_{k=1}^{r}\frac{ \nu_k}{\mu_{k-1}} \le \varepsilon \sum_{k=1}^{n}\frac{ \varphi_k(1)}{\mu_{k-1}} .\end{align}
\begin{align}3\bigg( \frac{2c'}{\eta}+c_{1/2} \bigg) \bigg( \frac 1{\mu_{r-1}}+\frac 1{\mu_r}\bigg) \le \frac \varepsilon 2 \sum_{k=1}^{r-1}\frac{ \nu_k}{\mu_{k-1}}+\frac \varepsilon 2 \sum_{k=1}^{r}\frac{ \nu_k}{\mu_{k-1}} \le \varepsilon \sum_{k=1}^{n}\frac{ \varphi_k(1)}{\mu_{k-1}} .\end{align}
Also, from the assumptions that  $q=1$ and
$q=1$ and  $1/\mu_n=o(\sum_{k=1}^{n} \nu_k/\mu_{k-1})$, together with Theorem 1(iv) and (7), we have
$1/\mu_n=o(\sum_{k=1}^{n} \nu_k/\mu_{k-1})$, together with Theorem 1(iv) and (7), we have
 \[ \sum_{k=1}^n\frac{ \varphi_k(1)}{\mu_{k-1}}=\frac 12 \sum_{k=1}^n\frac{ \nu_k}{\mu_{k-1}} \to \infty \]
\[ \sum_{k=1}^n\frac{ \varphi_k(1)}{\mu_{k-1}}=\frac 12 \sum_{k=1}^n\frac{ \nu_k}{\mu_{k-1}} \to \infty \]
as  $n \to \infty$, which implies that (26) holds for all
$n \to \infty$, which implies that (26) holds for all  $r \le r_\varepsilon$ and thus for all
$r \le r_\varepsilon$ and thus for all  $r \le n$, if only n is large enough. Thereby we may combine (25) and (26) to obtain
$r \le n$, if only n is large enough. Thereby we may combine (25) and (26) to obtain
 \[\bigg| \sum_{k=1}^n\frac{ \varphi_k(\,f_{k,n}(s))}{\mu_{k-1}} - \sum_{k=1}^n\frac{ \varphi_k(1)}{\mu_{k-1}} \bigg| \le 2 \varepsilon \sum_{k=1}^{n}\frac{ \varphi_k(1)}{\mu_{k-1}} \]
\[\bigg| \sum_{k=1}^n\frac{ \varphi_k(\,f_{k,n}(s))}{\mu_{k-1}} - \sum_{k=1}^n\frac{ \varphi_k(1)}{\mu_{k-1}} \bigg| \le 2 \varepsilon \sum_{k=1}^{n}\frac{ \varphi_k(1)}{\mu_{k-1}} \]for sufficiently large n. This proves our claim.
Proof of Theorem 4. (i) implies (ii): We argue by contradiction. If assertion (ii) fails, then there is an increasing sequence  $(n_i)_{i\ge 0}$ in
$(n_i)_{i\ge 0}$ in  $\mathbb N$ fulfilling
$\mathbb N$ fulfilling  $\sup_i \mathrm E[Z_{n_i}\mid Z_{n_i}>0] \lt \infty$. From Theorem 3 it follows that the random variables
$\sup_i \mathrm E[Z_{n_i}\mid Z_{n_i}>0] \lt \infty$. From Theorem 3 it follows that the random variables  $Z_{n_i}$,
$Z_{n_i}$,  $i \ge 0$, conditioned on
$i \ge 0$, conditioned on  $Z_{n_i}>0$ are tight. This does not conform with assertion (i), which proves the implication.
$Z_{n_i}>0$ are tight. This does not conform with assertion (i), which proves the implication.
(ii) implies (iii): This implication follows from Theorem 3, since assertion (iii) just states that  $a_n\to \infty$.
$a_n\to \infty$.
(iii) implies (i): For the proof, let
 \[ b_n\,:\!= \frac{\mu_n}2 \sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}} .\]
\[ b_n\,:\!= \frac{\mu_n}2 \sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}} .\]From Lemma 5 we have
 \begin{align*} 1- \mathrm E[ {\rm e}^{-\lambda Z_n/b_n}&\mid Z_n\gt0] = \frac{1-f_{0,n}({\rm e}^{-\lambda/b_n})}{1-f_{0,n}(0)} \\ &=\bigg(\frac 1{\mu_n} + \sum_{k=1}^n \frac{\varphi_k(\,f_{k,n}(0))}{\mu_{k-1}}\bigg) \Big/\bigg(\frac 1{\mu_n(1- {\rm e}^{-\lambda/b_n})} +\sum_{k=1}^n \frac{\varphi_k(\,f_{k,n}({\rm e}^{-\lambda/b_n}))}{\mu_{k-1}}\bigg) .\end{align*}
\begin{align*} 1- \mathrm E[ {\rm e}^{-\lambda Z_n/b_n}&\mid Z_n\gt0] = \frac{1-f_{0,n}({\rm e}^{-\lambda/b_n})}{1-f_{0,n}(0)} \\ &=\bigg(\frac 1{\mu_n} + \sum_{k=1}^n \frac{\varphi_k(\,f_{k,n}(0))}{\mu_{k-1}}\bigg) \Big/\bigg(\frac 1{\mu_n(1- {\rm e}^{-\lambda/b_n})} +\sum_{k=1}^n \frac{\varphi_k(\,f_{k,n}({\rm e}^{-\lambda/b_n}))}{\mu_{k-1}}\bigg) .\end{align*}
Since  $b_n \to \infty$, from Lemma 8 and the theorem’s assumption we have
$b_n \to \infty$, from Lemma 8 and the theorem’s assumption we have
 \begin{align*} 1- \mathrm E[ {\rm e}^{-\lambda Z_n/b_n}&\mid Z_n \gt 0]\\ &=\bigg((1+o(1))\sum_{k=1}^n \frac{\nu_k}{2\mu_{k-1}}\bigg) \Big/\bigg((1+o(1))\frac {b_n}{\lambda\mu_n} +(1+o(1))\sum_{k=1}^n \frac{\nu_k}{2\mu_{k-1}}\bigg)\end{align*}
\begin{align*} 1- \mathrm E[ {\rm e}^{-\lambda Z_n/b_n}&\mid Z_n \gt 0]\\ &=\bigg((1+o(1))\sum_{k=1}^n \frac{\nu_k}{2\mu_{k-1}}\bigg) \Big/\bigg((1+o(1))\frac {b_n}{\lambda\mu_n} +(1+o(1))\sum_{k=1}^n \frac{\nu_k}{2\mu_{k-1}}\bigg)\end{align*}
as  $n \to \infty$. From the definition of
$n \to \infty$. From the definition of  $b_n$ we get
$b_n$ we get
 \[1- \mathrm E[ {\rm e}^{-\lambda Z_n/b_n}\mid Z_n>0] = \frac{\lambda+o(1)}{1+\lambda } .\]
\[1- \mathrm E[ {\rm e}^{-\lambda Z_n/b_n}\mid Z_n>0] = \frac{\lambda+o(1)}{1+\lambda } .\]This implies assertion (i).
Moreover, from (16), Lemma 8 and assertion (iii) it follows that
 \[\frac 1{\mathrm P(Z_n \gt 0)} = \frac 1{\mu_n} + \sum_{k=1}^n \frac {\varphi_k(\,f_{k,n}(0))}{\mu_{k-1} } \sim \frac 12 \sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}} . \]
\[\frac 1{\mathrm P(Z_n \gt 0)} = \frac 1{\mu_n} + \sum_{k=1}^n \frac {\varphi_k(\,f_{k,n}(0))}{\mu_{k-1} } \sim \frac 12 \sum_{k=1}^n \frac{\nu_k}{\mu_{k-1}} . \]This formula give the extra claims, which concludes the proof.
Proposition 1. By Theorem 1(viii) the condition  $q \lt 1$ is equivalent to the requirements of both
$q \lt 1$ is equivalent to the requirements of both  $\sum_{k=1}^\infty \nu_k/\mu_{k-1} \lt \infty$ and
$\sum_{k=1}^\infty \nu_k/\mu_{k-1} \lt \infty$ and  $0 \lt \lim_n \mu_n \le \infty$. As already explained, the division between the supercritical regime and the asymptotically non-degenerate regime corresponds to the cases
$0 \lt \lim_n \mu_n \le \infty$. As already explained, the division between the supercritical regime and the asymptotically non-degenerate regime corresponds to the cases  $\lim_n \mu_n=\infty $ and
$\lim_n \mu_n=\infty $ and  $0 \lt \lim_n \mu_n<\infty$. This gives the first two assertions of the proposition.
$0 \lt \lim_n \mu_n<\infty$. This gives the first two assertions of the proposition.
Next, the critical regime is given by the requirements that both  $\mathrm E[Z_n \mid Z_n>0] \to \infty$ and
$\mathrm E[Z_n \mid Z_n>0] \to \infty$ and  $q=1$. By Theorems 3 and 1(iv) we may equivalently require that
$q=1$. By Theorems 3 and 1(iv) we may equivalently require that  $1/\mu_n =o(\sum_{k=1}^n \nu_k/\mu_{k-1})$ together with either
$1/\mu_n =o(\sum_{k=1}^n \nu_k/\mu_{k-1})$ together with either  $\sum_{k=1}^n \nu_k/\mu_{k-1}=\infty$ or
$\sum_{k=1}^n \nu_k/\mu_{k-1}=\infty$ or  $\mu_n \to 0$. However, the third and the first of these conditions imply the second one, therefore the third condition can be skipped, and we end up with the requirements
$\mu_n \to 0$. However, the third and the first of these conditions imply the second one, therefore the third condition can be skipped, and we end up with the requirements  $1/\mu_n =o(\sum_{k=1}^n \nu_k/\mu_{k-1})$ and
$1/\mu_n =o(\sum_{k=1}^n \nu_k/\mu_{k-1})$ and  $\sum_{k=1}^n \nu_k/\mu_{k-1}=\infty$, as stated in the proposition.
$\sum_{k=1}^n \nu_k/\mu_{k-1}=\infty$, as stated in the proposition.
Finally, the subcritical regime is characterized by the conditions  $\mathrm E[Z_n \mid Z_n \gt 0] \not\to \infty$ and
$\mathrm E[Z_n \mid Z_n \gt 0] \not\to \infty$ and  $q=1$. Because of Theorem 3, the first condition is equivalent to the requirement
$q=1$. Because of Theorem 3, the first condition is equivalent to the requirement  $a_n \not\to \infty$, respectively to
$a_n \not\to \infty$, respectively to  $\liminf_n \mu_n \sum_{k=1}^n \nu_k/\mu_{k-1} \lt \infty$. Moreover,
$\liminf_n \mu_n \sum_{k=1}^n \nu_k/\mu_{k-1} \lt \infty$. Moreover,  $\liminf_n \mu_n=0$ implies
$\liminf_n \mu_n=0$ implies  $q=1$, and therefore the conditions stated in the proposition imply subcriticality. Conversely, if
$q=1$, and therefore the conditions stated in the proposition imply subcriticality. Conversely, if  $q=1$ then by Theorem 1(iv) we have
$q=1$ then by Theorem 1(iv) we have  $\lim_n \mu_n=0$ or
$\lim_n \mu_n=0$ or  $\sum_{k=1}^n \nu_k/\mu_{k-1} \lt \infty$. The former of these conditions trivially yields
$\sum_{k=1}^n \nu_k/\mu_{k-1} \lt \infty$. The former of these conditions trivially yields  $\liminf_n \mu_n=0$, whereas the latter, together with
$\liminf_n \mu_n=0$, whereas the latter, together with  $\liminf_n \mu_n \sum_{k=1}^n \nu_k/\mu_{k-1} \lt \infty$, implies
$\liminf_n \mu_n \sum_{k=1}^n \nu_k/\mu_{k-1} \lt \infty$, implies  $\liminf_n \mu_n=0$. Therefore the two conditions stated in the proposition are also necessary for subcriticality.
$\liminf_n \mu_n=0$. Therefore the two conditions stated in the proposition are also necessary for subcriticality.