Article contents
Zipf’s law for atlas models
Published online by Cambridge University Press: 23 November 2020
Abstract
A set of data with positive values follows a Pareto distribution if the log–log plot of value versus rank is approximately a straight line. A Pareto distribution satisfies Zipf’s law if the log–log plot has a slope of 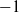 $-1$. Since many types of ranked data follow Zipf’s law, it is considered a form of universality. We propose a mathematical explanation for this phenomenon based on Atlas models and first-order models, systems of strictly positive continuous semimartingales with parameters that depend only on rank. We show that the stationary distribution of an Atlas model will follow Zipf’s law if and only if two natural conditions, conservation and completeness, are satisfied. Since Atlas models and first-order models can be constructed to approximate systems of time-dependent rank-based data, our results can explain the universality of Zipf’s law for such systems. However, ranked data generated by other means may follow non-Zipfian Pareto distributions. Hence, our results explain why Zipf’s law holds for word frequency, firm size, household wealth, and city size, while it does not hold for earthquake magnitude, cumulative book sales, and the intensity of wars, all of which follow non-Zipfian Pareto distributions.
$-1$. Since many types of ranked data follow Zipf’s law, it is considered a form of universality. We propose a mathematical explanation for this phenomenon based on Atlas models and first-order models, systems of strictly positive continuous semimartingales with parameters that depend only on rank. We show that the stationary distribution of an Atlas model will follow Zipf’s law if and only if two natural conditions, conservation and completeness, are satisfied. Since Atlas models and first-order models can be constructed to approximate systems of time-dependent rank-based data, our results can explain the universality of Zipf’s law for such systems. However, ranked data generated by other means may follow non-Zipfian Pareto distributions. Hence, our results explain why Zipf’s law holds for word frequency, firm size, household wealth, and city size, while it does not hold for earthquake magnitude, cumulative book sales, and the intensity of wars, all of which follow non-Zipfian Pareto distributions.
MSC classification
Information
- Type
- Research Papers
- Information
- Copyright
- © Applied Probability Trust 2020
References
- 4
- Cited by


