Hostname: page-component-848d4c4894-2xdlg Total loading time: 0 Render date: 2024-06-16T07:21:28.840Z Has data issue: false hasContentIssue false
  • English
  • Français

(Almost) complete characterization of the stability of a discrete-time Hawkes process with inhibition and memory of length two

Part of: Difference and functional equations Difference equations Inference from stochastic processes Markov processes

Published online by Cambridge University Press:  24 May 2024

Manon Costa Open the ORCID record for Manon Costa [Opens in a new window] ,
Pascal Maillard Open the ORCID record for Pascal Maillard [Opens in a new window]  and
Anthony Muraro
Manon Costa*
Affiliation:
Université de Toulouse
Pascal Maillard*
Affiliation:
Institut Universitaire de France Université de Toulouse
Anthony Muraro*
Affiliation:
Université de Toulouse
*
*Postal address: Institut de Mathématiques de Toulouse, CNRS UMR 5219, Université Toulouse III Paul Sabatier, 118 route de Narbonne, F-31062 Toulouse cedex 09.
*Postal address: Institut de Mathématiques de Toulouse, CNRS UMR 5219, Université Toulouse III Paul Sabatier, 118 route de Narbonne, F-31062 Toulouse cedex 09.
*Postal address: Institut de Mathématiques de Toulouse, CNRS UMR 5219, Université Toulouse III Paul Sabatier, 118 route de Narbonne, F-31062 Toulouse cedex 09.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a Poisson autoregressive process whose parameters depend on the past of the trajectory. We allow these parameters to take negative values, modelling inhibition. More precisely, the model is the stochastic process 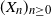$(X_n)_{n\ge0}$ with parameters 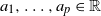$a_1,\ldots,a_p \in \mathbb{R}$, 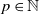$p\in\mathbb{N}$, and 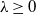$\lambda \ge 0$, such that, for all 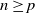$n\ge p$, conditioned on 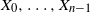$X_0,\ldots,X_{n-1}$, 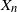$X_n$ is Poisson distributed with parameter 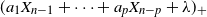$(a_1 X_{n-1} + \cdots + a_p X_{n-p} + \lambda)_+$. This process can be regarded as a discrete-time Hawkes process with inhibition and a memory of length p. In this paper we initiate the study of necessary and sufficient conditions of stability for these processes, which seems to be a hard problem in general. We consider specifically the case 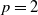$p = 2$, for which we are able to classify the asymptotic behavior of the process for the whole range of parameters, except for boundary cases. In particular, we show that the process remains stochastically bounded whenever the solution to the linear recurrence equation 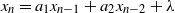$x_n = a_1x_{n-1} + a_2x_{n-2} + \lambda$ remains bounded, but the converse is not true. Furthermore, the criterion for stochastic boundedness is not symmetric in 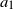$a_1$ and 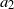$a_2$, in contrast to the case of non-negative parameters, illustrating the complex effects of inhibition.

Keywords

Hawkes processinhibitionMarkov chainautoregressive processergodicityLyapunov functions

MSC classification

Primary: 60J20: Applications of Markov chains and discrete-time Markov processes on general state spaces (social mobility, learning theory, industrial processes, etc.) 62M10: Time series, auto-correlation, regression, etc.
Secondary: 39A30: Stability theory
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 22
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bremaud, P. and Massoulie, L. (1996). Stability of nonlinear Hawkes processes. Ann. Prob. 24, 1563–1588.CrossRefGoogle Scholar
Cattiaux, P., Colombani, L. and Costa, M. (2022). Limit theorems for Hawkes processes including inhibition. Stoch. Process. Appl. 149, 404–426.CrossRefGoogle Scholar
Costa, M., Graham, C., Marsalle, L. and Tran, V.-C. (2020). Renewal in Hawkes processes with self-excitation and inhibition. Adv. Appl. Prob. 52, 879–915.CrossRefGoogle Scholar
Daley, D. J. and Vere-Jones, D. (2006). An Introduction to the Theory of Point Processes. Vol. I, Elementary Theory and Methods. Springer, New York.Google Scholar
Douc, R., Moulines, E., Priouret, P. and Soulier, P. (2018). Markov Chains. Springer, Cham.CrossRefGoogle Scholar
Ferland, R., Latour, A. and Oraichi, D. (2006). Integer-valued GARCH process. J. Time Ser. Anal. 27, 923–942.CrossRefGoogle Scholar
Fokianos, K. and Fried, R. (2010). Interventions in INGARCH processes. J. Time Ser. Anal. 31, 210–225.CrossRefGoogle Scholar
Foster, F. G. (1953). On the stochastic matrices associated with certain queuing processes. Ann. Math. Statist. 24, 355–360.CrossRefGoogle Scholar
Gallier, J. and Quaintance, J. (2020). Linear Algebra and Optimization with Applications to Machine Learning. Vol. I, Linear Algebra for Computer Vision, Robotics, and Machine Learning. World Scientific, Singapore.Google Scholar
Hawkes, A. G. (1971). Spectra of some self-exciting and mutually exciting point processes. Biometrika, 58, 83–90.CrossRefGoogle Scholar
Hawkes, A. G. and Oakes, D. (1974). A cluster process representation of a self-exciting process. J. Appl. Prob. 11, 493–503.CrossRefGoogle Scholar
Kirchner, M. (2016). Hawkes and INAR( $\infty$ ) processes. Stoch. Process. Appl. 126, 2494–2525.CrossRefGoogle Scholar
Meyn, S. P. and Tweedie, R. L. (2009). Markov Chains and Stochastic Stability, 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Raad, M. B. and Löcherbach, E. (2020). Stability for Hawkes processes with inhibition. Electron. Commun. Prob. 25, 1–9.Google Scholar
Seol, Y. (2015). Limit theorems for discrete Hawkes processes. Statist. Prob. Lett. 99, 223–229.CrossRefGoogle Scholar