Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Di Crescenzo, Antonio
Martinucci, Barbara
and
Zacks, Shelemyahu
2015.
Compound Poisson Process with a Poisson Subordinator.
Journal of Applied Probability,
Vol. 52,
Issue. 2,
p.
360.
Polito, Federico
and
Scalas, Enrico
2016.
A generalization of the space-fractional Poisson process and its connection to some Lévy processes.
Electronic Communications in Probability,
Vol. 21,
Issue. none,
Buchak, Khrystyna
and
Sakhno, Lyudmyla
2017.
Compositions of Poisson and Gamma processes.
Modern Stochastics: Theory and Applications,
Vol. 4,
Issue. 2,
p.
161.
Buchak, Khrystyna
and
Sakhno, Lyudmyla
2018.
Properties of Poisson processes directed by compound Poisson-Gamma subordinators.
Modern Stochastics: Theory and Applications,
Vol. 5,
Issue. 2,
p.
167.
Kataria, Kuldeep Kumar
and
Vellaisamy, Palaniappan
2018.
On martingale characterizations for some generalized space fractional Poisson processes.
Stochastic Analysis and Applications,
Vol. 36,
Issue. 4,
p.
665.
Garra, Roberto
Orsingher, Enzo
and
Polito, Federico
2018.
A Note on Hadamard Fractional Differential Equations with Varying Coefficients and Their Applications in Probability.
Mathematics,
Vol. 6,
Issue. 1,
p.
4.
Maheshwari, A.
and
Vellaisamy, P.
2019.
Fractional Poisson Process Time-Changed by Lévy Subordinator and Its Inverse.
Journal of Theoretical Probability,
Vol. 32,
Issue. 3,
p.
1278.
Beghin, Luisa
and
Ricciuti, Costantino
2019.
Time-inhomogeneous fractional Poisson processes defined by the multistable subordinator.
Stochastic Analysis and Applications,
Vol. 37,
Issue. 2,
p.
171.
Sengar, Ayushi S.
Maheshwari, A.
and
Upadhye, N. S.
2020.
Time-changed Poisson processes of order
k
.
Stochastic Analysis and Applications,
Vol. 38,
Issue. 1,
p.
124.
Michelitsch, Thomas M.
Polito, Federico
and
Riascos, Alejandro P.
2020.
Biased Continuous-Time Random Walks with Mittag-Leffler Jumps.
Fractal and Fractional,
Vol. 4,
Issue. 4,
p.
51.
Kataria, Kuldeep Kumar
and
Khandakar, Mostafizar
2021.
Convoluted Fractional Poisson Process
.
Latin American Journal of Probability and Mathematical Statistics,
Vol. 18,
Issue. 1,
p.
1241.
Yakubovich, Yuri
2021.
A simple proof of the Lévy–Khintchine formula for subordinators.
Statistics & Probability Letters,
Vol. 176,
Issue. ,
p.
109136.
Kataria, K. K.
and
Khandakar, M.
2021.
On the Long-Range Dependence of Mixed Fractional Poisson Process.
Journal of Theoretical Probability,
Vol. 34,
Issue. 3,
p.
1607.
Maheshwari, Aditya
and
Singh, Reetendra
2021.
Nonlocal and Fractional Operators.
Vol. 26,
Issue. ,
p.
205.
Kataria, Kuldeep Kumar
and
Khandakar, Mostafizar
2022.
Skellam and time-changed variants of the generalized fractional counting process.
Fractional Calculus and Applied Analysis,
Vol. 25,
Issue. 5,
p.
1873.
Kataria, Kuldeep Kumar
and
Khandakar, Mostafizar
2022.
Time-changed space-time fractional Poisson process.
Stochastic Analysis and Applications,
Vol. 40,
Issue. 2,
p.
246.
Di Crescenzo, Antonio
and
Meoli, Alessandra
2023.
Competing risks and shock models governed by a generalized bivariate Poisson process.
Journal of Applied Probability,
Vol. 60,
Issue. 2,
p.
709.
Maheshwari, Aditya
2023.
Tempered space fractional negative binomial process.
Statistics & Probability Letters,
Vol. 196,
Issue. ,
p.
109799.
Yakubovich, Yu. V.
and
Rusakov, O. V.
2023.
On Spectral Properties of Stationary Random Processes Connected by a Special Random Time Change.
Journal of Mathematical Sciences,
Vol. 273,
Issue. 5,
p.
871.
Gupta, Neha
and
Kumar, Arun
2023.
Fractional Poisson Processes of Order k and Beyond.
Journal of Theoretical Probability,
Vol. 36,
Issue. 4,
p.
2165.
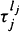 of jumps with height lj (
of jumps with height lj (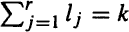 ) under the condition N(t) = k for all these special processes is investigated in detail.
) under the condition N(t) = k for all these special processes is investigated in detail.
