Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-28T20:05:12.172Z Has data issue: false hasContentIssue false
  • English
  • Français

A Markov jump process associated with the matrix-exponential distribution

Part of: Markov processes Special processes Distribution theory - Probability

Published online by Cambridge University Press:  20 September 2022

Oscar Peralta Open the ORCID record for Oscar Peralta [Opens in a new window]
Oscar Peralta*
Affiliation:
University of Lausanne and the University of Adelaide
*
*Postal address: University of Lausanne, Faculty of Business and Economics, Quartier de Chambronne, 1015 Lausanne, Switzerland. Email address: oscar.peraltagutierrez@unil.ch
Get access Rights & Permissions [Opens in a new window]

Abstract

Let f be the density function associated to a matrix-exponential distribution of parameters 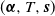$(\boldsymbol{\alpha}, T,\boldsymbol{{s}})$ . By exponentially tilting f, we find a probabilistic interpretation which generalizes the one associated to phase-type distributions. More specifically, we show that for any sufficiently large 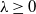$\lambda\ge 0$ , the function 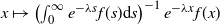$x\mapsto \left(\int_0^\infty e^{-\lambda s}f(s)\textrm{d} s\right)^{-1}e^{-\lambda x}f(x)$ can be described in terms of a finite-state Markov jump process whose generator is tied to T. Finally, we show how to revert the exponential tilting in order to assign a probabilistic interpretation to f itself.

Keywords

Phase-type distributionmatrix-analytic methodsexponential tiltingfinite-state Markov jump process

MSC classification

Primary: 60J27: Continuous-time Markov processes on discrete state spaces
Secondary: 60E05: Distributions 60K25: Queueing theory
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 1 , March 2023 , pp. 1 - 13
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmussen, S. and Bladt, M. (1996). Renewal theory and queueing algorithms for matrix-exponential distributions. In Matrix-Analytic Methods in Stochastic Models, CRC Press, Boca Raton, pp. 313–341.Google Scholar
Asmussen, S. and Bladt, M. (1999). Point processes with finite-dimensional conditional probabilities. Stoch. Process. Appl. 82, 127–142.CrossRefGoogle Scholar
Bean, N. G., Nguyen, G. T., Nielsen, B. F. and Peralta, O. (2022). RAP-modulated fluid processes: first passages and the stationary distribution. Stoch. Process. Appl. 149, 308–340.Google Scholar
Bean, N. G. and Nielsen, B. F. (2010). Quasi-birth-and-death processes with rational arrival process components. Stoch. Models 26, 309–334.CrossRefGoogle Scholar
Bladt, M. and Neuts, M. F. (2003). Matrix-exponential distributions: calculus and interpretations via flows. Stoch. Models 19, 113–124.CrossRefGoogle Scholar
Bladt, M. and Nielsen, B. F. (2017). Matrix-Exponential Distributions in Applied Probability. Springer, New York.CrossRefGoogle Scholar
Commault, C. and Mocanu, S. (2003). Phase-type distributions and representations: some results and open problems for system theory. Internat. J. Control 76, 566–580.CrossRefGoogle Scholar
Cox, D. R. (1955). A use of complex probabilities in the theory of stochastic processes. Math. Proc. Camb. Phil. Soc. 51, 313–319.CrossRefGoogle Scholar
Cox, D. R. (1955). The analysis of non-Markovian stochastic processes by the inclusion of supplementary variables. Math. Proc. Camb. Phil. Soc. 51, 433–441.CrossRefGoogle Scholar
Cramér, H. (2013). Collective risk theory: a survey of the theory from the point of view of the theory of stochastic processes. In Collected Works II, Springer, Berlin, Heidelberg, pp. 1028–1115.Google Scholar
Escher, F. (1932). On the probability function in the collective theory of risk. Scand. Actuarial J. 15, 175–195.Google Scholar
Farina, L. and Rinaldi, S. (2000). Positive Linear Systems: Theory and Applications. John Wiley, New York.CrossRefGoogle Scholar
Gerber, H. and Shiu, E. (1994). Option pricing by Esscher transforms. Trans. Soc. Actuaries 46, 99–140.Google Scholar
Jensen, A. (1954). A Distribution Model Applicable to Economics. Munksgaard, Copenhagen.Google Scholar
Neuts, M. (1975). Probability distributions of phase type. In Liber Amicorum Prof. Emeritus H. Florin, Department of Mathematics, University of Louvain, pp. 173–206.Google Scholar
Neuts, M. (1981). Matrix-Geometric Solutions in Stochastic Models: an Algorithmic Approach. Johns Hopkins University Press, Baltimore.Google Scholar
O’Cinneide, C. A. (1990). Characterization of phase-type distributions. Stoch. Models 6, 1–57.CrossRefGoogle Scholar
Völlering, F. (2020). Markov process representation of semigroups whose generators include negative rates. Electron. Commun. Prob. 25, 7 pp.CrossRefGoogle Scholar