Hostname: page-component-89b8bd64d-shngb Total loading time: 0 Render date: 2026-05-06T06:53:31.774Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-reversible guided Metropolis kernel

Part of: Markov processes Probabilistic methods, simulation and stochastic differential equations

Published online by Cambridge University Press:  12 April 2023

Kengo Kamatani Open the ORCID record for Kengo Kamatani [Opens in a new window]  and
Xiaolin Song
Kengo Kamatani*
Affiliation:
The Institute of Statistical Mathematics
Xiaolin Song*
Affiliation:
Osaka University
*
*Postal address: 10-3 Midori-cho, Tachikawa Tokyo 190-8562, Japan. Email address: kamatani@ism.ac.jp
**Postal address: Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama-cho, Toyonaka, Osaka, Japan. Email address: songxl@sigmath.es.osaka-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a class of non-reversible Metropolis kernels as a multivariate extension of the guided-walk kernel proposed by Gustafson (Statist. Comput. 8, 1998). The main idea of our method is to introduce a projection that maps a state space to a totally ordered group. By using Haar measure, we construct a novel Markov kernel termed the Haar mixture kernel, which is of interest in its own right. This is achieved by inducing a topological structure to the totally ordered group. Our proposed method, the 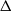$\Delta$-guided Metropolis–Haar kernel, is constructed by using the Haar mixture kernel as a proposal kernel. The proposed non-reversible kernel is at least 10 times better than the random-walk Metropolis kernel and Hamiltonian Monte Carlo kernel for the logistic regression and a discretely observed stochastic process in terms of effective sample size per second.

Keywords

Markov chain Monte CarloreversibilityHaar measureBayesian inference

MSC classification

Primary: 65C05: Monte Carlo methods 65C40: Computational Markov chains
Secondary: 60J05: Discrete-time Markov processes on general state spaces

Information

Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 3 , September 2023 , pp. 955 - 981
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andrieu, C. (2016). On random- and systematic-scan samplers. Biometrika 103, 719–726.CrossRefGoogle Scholar
Andrieu, C. and Livingstone, S. (2021). Peskun–Tierney ordering for Markovian Monte Carlo: beyond the reversible scenario. Ann. Statist. 49, 1958–1981.CrossRefGoogle Scholar
Berger, J. O. (1993). Statistical Decision Theory and Bayesian Analysis. Springer, New York.Google Scholar
Beskos, A. et al. (2017). Geometric MCMC for infinite-dimensional inverse problems. J. Comput. Phys. 335, 327–351.CrossRefGoogle Scholar
Beskos, A., Papaspiliopoulos, O. and Roberts, G. (2009). Monte Carlo maximum likelihood estimation for discretely observed diffusion processes. Ann. Statist. 37, 223–245.CrossRefGoogle Scholar
Beskos, A., Papaspiliopoulos, O., Roberts, G. O. and Fearnhead, P. (2006). Exact and computationally efficient likelihood-based estimation for discretely observed diffusion processes (with discussion). J. R. Statist. Soc. B [Statist. Methodology] 68, 333–382.CrossRefGoogle Scholar
Beskos, A., Pillai, N., Roberts, G., Sanz-Serna, J.-M. and Stuart, A. (2013). Optimal tuning of the hybrid Monte Carlo algorithm. Bernoulli 19, 1501–1534.CrossRefGoogle Scholar
Beskos, A., Roberts, G., Stuart, A. and Voss, J. (2008). MCMC methods for diffusion bridges. Stoch. Dynamics 8, 319–350.CrossRefGoogle Scholar
Bierkens, J. (2016). Non-reversible Metropolis–Hastings. Statist. Comput. 26, 1213–1228.CrossRefGoogle Scholar
Bierkens, J., Fearnhead, P. and Roberts, G. (2019). The zig-zag process and super-efficient sampling for Bayesian analysis of big data. Ann. Statist. 47, 1288–1320.CrossRefGoogle Scholar
Bouchard-Côté, A., Vollmer, S. J. and Doucet, A. (2018). The bouncy particle sampler: a nonreversible rejection-free Markov chain Monte Carlo method. J. Amer. Statist. Assoc. 113, 855–867.CrossRefGoogle Scholar
Chopin, N. and Ridgway, J. (2017). Leave Pima Indians alone: binary regression as a benchmark for Bayesian computation. Statist. Sci. 32, 64–87.CrossRefGoogle Scholar
Cotter, S. L., Roberts, G. O., Stuart, A. M. and White, D. (2013). MCMC methods for functions: modifying old algorithms to make them faster. Statist. Sci. 28, 424–446.CrossRefGoogle Scholar
Diaconis, P., Holmes, S. and Neal, R. M. (2000). Analysis of a nonreversible Markov chain sampler. Ann. Appl. Prob. 10, 726–752.CrossRefGoogle Scholar
Diaconis, P. and Saloff-Coste, L. (1993). Comparison theorems for reversible Markov chains. Ann. Appl. Prob. 3, 696.CrossRefGoogle Scholar
Dua, D. and Graff, C. (2017). UCI Machine Learning Repository. Available at https://archive.ics.uci.edu/ml/index.php. University of California, Irvine, School of Information and Computer Science.Google Scholar
Duane, S., Kennedy, A., Pendleton, B. J. and Roweth, D. (1987). Hybrid Monte Carlo. Phys. Lett. B 195, 216–222.CrossRefGoogle Scholar
Eddelbuettel, D. and Sanderson, C. (2014). RcppArmadillo: accelerating R with high-performance C++ linear algebra. Comput. Statist. Data Anal. 71, 1054–1063.CrossRefGoogle Scholar
Florens-zmirou, D. (1989). Approximate discrete-time schemes for statistics of diffusion processes. Statistics 20, 547–557.CrossRefGoogle Scholar
Gagnon, P. and Maire, F. (2020). Lifted samplers for partially ordered discrete state-spaces. Preprint. Available at https://arxiv.org/abs/2003.05492v1.Google Scholar
Ghosh, J. K., Delampady, M. and Samanta, T. (2006). An Introduction to Bayesian Analysis. Springer, New York.Google Scholar
Green, P. J., Łatuszyński, K., Pereyra, M. and Robert, C. P. (2015). Bayesian computation: a summary of the current state, and samples backwards and forwards. Statist. Comput. 25, 835–862.CrossRefGoogle Scholar
Gustafson, P. (1998). A guided walk Metropolis algorithm. Statist. Comput. 8, 357–364.CrossRefGoogle Scholar
Halmos, P. R. (1950). Measure Theory. D. Van Nostrand, New York.CrossRefGoogle Scholar
Hobert, J. P. and Marchev, D. (2008). A theoretical comparison of the data augmentation, marginal augmentation and PX-DA algorithms. Ann. Statist. 36, 532–554.CrossRefGoogle Scholar
Horowitz, A. M. (1991). A generalized guided Monte Carlo algorithm. Phys. Lett. B 268, 247–252.CrossRefGoogle Scholar
Hosseini, B. (2019). Two Metropolis–Hastings algorithms for posterior measures with non-Gaussian priors in infinite dimensions. SIAM/ASA J. Uncertainty Quantif. 7, 1185–1223.CrossRefGoogle Scholar
Kamatani, K. (2017). Ergodicity of Markov chain Monte Carlo with reversible proposal. J. Appl. Prob. 54, 638–654.CrossRefGoogle Scholar
Kamatani, K. (2018). Efficient strategy for the Markov chain Monte Carlo in high-dimension with heavy-tailed target probability distribution. Bernoulli 24, 3711–3750.CrossRefGoogle Scholar
Kipnis, C. and Varadhan, S. R. S. (1986). Central limit theorem for additive functionals of reversible Markov processes and applications to simple exclusions. Commun. Math. Phys. 104, 1–19.CrossRefGoogle Scholar
Kontoyiannis, I. and Meyn, S. P. (2011). Geometric ergodicity and the spectral gap of non-reversible Markov chains. Prob. Theory Relat. Fields 154, 327–339.CrossRefGoogle Scholar
Kotz, S. and Nadarajah, S. (2004). Multivariate t Distributions and Their Applications. Cambridge University Press.CrossRefGoogle Scholar
Lewis, P. A. W., McKenzie, E. and Hugus, D. K. (1989). Gamma processes. Commun. Statist. Stoch. Models 5, 1–30.CrossRefGoogle Scholar
Liu, J. S. and Sabatti, C. (2000). Generalised Gibbs sampler and multigrid Monte Carlo for Bayesian computation. Biometrika 87, 353–369.CrossRefGoogle Scholar
Liu, J. S. and Wu, Y. N. (1999). Parameter expansion for data augmentation. J. Amer. Statist. Assoc. 94, 1264–1274.CrossRefGoogle Scholar
Ludkin, M. and Sherlock, C. (2022). Hug and hop: a discrete-time, nonreversible Markov chain Monte Carlo algorithm. To appear in Biometrika.Google Scholar
Ma, Y.-A., Chen, T. and Fox, E. B. (2015). A complete recipe for stochastic gradient MCMC. In Proc. 28th International Conference on Neural Information Processing Systems (NIPS ’15), Vol. 2, MIT Press, pp. 2917–2925.Google Scholar
Ma, Y.-A., Fox, E. B., Chen, T. and Wu, L. (2019). Irreversible samplers from jump and continuous Markov processes. Statist. Comput. 29, 177–202.CrossRefGoogle Scholar
Neal, R. M. (1999). Regression and classification using Gaussian process priors. In Bayesian Statistics 6, Oxford University Press, New York, pp. 475–501.Google Scholar
Neal, R. M. (2011). MCMC using Hamiltonian dynamics. In Handbook of Markov Chain Monte Carlo, CRC Press, Boca Raton, FL, pp. 113–162.Google Scholar
Neal, R. M. (2020). Non-reversibly updating a uniform [0,1] value for Metropolis accept/reject decisions. Preprint. Available at https://arxiv.org/abs/2001.11950.Google Scholar
Neiswanger, W., Wang, C. and Xing, E. P. (2014). Asymptotically exact, embarrassingly parallel MCMC. In Proc. Thirtieth Conference on Uncertainty in Artificial Intelligence (UAI ’14), AUAI Press, Arlington, VA, pp. 623–632.Google Scholar
Ottobre, M., Pillai, N. S., Pinski, F. J. and Stuart, A. M. (2016). A function space HMC algorithm with second order Langevin diffusion limit. Bernoulli 22, 60–106.CrossRefGoogle Scholar
Plummer, M., Best, N., Cowles, K. and Vines, K. (2006). CODA: convergence diagnosis and output analysis for MCMC. R News 6, 7–11.Google Scholar
Prakasa Rao, B. L. S. (1983). Asymptotic theory for non-linear least squares estimator for diffusion processes. Ser. Statist. 14, 195–209.CrossRefGoogle Scholar
Prakasa Rao, B. L. S. (1988). Statistical inference from sampled data for stochastic processes. In Statistical Inference from Stochastic Processes (Ithaca, NY, 1987), American Mathematical Society, Providence, RI, pp. 249–284.CrossRefGoogle Scholar
R Core Team (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna.Google Scholar
Robert, C. and Casella, G. (2011). A short history of Markov chain Monte Carlo: subjective recollections from incomplete data. Statist. Sci. 26, 102–115.CrossRefGoogle Scholar
Robert, C. P. (2007). The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation, 2nd edn. Springer, New York.Google Scholar
Roberts, G. O. and Rosenthal, J. S. (1997). Geometric ergodicity and hybrid Markov chains. Electron. Commun. Prob. 2, 13–25.CrossRefGoogle Scholar
Roberts, G. O. and Rosenthal, J. S. (1998). Optimal scaling of discrete approximations to Langevin diffusions. J. R. Statist. Soc. B [Statist. Methodology] 60, 255–268.CrossRefGoogle Scholar
Roberts, G. O. and Tweedie, R. L. (1996). Exponential convergence of Langevin diffusions and their discrete approximations. Bernoulli 2, 341–363.CrossRefGoogle Scholar
Roberts, G. O. and Tweedie, R. L. (2001). Geometric $L^2$ and $L^1$ convergence are equivalent for reversible Markov chains. J. Appl. Prob. 38A, 37–41.Google Scholar
Rossky, P. J., Doll, J. D. and Friedman, H. L. (1978). Brownian dynamics as smart Monte Carlo simulation. J. Chem. Phys. 69, 4628–4633.CrossRefGoogle Scholar
Sato, K. (1999). Lévy Processes and Infinitely Divisible Distributions. Cambridge University Press.Google Scholar
Scott, S. L. et al. (2016). Bayes and big data: the consensus Monte Carlo algorithm. Internat. J. Manag. Sci. Eng. Manag. 11, 78–88.Google Scholar
Shariff, R., György, A. and Szepesvári, C. (2015). Exploiting symmetries to construct efficient MCMC algorithms with an application to SLAM. In Proc. Eighteenth International Conference on Artificial Intelligence and Statistics (Proc. Machine Learning Research 38), eds G. Lebanon and S. V. N. Vishwanathan, PMLR, San Diego, CA, pp. 866–874.Google Scholar
Sherlock, C. and Thiery, A. H. (2022). A discrete bouncy particle sampler. Biometrika 109, 335–349.CrossRefGoogle Scholar
Stan Development Team (2020). RStan: the R interface to Stan. R package version 2.21.2. Available at http://mc-stan.org.Google Scholar
Titsias, M. K. and Papaspiliopoulos, O. (2018). Auxiliary gradient-based sampling algorithms. J. R. Statist. Soc. B [Statist. Methodology] 80, 749–767.CrossRefGoogle Scholar
Tripuraneni, N., Rowland, M., Ghahramani, Z. and Turner, R. (2017). Magnetic Hamiltonian Monte Carlo. In Proc. 34th International Conference on Machine Learning (Proc. Machine Learning Research 70), eds D. Precup and Y. W. Teh, PMLR, Sydney, pp. 3453–3461.Google Scholar
Turitsyn, K. S., Chertkov, M. and Vucelja, M. (2011). Irreversible Monte Carlo algorithms for efficient sampling. Physica D 240, 410–414.CrossRefGoogle Scholar
Vucelja, M. (2016). Lifting—a nonreversible Markov chain Monte Carlo algorithm. Amer. J. Phys. 84, 958–968.CrossRefGoogle Scholar
Wang, X. and Dunson, D. B. (2013). Parallelizing MCMC via Weierstrass sampler. Preprint. Available at https://arxiv.org/abs/1312.4605.Google Scholar
Welling, M. and Teh, Y. W. (2011). Bayesian learning via stochastic gradient Langevin dynamics. In Proc. 28th International Conference on Machine Learning (ICML ’11), Omnipress, Madison, WI, pp. 681–688.Google Scholar
Yoshida, N. (1992). Estimation for diffusion processes from discrete observation. J. Multivariate Anal. 41, 220–242.CrossRefGoogle Scholar