Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-18T06:45:04.424Z Has data issue: false hasContentIssue false
  • English
  • Français

Notes on random chords in convex bodies

Part of: Geometric probability and stochastic geometry

Published online by Cambridge University Press:  14 July 2016

E. G. Enns  and
P. F. Ehlers
E. G. Enns
Affiliation:
University of Calgary
P. F. Ehlers*
Affiliation:
University of Calgary
*
∗ Postal address for both authors: Department of Mathematics, University of Calgary, 2500 University Drive N.W., Calgary, Alberta, Canada T2N 1N4.
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a compact body E embedded in a convex compact body G. A point P is randomly chosen in E and three different rays to the boundary ∂G of G are generated by P. Ray 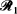is in a uniformly random direction and has length R, ray 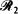is through a second random point chosen from within G and has length W, and ray 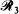is to a random point in ∂G and has length Y. The distribution of Y is obtained and is related to previous work. When E is specialized to G or to ∂G, other known results are retrieved. The paper ends with a discussion of a conjecture relating the means of R, W and Y.

Keywords

GEOMETRIC PROBABILITYRAYSCHORDSCONVEXITY

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Type
Research Papers
Information
Journal of Applied Probability , Volume 30 , Issue 4 , December 1993 , pp. 889 - 897
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors acknowledge the support of the National Science and Engineering Research Council of Canada. Part of this work was completed at the Australian National University.

References

Coleman, R. (1989) Random sections of a sphere. Canad. J. Statist. 17, 27–39.CrossRefGoogle Scholar
Ehlers, P. F. and Enns, E. G. (1981) Random secants of a convex body generated by surface randomness. J. Appl. Prob. 18, 157–166.Google Scholar
Enns, E. G. and Ehlers, P. F. (1980) Random paths originating within a convex region and terminating on its surface. Austral. J. Statist. 22, 60–68.Google Scholar
Enns, E. G. and Ehlers, P. F. (1988) Chords through a convex body generated from within an embedded body. J. Appl. Prob. 25, 700–707.CrossRefGoogle Scholar
Hadwiger, H. (1955) Altes und Neues über konvexe Körper. Birkhäuser, Basel.Google Scholar
Kellerer, A. M. (1984) Chord-length distributions and related quantities for spheroids. Radiation Res. 98, 425–437.Google Scholar
Kingman, J. F. C. (1969) Random secants of a convex body. J. Appl. Prob. 6, 660–672.CrossRefGoogle Scholar
Miles, R. E. (1969) Poisson flats in Euclidean spaces. Part I: A finite number of random uniform flats. Adv. Appl. Prob. 1, 211–237.CrossRefGoogle Scholar
Miles, R. E. (1980) The random tangential projection of a surface. Adv. Appl. Prob. 12, 425–446.Google Scholar
Miles, R. E. and Davy, P. (1976) Precise and general conditions for the validity of a comprehensive set of stereological fundamental formulae. J. Microsc. 107, 211–236.Google Scholar
Ruben, H. and Reed, W. J. (1980) A more general form of a theorem of Crofton. J. Appl. Prob. 10, 479–482.Google Scholar
Santaló, L. A. (1976) Integral Geometry and Geometric Probability. Vol. 1 of Encyclopedia of Mathematics and its Applications. Addison-Wesley, Reading, MA.Google Scholar
Saxl, I. and Rataj, J. (1989) Random paths in non-convex bodies. In Geobild '89: Mathematical Research, ed. Hübler, A. et al. 51, pp. 93–98. Akademie Verlag, Berlin.Google Scholar
Sheng, T. K. (1985) The distance between two random points in plane regions. Adv. Appl. Prob. 17, 748–773.Google Scholar