No CrossRef data available.
Article contents
Reciprocal properties of random fields on undirected graphs
Published online by Cambridge University Press: 31 January 2023
Abstract
We clarify and refine the definition of a reciprocal random field on an undirected graph, with the reciprocal chain as a special case, by introducing four new properties: the factorizing, global, local, and pairwise reciprocal properties, in decreasing order of strength, with respect to a set of nodes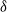 
$\delta$. They reduce to the better-known Markov properties if 
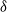$\delta$ is the empty set, or, with the exception of the local property, if 
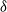$\delta$ is a complete set. Conditions for each reciprocal property to imply the next stronger property are derived, and it is shown that, conditionally on the values at a set of nodes 
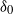$\delta_0$, all four properties are preserved for the subgraph induced by the remaining nodes, with respect to the node set 
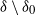$\delta\setminus\delta_0$. We note that many of the above results are new even for reciprocal chains.
Keywords
MSC classification
Primary:
60G60: Random fields
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
Bernstein, S. (1932). Sur les liaisons entre les grandeurs aléatoires. In: Verh. des Intern. Mathematikerkongr. Vol. 1, Zürich.Google Scholar
Carmichael, J. P., Masse, J. C. and Theodorescu, R. (1982). Processus Gaussiens stationaires réciproques sur un intervalle. C. R. Acad. Sci. Paris Sér. I Math. 295, 291–293.Google Scholar
Carravetta, F. (2008). Nearest-neighbour modelling of reciprocal chains. Stochastics 80, 525–584.CrossRefGoogle Scholar
Chay, S. C. (1972). On quasi-Markov random fields. J. Multivar. Anal. 2, 14–76.10.1016/0047-259X(72)90010-3CrossRefGoogle Scholar
Csiszár, I. (1975).
I-divergence geometry of probability distributions and minimization problems. Ann. Prob. 3, 146–158.CrossRefGoogle Scholar
Darroch, J. N., Lauritzen, S. L. and Speed, T. P. (1980). Markov fields and log-linear models for contingency tables. Ann. Statist. 8, 522–539.10.1214/aos/1176345006CrossRefGoogle Scholar
Dobrushin, R. L. (1968). Description of a random field by means of its conditional probabilities and conditions of its regularity. Theory Prob. Appl. 13, 197–224.10.1137/1113026CrossRefGoogle Scholar
Dobrushin, R. L. (1970). Prescribing a system of random variables by conditional distributions. Theory Prob. Appl. 15, 458–486.10.1137/1115049CrossRefGoogle Scholar
Erhardsson, T., Saize, S. and Yang, X. (2020). Reciprocal chains: Foundations. IEEE Trans. Automatic Control 65, 4840–4845.10.1109/TAC.2019.2958834CrossRefGoogle Scholar
Föllmer, H. (1988). Random fields and diffusion processes. In: École d’été de Probabilités de Saint-Flour XV-XVII-1985-87 (Lect. Notes Math. 1362). Springer, Berlin.Google Scholar
Jamison, B. (1970). Reciprocal processes: The stationary Gaussian case. Ann. Math. Statist. 41, 1624–1630.CrossRefGoogle Scholar
Jamison, B. (1974). Reciprocal processes. Z. Wahrscheinlichkeitsth. 30, 65–86.CrossRefGoogle Scholar
Kindermann, R. and Snell, J. L. (1980). Markov Random Fields and their Applications (Contemporary Math. 1). American Mathematical Society, Providence, RI.Google Scholar
Krener, A. J. (1988). Reciprocal diffusions and stochastic differential equations of second order. Stochastics 24, 393–422.CrossRefGoogle Scholar
Lauritzen, S. L. (1996). Graphical Models (Oxford Statist. Sci. Ser. 17). Clarendon Press, Oxford.Google Scholar
Léonard, C., Rœlly, S. and Zambrini, J.-C. (2014). Reciprocal processes. A measure-theoretical point of view. Prob. Surv. 11, 237–269.CrossRefGoogle Scholar
Levy, B. C., Frezza, R. and Krener, A. J. (1990). Modeling and estimation of discrete-time Gaussian reciprocal processes. IEEE Trans. Automatic Control 35, 1013–1023.10.1109/9.58529CrossRefGoogle Scholar
Matúš, F. (1992). On equivalence of Markov properties over undirected graphs. J. Appl. Prob. 29, 745–749.CrossRefGoogle Scholar
Moussouris, J. (1974). Gibbs and Markov random systems with constraints. J. Statist. Phys. 10, 11–33.CrossRefGoogle Scholar
Pearl, J. (1988). Probabilistic Reasoning in Intelligent Systems. Morgan Kaufmann, San Mateo, CA.Google Scholar
Picci, G. and Carli, F. P. (2008). Modelling and simulation of images by reciprocal processes. In: Proc. Tenth Int. Conf. Computer Modeling and Simulation. UKSIM 2008, 513–518.Google Scholar
Preston, C. J. (1974). Gibbs States on Countable Sets (Cambridge Tracts Math. 68). Cambridge University Press.Google Scholar
Sand, J.-Å. (1996). Reciprocal realizations on the circle. SIAM J. Control Optim. 34, 507–520.CrossRefGoogle Scholar
Schrödinger, E. (1931). Über die Umkehrung der Naturgesetze. Sitzungsberichte Preuss. Akad. Wiss. Berlin. Phys. Math. 144, 144–153.Google Scholar
Speed, T. P. (1979). A note on nearest-neighbour Gibbs and Markov probabilities. Sankhyā A 41, 184–197.Google Scholar
Spitzer, F. (1971). Markov random fields and Gibbs ensembles. Ann. Math. Monthly 78, 142–154.CrossRefGoogle Scholar
Stamatescu, G., White, L. B. and Bruce-Doust, R. (2018). Track extraction with hidden reciprocal chains. IEEE Trans. Automatic Control 63, 1097–1104.CrossRefGoogle Scholar
Studený, M. (1989). Multiinformation and the problem of characterization of conditional independence relations. Problems Control Inform. Theory 18, 3–16.Google Scholar
White, L. B. and Carravetta, A. (2011). Optimal smoothing for finite state hidden reciprocal processes. IEEE Trans. Automatic Control 56, 2156–2161.10.1109/TAC.2011.2141510CrossRefGoogle Scholar
Whittaker, J. (1990). Graphical Models in Applied Multivariate Statistics. John Wiley, Chichester.Google Scholar