Published online by Cambridge University Press: 07 February 2022
Consider two-type linear-fractional branching processes in varying environments with asymptotically constant mean matrices. Let  $\nu$
be the extinction time. Under certain conditions, we show that both
$\nu$
be the extinction time. Under certain conditions, we show that both 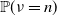 $\mathbb{P}(\nu=n)$
and
$\mathbb{P}(\nu=n)$
and 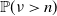 $\mathbb{P}(\nu>n)$
are asymptotically the same as some functions of the products of spectral radii of the mean matrices. We also give an example for which
$\mathbb{P}(\nu>n)$
are asymptotically the same as some functions of the products of spectral radii of the mean matrices. We also give an example for which 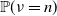 $\mathbb{P}(\nu=n)$
decays with various speeds such as
$\mathbb{P}(\nu=n)$
decays with various speeds such as 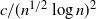 ${c}/({n^{1/2}\log n)^2}$
,
${c}/({n^{1/2}\log n)^2}$
, 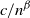 ${c}/{n^\beta}$
,
${c}/{n^\beta}$
, 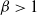 $\beta >1$
, which are very different from those of homogeneous multitype Galton–Watson processes.
$\beta >1$
, which are very different from those of homogeneous multitype Galton–Watson processes.