Article contents
About bubbles and vortex rings
Published online by Cambridge University Press: 02 September 2015
Abstract
Bubble interaction with turbulence has a number of applications in engineering processes and nature. The complex interplay between the vortical structures present in a turbulent flow and the bubbles drives their deformation dynamics, which may lead to bubble rupture under the appropriate conditions. Such a process includes nonlinear interaction among the turbulent eddies and between the eddies and the bubbles. Thus, the coupled evolution of a single vortex ring with a bubble represents an idealized scenario that can provide a framework to shed light on understanding such a common and complex mechanism. Jha & Govardhan (J. Fluid Mech., vol. 773, 2015, pp. 460–497) have performed elegant experiments generating controlled vortex rings and injecting bubbles of known volume. They have reported interesting results on the elongation process of the bubble and its impact on vortex dynamics.
Information
- Type
- Focus on Fluids
- Information
- Copyright
- © 2015 Cambridge University Press
References
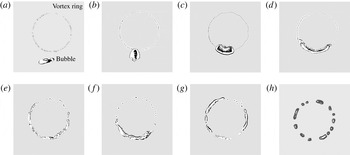
Figure 1. Time sequence of the interaction of a vortex ring with a bubble taken from Jha & Govardhan (2015). Here the bubble $\mathit{We}=4.8$,
$R/a=4$,
$R/R_{b}=3.8$ and
$a/R_{b}=0.96$.

Figure 2. Three-dimensional numerical simulations of bubbles interacting with a vortex ring at two supercritical Weber numbers as performed by Revuelta (2010): (a) $\mathit{We}=2$, (b)
$\mathit{We}=5$. In the simulations
$\mathit{Re}=1000$,
$R/R_{b}=1.5$ and
$a/R_{b}=0.05$.



1. Introduction
Two-phase turbulent flows are common in many industrial applications and natural processes. In the case of bubbly flows, the interaction of turbulent eddies with bubbles determines the resulting bubble size distribution present in the turbulent flow. The bubble breakup problem has been widely investigated since the seminal works of Kolmogorov (Reference Kolmogorov1949) and Hinze (Reference Hinze1955), and two different bubble breakup mechanisms are well established depending on the Weber number, $We={\it\rho}{\it\varepsilon}^{2/3}R_{b}^{5/3}/{\it\sigma}$
, defined as the ratio between the turbulent stresses acting on the surface of the bubble,
$We={\it\rho}{\it\varepsilon}^{2/3}R_{b}^{5/3}/{\it\sigma}$
, defined as the ratio between the turbulent stresses acting on the surface of the bubble,
 ${\it\tau}_{t}\sim {\it\rho}({\it\varepsilon}R_{b})^{2/3}$
, and the confining stresses due to surface tension,
${\it\tau}_{t}\sim {\it\rho}({\it\varepsilon}R_{b})^{2/3}$
, and the confining stresses due to surface tension,
 ${\it\tau}_{s}\sim {\it\sigma}/R_{b}$
. The first mechanism, occurring at high Weber numbers, is an inertial mechanism leading to bubble breakup, produced when the pressure fluctuations acting on the bubble surface are sufficiently large to overcome the confining surface tension forces (Martínez-Bazán et al.
Reference Martínez-Bazán, Montañes and Lasheras1999). The second, at low Weber numbers, is a resonance mechanism between the oscillation of the bubble and the turbulent flow. This mechanism leads to an accumulation of surface energy due to the bubble interaction with a sequence of turbulent eddies until the bubble breaks (Risso & Fabre Reference Risso and Fabre1998; Lauterborn & Kurz Reference Lauterborn and Kurz2010). Thus, at supercritical Weber numbers,
${\it\tau}_{s}\sim {\it\sigma}/R_{b}$
. The first mechanism, occurring at high Weber numbers, is an inertial mechanism leading to bubble breakup, produced when the pressure fluctuations acting on the bubble surface are sufficiently large to overcome the confining surface tension forces (Martínez-Bazán et al.
Reference Martínez-Bazán, Montañes and Lasheras1999). The second, at low Weber numbers, is a resonance mechanism between the oscillation of the bubble and the turbulent flow. This mechanism leads to an accumulation of surface energy due to the bubble interaction with a sequence of turbulent eddies until the bubble breaks (Risso & Fabre Reference Risso and Fabre1998; Lauterborn & Kurz Reference Lauterborn and Kurz2010). Thus, at supercritical Weber numbers,
 $\mathit{We}>\mathit{We}_{c}$
, the bubble will break due to the inertial mechanism in a time
$\mathit{We}>\mathit{We}_{c}$
, the bubble will break due to the inertial mechanism in a time
 $t_{b}$
that depends on its Reynolds and Weber numbers. Otherwise, at subcritical Weber numbers,
$t_{b}$
that depends on its Reynolds and Weber numbers. Otherwise, at subcritical Weber numbers,
 $\mathit{We}<\mathit{We}_{c}$
, the bubble will remain unbroken or it might break at much longer times due to the resonance mechanism. Besides the interest in modelling the turbulent bubble breakup process, another important aspect of the bubble dynamics and deformation is its relevance in drag reduction applications due to their interaction with the turbulent structures of the flow (see van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013).
$\mathit{We}<\mathit{We}_{c}$
, the bubble will remain unbroken or it might break at much longer times due to the resonance mechanism. Besides the interest in modelling the turbulent bubble breakup process, another important aspect of the bubble dynamics and deformation is its relevance in drag reduction applications due to their interaction with the turbulent structures of the flow (see van Gils et al.
Reference van Gils, Narezo Guzman, Sun and Lohse2013).
Figure 1. Time sequence of the interaction of a vortex ring with a bubble taken from Jha & Govardhan (Reference Jha and Govardhan2015). Here the bubble $\mathit{We}=4.8$
,
$\mathit{We}=4.8$
,
 $R/a=4$
,
$R/a=4$
,
 $R/R_{b}=3.8$
and
$R/R_{b}=3.8$
and
 $a/R_{b}=0.96$
.
$a/R_{b}=0.96$
.
A simplified model to describe the interaction of bubbles with the turbulent eddies consists of a bubble of radius $R_{b}$
interacting with a single vortex ring, thus modelling a turbulent eddy by a vortex ring of circulation
$R_{b}$
interacting with a single vortex ring, thus modelling a turbulent eddy by a vortex ring of circulation
 ${\it\Gamma}$
, radius
${\it\Gamma}$
, radius
 $R$
and core size
$R$
and core size
 $a$
. In this case, the characteristic vortex velocity is given by
$a$
. In this case, the characteristic vortex velocity is given by
 $U_{c}={\it\Gamma}/(2{\rm\pi}R)$
and the problem can be analysed in terms of the bubble Reynolds number
$U_{c}={\it\Gamma}/(2{\rm\pi}R)$
and the problem can be analysed in terms of the bubble Reynolds number
 $\mathit{Re}={\it\Gamma}R_{b}/(2{\rm\pi}R{\it\nu})$
, the Weber number
$\mathit{Re}={\it\Gamma}R_{b}/(2{\rm\pi}R{\it\nu})$
, the Weber number
 $\mathit{We}={\it\rho}({\it\Gamma}/2{\rm\pi}R)^{2}/({\it\sigma}/R_{b})$
, the vortex-to-bubble radius ratio
$\mathit{We}={\it\rho}({\it\Gamma}/2{\rm\pi}R)^{2}/({\it\sigma}/R_{b})$
, the vortex-to-bubble radius ratio
 $R/R_{b}$
and the core-to-bubble radius ratio
$R/R_{b}$
and the core-to-bubble radius ratio
 $a/R_{b}$
. Jha & Govardhan (Reference Jha and Govardhan2015) have performed an experimental study of the interaction of bubbles with a vortex ring covering a range of Weber numbers between 0.155 and 19 according to the definition given above (or between 3 and 406 according to their definition as
$a/R_{b}$
. Jha & Govardhan (Reference Jha and Govardhan2015) have performed an experimental study of the interaction of bubbles with a vortex ring covering a range of Weber numbers between 0.155 and 19 according to the definition given above (or between 3 and 406 according to their definition as
 $\mathit{We}=0.87{\it\rho}({\it\Gamma}/2{\rm\pi}a)^{2}/({\it\sigma}/D_{b})$
with
$\mathit{We}=0.87{\it\rho}({\it\Gamma}/2{\rm\pi}a)^{2}/({\it\sigma}/D_{b})$
with
 $D_{b}=2R_{b}$
), and for vortex rings considerably larger than the bubble,
$D_{b}=2R_{b}$
), and for vortex rings considerably larger than the bubble,
 $R\geqslant R_{b}$
, whose core size is of the order of that of the bubble,
$R\geqslant R_{b}$
, whose core size is of the order of that of the bubble,
 $a\sim R_{b}$
.
$a\sim R_{b}$
.
2. Overview
Jha & Govardhan (Reference Jha and Govardhan2015) report a series of experimental results of bubbles interacting with single vortex rings, considering two different scenarios: (i) thin vortex rings with dimensionless vortex core $a/R=0.25$
and (ii) thick vortex rings with
$a/R=0.25$
and (ii) thick vortex rings with
 $a/R=0.75$
. Figure 1, taken from Jha & Govardhan (Reference Jha and Govardhan2015), shows the interaction of a bubble of size
$a/R=0.75$
. Figure 1, taken from Jha & Govardhan (Reference Jha and Govardhan2015), shows the interaction of a bubble of size
 $R_{b}\approx 3~\text{mm}$
with a vortex ring of radius
$R_{b}\approx 3~\text{mm}$
with a vortex ring of radius
 $R\approx 11.5~\text{mm}$
, core size
$R\approx 11.5~\text{mm}$
, core size
 $a\approx 2.9~\text{mm}$
and circulation
$a\approx 2.9~\text{mm}$
and circulation
 ${\it\Gamma}=245~\text{cm}^{2}~\text{s}^{-1}$
, whose Weber number is
${\it\Gamma}=245~\text{cm}^{2}~\text{s}^{-1}$
, whose Weber number is
 $\mathit{We}\approx 4.8$
. The figure shows that the bubble, which initially is outside of the vortex ring, is attracted towards the vortex due to the radial pressure gradients induced by the ring, and gets engulfed into the vortex core. Once inside the core, the bubble is elongated due to the azimuthal pressure gradients caused by its presence until it eventually breaks. This sequence is similar to the numerical results shown by Revuelta (Reference Revuelta2010, figure 11) for a case with
$\mathit{We}\approx 4.8$
. The figure shows that the bubble, which initially is outside of the vortex ring, is attracted towards the vortex due to the radial pressure gradients induced by the ring, and gets engulfed into the vortex core. Once inside the core, the bubble is elongated due to the azimuthal pressure gradients caused by its presence until it eventually breaks. This sequence is similar to the numerical results shown by Revuelta (Reference Revuelta2010, figure 11) for a case with
 $R/R_{b}=4$
and
$R/R_{b}=4$
and
 $\mathit{We}=10>\mathit{We}_{c}$
, although, in this case, the vortex core is much thinner,
$\mathit{We}=10>\mathit{We}_{c}$
, although, in this case, the vortex core is much thinner,
 $a/R_{b}=0.05$
, provoking the rupture of the bubble before being entrained inside the vortex core. However, Jha & Govardhan (Reference Jha and Govardhan2015) observed the same type of vortex–bubble interaction even at lower Weber numbers, for which bubble breakup should not take place according to Higuera (Reference Higuera2004) and Revuelta (Reference Revuelta2010). The explanation for the differences observed is the different breakup processes described. In the axisymmetric numerical simulations of Revuelta (Reference Revuelta2010), if the Weber number is large enough, the bubble adopts a lenticular shape, envelopes the vortex ring and breaks, keeping the unrealistic symmetry imposed in the process, although similar patterns are observed in the three-dimensional numerical simulations shown in figure 2. On the other hand, at subcritical Weber numbers, the vortex ring makes the bubble oscillate, inducing a flow field that pushes the vortex away from the bubble while it dissipates. Nevertheless, in the experimental work by Jha & Govardhan (Reference Jha and Govardhan2015), the bubbles are smaller than the vortex ring and, instead of wrapping the ring, they get trapped inside the core, whose size is similar to that of the bubble, and elongate azimuthally until they break. Bubble oscillations are also observed at lower Weber numbers during the elongation process.
$a/R_{b}=0.05$
, provoking the rupture of the bubble before being entrained inside the vortex core. However, Jha & Govardhan (Reference Jha and Govardhan2015) observed the same type of vortex–bubble interaction even at lower Weber numbers, for which bubble breakup should not take place according to Higuera (Reference Higuera2004) and Revuelta (Reference Revuelta2010). The explanation for the differences observed is the different breakup processes described. In the axisymmetric numerical simulations of Revuelta (Reference Revuelta2010), if the Weber number is large enough, the bubble adopts a lenticular shape, envelopes the vortex ring and breaks, keeping the unrealistic symmetry imposed in the process, although similar patterns are observed in the three-dimensional numerical simulations shown in figure 2. On the other hand, at subcritical Weber numbers, the vortex ring makes the bubble oscillate, inducing a flow field that pushes the vortex away from the bubble while it dissipates. Nevertheless, in the experimental work by Jha & Govardhan (Reference Jha and Govardhan2015), the bubbles are smaller than the vortex ring and, instead of wrapping the ring, they get trapped inside the core, whose size is similar to that of the bubble, and elongate azimuthally until they break. Bubble oscillations are also observed at lower Weber numbers during the elongation process.
Figure 2. Three-dimensional numerical simulations of bubbles interacting with a vortex ring at two supercritical Weber numbers as performed by Revuelta (Reference Revuelta2010): (a) $\mathit{We}=2$
, (b)
$\mathit{We}=2$
, (b)
 $\mathit{We}=5$
. In the simulations
$\mathit{We}=5$
. In the simulations
 $\mathit{Re}=1000$
,
$\mathit{Re}=1000$
,
 $R/R_{b}=1.5$
and
$R/R_{b}=1.5$
and
 $a/R_{b}=0.05$
.
$a/R_{b}=0.05$
.
The experiments of Jha & Govardhan (Reference Jha and Govardhan2015) can also contribute to obtaining the physical pictures underlying the effect of the bubbles on the vortical structures and the breakup time of bubbles. In fact, the authors report that, in the low-Weber-number case, the vortex core is fragmented when the bubble is trapped, with a simultaneous reduction in enstrophy and ring convection velocity. Furthermore, most phenomenological turbulent bubble breakup models inherently consider that the bubble is at the centre of the turbulent structure, although the total breakup time should include the bubble trapping time, also discussed in Jha & Govardhan (Reference Jha and Govardhan2015). However, an aspect not contemplated is the relevance of the vortex-to-bubble size ratio, $R/R_{b}$
, in the bubble breakup process.
$R/R_{b}$
, in the bubble breakup process.
3. Future
Phenomenological models for turbulent breakup of bubbles postulate that they will deform and eventually break due to their interaction with turbulent eddies whose sizes are similar to the bubble diameter. Small vortices do not have enough energy to disturb and break the bubble and large ones would transport it without breaking it up. Thus, additional experiments generating vortex rings with $R/R_{b}\sim O(1)$
and
$R/R_{b}\sim O(1)$
and
 $a/R_{b}\ll 1$
should help to elucidate their breakup efficiency and to determine if bubble breakup is caused by the flow field induced around it, as in figure 2, or by the entrainment of the bubble inside the vortex core. The results could be complemented by three-dimensional numerical simulations injecting the bubbles at different distances from the vortex ring, not only at the axis but also away from it. In addition, it is worth exploring the resonance bubble break mechanism describing the interaction of a bubble with a sequence of vortices at subcritical Weber numbers by means of experiments and numerical simulations. In this situation a vortex ring will make the bubble oscillate. On the other hand, the oscillating bubble will induce a flow field that may push away the ring. However, the interaction with other incoming vortices may increase the amplitude of the bubble oscillations, producing its rupture, as reported by Revuelta, Rodríguez-Rodríguez & Martínez-Bazán (Reference Revuelta, Rodríguez-Rodríguez and Martínez-Bazán2008) for a simplified two-dimensional model.
$a/R_{b}\ll 1$
should help to elucidate their breakup efficiency and to determine if bubble breakup is caused by the flow field induced around it, as in figure 2, or by the entrainment of the bubble inside the vortex core. The results could be complemented by three-dimensional numerical simulations injecting the bubbles at different distances from the vortex ring, not only at the axis but also away from it. In addition, it is worth exploring the resonance bubble break mechanism describing the interaction of a bubble with a sequence of vortices at subcritical Weber numbers by means of experiments and numerical simulations. In this situation a vortex ring will make the bubble oscillate. On the other hand, the oscillating bubble will induce a flow field that may push away the ring. However, the interaction with other incoming vortices may increase the amplitude of the bubble oscillations, producing its rupture, as reported by Revuelta, Rodríguez-Rodríguez & Martínez-Bazán (Reference Revuelta, Rodríguez-Rodríguez and Martínez-Bazán2008) for a simplified two-dimensional model.
Another issue to consider in future is the effect of bubbles on the characteristic properties of the vortex ring to extrapolate the results to more complex turbulent bubbly flows. Jha & Govardhan (Reference Jha and Govardhan2015) concluded that there is a dramatic decrease of enstrophy of the vortex ring after the bubbles are trapped inside the core, especially at low Weber numbers and thick vortex core cases, with a reduction in the vortex convective velocity. Such velocity reduction could be caused by vorticity redistribution inside the vortex core, although the authors argue that it is mainly produced by the development of azimuthal instabilities after bubble entrainment and vortex core fragmentation. A further investigation on this issue, combining experiments and numerical simulation, would be extremely interesting.
Acknowledgements
The author thanks Dr J. Rodríguez-Rodríguez for stimulating discussions and Dr Revuelta for providing figure 2. This work has been supported by grants nos. DPI2014-59292-C03-03-P and P11-TEP7495.