Published online by Cambridge University Press: 27 July 2017
The purpose of this paper is to characterize and model waves that are observed within the potential core of subsonic jets and relate them to previously observed tones in the near-nozzle region. The waves are detected in data from a large-eddy simulation of a Mach 0.9 isothermal jet and modelled using parallel and weakly non-parallel linear modal analysis of the Euler equations linearized about the turbulent mean flow, as well as simplified models based on a cylindrical vortex sheet and the acoustic modes of a cylindrical soft duct. In addition to the Kelvin–Helmholtz instability waves, three types of waves with negative phase velocities are identified in the potential core: upstream- and downstream-propagating duct-like acoustic modes that experience the shear layer as a pressure-release surface and are therefore radially confined to the potential core, and upstream-propagating acoustic modes that represent a weak coupling between the jet core and the free stream. The slow streamwise contraction of the potential core imposes a frequency-dependent end condition on the waves that is modelled as the turning points of a weakly non-parallel approximation of the waves. These turning points provide a mechanism by which the upstream- and downstream-travelling waves can interact and exchange energy through reflection and transmission processes. Paired with a second end condition provided by the nozzle, this leads to the possibility of resonance in limited frequency bands that are bound by two saddle points in the complex wavenumber plane. The predicted frequencies closely match the observed tones detected outside of the jet. The vortex-sheet model is then used to systematically explore the Mach number and temperature ratio dependence of the phenomenon. For isothermal jets, the model suggests that resonance is likely to occur in a narrow range of Mach number, 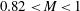 $0.82<M<1$.
$0.82<M<1$.
Present address: Center for Turbulence Research, Stanford University, Stanford, CA 94305, USA.