Article contents
Acoustic tones in the near-nozzle region of jets: characteristics and variations between Mach numbers 0.5 and 2
Published online by Cambridge University Press: 25 June 2021
Abstract
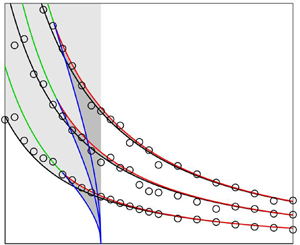
The characteristics of acoustic tones near the nozzle of jets are investigated for Mach numbers between  ${M}=0.50$ and 2 using large-eddy simulations. Peaks are observed in all cases. They are tonal for
${M}=0.50$ and 2 using large-eddy simulations. Peaks are observed in all cases. They are tonal for  ${M}\geq 0.75$ and broaden for lower Mach numbers. They are associated with the azimuthal modes
${M}\geq 0.75$ and broaden for lower Mach numbers. They are associated with the azimuthal modes  $n_{\theta }=0$ to
$n_{\theta }=0$ to  $n_{\theta }^{max}$, with
$n_{\theta }^{max}$, with  $n_{\theta }^{max}=8$ for
$n_{\theta }^{max}=8$ for  ${M}=0.75$ and 1 for
${M}=0.75$ and 1 for  ${M}=2$, for example. Their frequencies do not appreciably vary with the nozzle-exit boundary-layer thickness and turbulence and fall in the frequency bands predicted for the upstream-propagating guided jet waves using a vortex-sheet model. For all azimuthal modes, the peak intensities are highest for the first radial guided jet mode. They increase approximately as
${M}=2$, for example. Their frequencies do not appreciably vary with the nozzle-exit boundary-layer thickness and turbulence and fall in the frequency bands predicted for the upstream-propagating guided jet waves using a vortex-sheet model. For all azimuthal modes, the peak intensities are highest for the first radial guided jet mode. They increase approximately as  ${M}^8$ for
${M}^8$ for  ${M}\leq 1$ and as
${M}\leq 1$ and as  ${M}^3$ for
${M}^3$ for  ${M}\geq 1$, following the scaling laws of jet noise, suggesting that they mainly result from a band-pass filtering of the upstream-travelling sound waves by the guided jet modes. In support of this, the Mach number variations of the peak width and sharpness are explained by the eigenfunctions of the guided waves. Moreover, it appears that, for high subsonic Mach numbers, among the waves possibly resonating in the potential core, only those close to the cutoff frequencies of the guided jet modes can contribute to the near-nozzle peaks. Finally, the peaks are detectable in the far field for large radiation angles. For
${M}\geq 1$, following the scaling laws of jet noise, suggesting that they mainly result from a band-pass filtering of the upstream-travelling sound waves by the guided jet modes. In support of this, the Mach number variations of the peak width and sharpness are explained by the eigenfunctions of the guided waves. Moreover, it appears that, for high subsonic Mach numbers, among the waves possibly resonating in the potential core, only those close to the cutoff frequencies of the guided jet modes can contribute to the near-nozzle peaks. Finally, the peaks are detectable in the far field for large radiation angles. For  ${M}= 0.90$, for instance, they emerge for angles higher than
${M}= 0.90$, for instance, they emerge for angles higher than  $135^\circ$.
$135^\circ$.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 51
- Cited by


