Article contents
An example where lubrication theory comes short: hydraulic jumps in a flow down an inclined plate
Published online by Cambridge University Press: 29 December 2014
Abstract
We examine two-dimensional flows of a viscous liquid on an inclinedplate. If the upstream depth 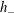 $h_{-}$ of the liquid is larger than its downstream depth
$h_{-}$ of the liquid is larger than its downstream depth 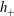 $h_{+}$ , a smooth hydraulic jump (bore) forms and starts propagating down the slope. If the inclination angle of the plate is small, the bore can be described by the so-called lubrication theory. In this work we demonstrate that bores with
$h_{+}$ , a smooth hydraulic jump (bore) forms and starts propagating down the slope. If the inclination angle of the plate is small, the bore can be described by the so-called lubrication theory. In this work we demonstrate that bores with  $h_{+}/h_{-}<(\sqrt{3}-1)/2$ either are unstable or do not exist as steady solutions of the governing equation (physically, these two possibilities are difficult to distinguish). The instability/evolution occurs near a stagnation point and, generally, causes overturning – sometimes on the scale of the whole bore, sometimes on a shorter, local scale. The overturning occurs because the flow advects disturbances towards the stagnation point and, thus, ‘compresses’ them, increasing the slope of the free surface. Interestingly, this effect is not captured by the lubrication theory, which formally yields a well-behaved stable solution for all values of
$h_{+}/h_{-}<(\sqrt{3}-1)/2$ either are unstable or do not exist as steady solutions of the governing equation (physically, these two possibilities are difficult to distinguish). The instability/evolution occurs near a stagnation point and, generally, causes overturning – sometimes on the scale of the whole bore, sometimes on a shorter, local scale. The overturning occurs because the flow advects disturbances towards the stagnation point and, thus, ‘compresses’ them, increasing the slope of the free surface. Interestingly, this effect is not captured by the lubrication theory, which formally yields a well-behaved stable solution for all values of 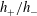 $h_{+}/h_{-}$ .
$h_{+}/h_{-}$ .
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 3
- Cited by


