Article contents
Boundary layers in Helmholtz flows
Published online by Cambridge University Press: 11 November 2019
Abstract
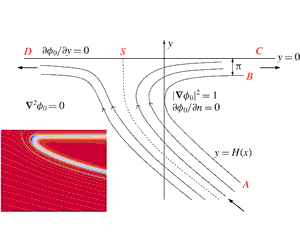
Recent comparisons between classical Wagner theory for the impact of two liquid droplets and direct numerical simulations in Cimpeanu & Moore (J. Fluid Mech., vol. 856, 2018, pp. 764–796) show that, in some regimes, the inviscid theory over-predicts the thickness of the root of the splash jet that forms in the impact, while also struggling to predict the angle at which the jet is emitted. The effect of capillary and viscous perturbations to Helmholtz flows was investigated in a previous study, see Moore et al. (J. Fluid Mech., vol. 742, 2014, R1). However, the paper in question ignored a term in the second-order perturbation analysis, which needs to be included in order to predict the displacement of the inviscid free boundary to lowest order. In this paper, we derive a singular integro-differential equation for the free-surface perturbations caused by viscosity in Helmholtz flows and discuss its application both in the context of Wagner theory and more generally. In particular, viscosity can induce non-monotonic behaviour in the free boundary profiles near points of maximum curvature.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
Footnotes
Article last updated 07 March 2023
References
- 1
- Cited by


