Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Nakayama, Keisuke
Shintani, Tetsuya
Kokubo, Kazuki
Kakinuma, Taro
Maruya, Yasuyuki
Komai, Katsuaki
and
Okada, Tomonari
2012.
Residual currents over a uniform slope due to breaking of internal waves in a two‐layer system.
Journal of Geophysical Research: Oceans,
Vol. 117,
Issue. C10,
NAKAYAMA, Keisuke
KOKUBO, Kazuki
SHINTANI, Tetsuya
OTSUKA, Jyunichi
MARUYA, Yasuyuki
WATANABE, Yasunori
KOMAI, Katsuaki
and
OKADA, Tomonari
2012.
Current induced by breaking of internal Kelvin waves.
Journal of Japan Society of Civil Engineers, Ser. B2 (Coastal Engineering),
Vol. 68,
Issue. 2,
p.
I_926.
NAKAYAMA, Keisuke
SHINTANI, Tetsuya
SHIMIZU, Kenji
KISHITA, Naoki
OKADA, Tomonari
SATO, Yukinobu
MARUYA, Yasuyuki
and
KOMAI, Katsuaki
2013.
MESH ASPECT RATIO AND NON-HYDROSTATIC EFFECT ON INTERNAL WAVE BREAKING IN TOKYO BAY.
Journal of Japan Society of Civil Engineers, Ser. B3 (Ocean Engineering),
Vol. 69,
Issue. 2,
p.
I_742.
Subich, Christopher J.
Lamb, Kevin G.
and
Stastna, Marek
2013.
Simulation of the Navier–Stokes equations in three dimensions with a spectral collocation method.
International Journal for Numerical Methods in Fluids,
Vol. 73,
Issue. 2,
p.
103.
KOKUBO, Kazuki
NAKAYAMA, Keisuke
SHINTANI, Tetsuya
KAKINUMA, Taro
OTSUKA, Jyunichi
WATANABE, Yasunori
KOMAI, Katsuaki
and
SHIMIZU, Kenji
2013.
Mechanisms of Horizontal Circulation Induced by Breaking of Internal Kelvin Waves.
Journal of Japan Society of Civil Engineers, Ser. B2 (Coastal Engineering),
Vol. 69,
Issue. 2,
p.
I_451.
Arthur, Robert S.
and
Fringer, Oliver B.
2014.
The dynamics of breaking internal solitary waves on slopes.
Journal of Fluid Mechanics,
Vol. 761,
Issue. ,
p.
360.
Lamb, Kevin G.
and
Xiao, Wenting
2014.
Internal solitary waves shoaling onto a shelf: Comparisons of weakly-nonlinear and fully nonlinear models for hyperbolic-tangent stratifications.
Ocean Modelling,
Vol. 78,
Issue. ,
p.
17.
Bourgault, D.
Morsilli, M.
Richards, C.
Neumeier, U.
and
Kelley, D.E.
2014.
Sediment resuspension and nepheloid layers induced by long internal solitary waves shoaling orthogonally on uniform slopes.
Continental Shelf Research,
Vol. 72,
Issue. ,
p.
21.
Olsthoorn, Jason
and
Stastna, Marek
2014.
Numerical investigation of internal wave‐induced sediment motion: Resuspension versus entrainment.
Geophysical Research Letters,
Vol. 41,
Issue. 8,
p.
2876.
Lamb, Kevin G.
2014.
Internal Wave Breaking and Dissipation Mechanisms on the Continental Slope/Shelf.
Annual Review of Fluid Mechanics,
Vol. 46,
Issue. 1,
p.
231.
Verschaeve, Joris C. G.
and
Pedersen, Geir K.
2014.
Linear stability of boundary layers under solitary waves.
Journal of Fluid Mechanics,
Vol. 761,
Issue. ,
p.
62.
Aghsaee, Payam
and
Boegman, Leon
2015.
Experimental investigation of sediment resuspension beneath internal solitary waves of depression.
Journal of Geophysical Research: Oceans,
Vol. 120,
Issue. 5,
p.
3301.
Harnanan, Sandhya
Soontiens, Nancy
and
Stastna, Marek
2015.
Internal wave boundary layer interaction: A novel instability over broad topography.
Physics of Fluids,
Vol. 27,
Issue. 1,
Sutherland, B. R.
Keating, S.
and
Shrivastava, I.
2015.
Transmission and reflection of internal solitary waves incident upon a triangular barrier.
Journal of Fluid Mechanics,
Vol. 775,
Issue. ,
p.
304.
Al-Awwad, Saad Fahd
and
Pomar, Luis
2015.
Origin of the rudstone–floatstone beds in the Upper Jurassic Arab-D reservoir, Khurais Complex, Saudi Arabia.
Marine and Petroleum Geology,
Vol. 67,
Issue. ,
p.
743.
Soontiens, Nancy
Stastna, Marek
and
Waite, Michael L.
2015.
Topographically generated internal waves and boundary layer instabilities.
Physics of Fluids,
Vol. 27,
Issue. 8,
NAKAYAMA, Keisuke
YOSHIE, Yuto
SHINTANI, Tetsuya
KAKINUMA, Taro
NGUYEN, Hoang Duc
SATO, Yukinobu
and
KOMAI, Katsuaki
2015.
ANALYSIS OF WIND-INDUCED RESPONSE OF A STRATIFIED LAKE BY FULLY-NONLINEAR AND STRONGLY-DISPERSIVE THREE-LAYER MODEL.
Journal of Japan Society of Civil Engineers, Ser. B1 (Hydraulic Engineering),
Vol. 71,
Issue. 4,
p.
I_793.
Zhu, Hai
Wang, Lingling
Avital, E.J.
Tang, Hongwu
and
Williams, J.J.R.
2016.
Numerical simulation of interaction between internal solitary waves and submerged ridges.
Applied Ocean Research,
Vol. 58,
Issue. ,
p.
118.
Xu, Chengzhu
Subich, Christopher
and
Stastna, Marek
2016.
Numerical simulations of shoaling internal solitary waves of elevation.
Physics of Fluids,
Vol. 28,
Issue. 7,
NAKAYAMA, Keisuke
SATO, Takahiro
BOEGMAN, Leon
and
SHIMIZU, Kenji
2017.
CATEGORIZATION OF INTERNAL SOLITARY WAVE BREAKINGS ON A UNIFORM SLOPE.
Journal of Japan Society of Civil Engineers, Ser. B2 (Coastal Engineering),
Vol. 73,
Issue. 2,
p.
I_31.
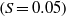 and steep
and steep 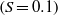 slopes. Over a flat bottom, the potential for vortex shedding is shown to be directly dependent on wave amplitude, for a particular stratification, owing to increase of the adverse pressure gradient (
slopes. Over a flat bottom, the potential for vortex shedding is shown to be directly dependent on wave amplitude, for a particular stratification, owing to increase of the adverse pressure gradient (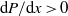 for leftward propagating waves) beneath the trailing edge of larger amplitude waves. The generated eddies can ascend from the bottom boundary to as high as 33 % of the total depth in two-dimensional simulations. Over sloping boundaries, global instability occurs beneath all waves as they steepen. For the slopes considered, vortex shedding begins before wave breaking and the vortices, shed from the bottom boundary, can reach the pycnocline, modifying the wave breaking mechanism. Combining the results over flat and sloping boundaries, a unified criterion for vortex shedding in arbitrary two-layer continuous stratifications is proposed, which depends on the momentum-thickness Reynolds number and the non-dimensionalized ISW-induced pressure gradient at the point of separation. The criterion is generalized to a form that may be readily computed from field data and compared to published laboratory experiments and field observations. During vortex shedding events, the bed shear stress, vertical velocity and near-bed Reynolds stress were elevated, in agreement with laboratory observations during re-suspension events, indicating that boundary layer instability is an important mechanism leading to sediment re-suspension.
for leftward propagating waves) beneath the trailing edge of larger amplitude waves. The generated eddies can ascend from the bottom boundary to as high as 33 % of the total depth in two-dimensional simulations. Over sloping boundaries, global instability occurs beneath all waves as they steepen. For the slopes considered, vortex shedding begins before wave breaking and the vortices, shed from the bottom boundary, can reach the pycnocline, modifying the wave breaking mechanism. Combining the results over flat and sloping boundaries, a unified criterion for vortex shedding in arbitrary two-layer continuous stratifications is proposed, which depends on the momentum-thickness Reynolds number and the non-dimensionalized ISW-induced pressure gradient at the point of separation. The criterion is generalized to a form that may be readily computed from field data and compared to published laboratory experiments and field observations. During vortex shedding events, the bed shear stress, vertical velocity and near-bed Reynolds stress were elevated, in agreement with laboratory observations during re-suspension events, indicating that boundary layer instability is an important mechanism leading to sediment re-suspension.
