Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Donzis, Diego A.
Gibbon, John D.
Gupta, Anupam
Kerr, Robert M.
Pandit, Rahul
and
Vincenzi, Dario
2013.
Vorticity moments in four numerical simulations of the 3D Navier–Stokes equations.
Journal of Fluid Mechanics,
Vol. 732,
Issue. ,
p.
316.
Gibbon, John D
Donzis, Diego A
Gupta, Anupam
Kerr, Robert M
Pandit, Rahul
and
Vincenzi, Dario
2014.
Regimes of nonlinear depletion and regularity in the 3D Navier–Stokes equations.
Nonlinearity,
Vol. 27,
Issue. 10,
p.
2605.
Luo, Guo
and
Hou, Thomas Y.
2014.
Potentially singular solutions of the 3D axisymmetric Euler equations.
Proceedings of the National Academy of Sciences,
Vol. 111,
Issue. 36,
p.
12968.
Luo, Guo
and
Hou, Thomas Y.
2014.
Toward the Finite-Time Blowup of the 3D Axisymmetric Euler Equations: A Numerical Investigation.
Multiscale Modeling & Simulation,
Vol. 12,
Issue. 4,
p.
1722.
Mulungye, Rachel M.
Lucas, Dan
and
Bustamante, Miguel D.
2015.
Symmetry-plane model of 3D Euler flows and mapping to regular systems to improve blowup assessment using numerical and analytical solutions.
Journal of Fluid Mechanics,
Vol. 771,
Issue. ,
p.
468.
Agafontsev, D. S.
Kuznetsov, E. A.
and
Mailybaev, A. A.
2015.
Development of high vorticity structures in incompressible 3D Euler equations.
Physics of Fluids,
Vol. 27,
Issue. 8,
Childress, Stephen
Gilbert, Andrew D.
and
Valiant, Paul
2016.
Eroding dipoles and vorticity growth for Euler flows in : axisymmetric flow without swirl.
Journal of Fluid Mechanics,
Vol. 805,
Issue. ,
p.
1.
Hou, Thomas Y.
and
Liu, Pengfei
2016.
Handbook of Mathematical Analysis in Mechanics of Viscous Fluids.
p.
1.
Ayala, Diego
and
Protas, Bartosz
2017.
Extreme vortex states and the growth of enstrophy in three-dimensional incompressible flows.
Journal of Fluid Mechanics,
Vol. 818,
Issue. ,
p.
772.
Agafontsev, D. S.
Kuznetsov, E. A.
and
Mailybaev, A. A.
2017.
Asymptotic solution for high-vorticity regions in incompressible three-dimensional Euler equations.
Journal of Fluid Mechanics,
Vol. 813,
Issue. ,
Larios, Adam
Petersen, Mark R.
Titi, Edriss S.
and
Wingate, Beth
2018.
A computational investigation of the finite-time blow-up of the 3D incompressible Euler equations based on the Voigt regularization.
Theoretical and Computational Fluid Dynamics,
Vol. 32,
Issue. 1,
p.
23.
Kerr, Robert M.
2018.
Enstrophy and circulation scaling for Navier–Stokes reconnection.
Journal of Fluid Mechanics,
Vol. 839,
Issue. ,
Hou, Thomas Yizhao
and
Liu, Pengfei
2018.
Handbook of Mathematical Analysis in Mechanics of Viscous Fluids.
p.
869.
Gibbon, John D.
Gupta, Anupam
Pal, Nairita
and
Pandit, Rahul
2018.
The role of BKM-type theorems in 3D Euler, Navier–Stokes and Cahn–Hilliard–Navier–Stokes analysis.
Physica D: Nonlinear Phenomena,
Vol. 376-377,
Issue. ,
p.
60.
Campolina, Ciro S.
and
Mailybaev, Alexei A.
2018.
Chaotic Blowup in the 3D Incompressible Euler Equations on a Logarithmic Lattice.
Physical Review Letters,
Vol. 121,
Issue. 6,
Agafontsev, D. S.
Kuznetsov, E. A.
and
Mailybaev, A. A.
2018.
Development of high vorticity structures and geometrical properties of the vortex line representation.
Physics of Fluids,
Vol. 30,
Issue. 9,
Childress, Stephen
and
Gilbert, Andrew D
2018.
Eroding dipoles and vorticity growth for Euler flows in ${{\mathbb{R}}}^{3}$: the hairpin geometry as a model for finite-time blowup.
Fluid Dynamics Research,
Vol. 50,
Issue. 1,
p.
011418.
Luo, Guo
and
Hou, Thomas Y.
2019.
Formation of Finite-Time Singularities in the 3D Axisymmetric Euler Equations: A Numerics Guided Study.
SIAM Review,
Vol. 61,
Issue. 3,
p.
793.
Kang, Di
Yun, Dongfang
and
Protas, Bartosz
2020.
Maximum amplification of enstrophy in three-dimensional Navier–Stokes flows.
Journal of Fluid Mechanics,
Vol. 893,
Issue. ,
Yao, Jie
and
Hussain, Fazle
2020.
On singularity formation via viscous vortex reconnection.
Journal of Fluid Mechanics,
Vol. 888,
Issue. ,
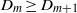 ${D}_{m} \geq {D}_{m+ 1} $ , the reverse of the usual
${D}_{m} \geq {D}_{m+ 1} $ , the reverse of the usual 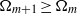 ${\Omega }_{m+ 1} \geq {\Omega }_{m} $ Hölder ordering of the original moments. Two temporal phases have been identified for the Euler calculations. In the first phase the
${\Omega }_{m+ 1} \geq {\Omega }_{m} $ Hölder ordering of the original moments. Two temporal phases have been identified for the Euler calculations. In the first phase the 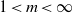 $1\lt m\lt \infty $ vorticity moments are ordered in a manner consistent with the new Navier–Stokes hierarchy and grow in a manner that skirts the lower edge of possible singular growth with
$1\lt m\lt \infty $ vorticity moments are ordered in a manner consistent with the new Navier–Stokes hierarchy and grow in a manner that skirts the lower edge of possible singular growth with 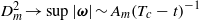 ${ D}_{m}^{2} \rightarrow \sup \vert \boldsymbol{\omega} \vert \sim A_{m}{({T}_{c} - t)}^{- 1} $ where the
${ D}_{m}^{2} \rightarrow \sup \vert \boldsymbol{\omega} \vert \sim A_{m}{({T}_{c} - t)}^{- 1} $ where the 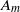 ${A}_{m} $ are nearly independent of
${A}_{m} $ are nearly independent of 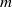 $m$ . In the second phase, the new
$m$ . In the second phase, the new 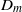 ${D}_{m} $ ordering breaks down as the
${D}_{m} $ ordering breaks down as the 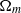 ${\Omega }_{m} $ converge towards the same super-exponential growth for all
${\Omega }_{m} $ converge towards the same super-exponential growth for all 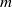 $m$ . The transition is identified using new inequalities for the upper bounds for the
$m$ . The transition is identified using new inequalities for the upper bounds for the 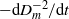 $- \mathrm{d} { D}_{m}^{- 2} / \mathrm{d} t$ that are based solely upon the ratios
$- \mathrm{d} { D}_{m}^{- 2} / \mathrm{d} t$ that are based solely upon the ratios 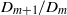 ${D}_{m+ 1} / {D}_{m} $ , and the convergent super-exponential growth is shown by plotting
${D}_{m+ 1} / {D}_{m} $ , and the convergent super-exponential growth is shown by plotting 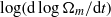 $\log (\mathrm{d} \log {\Omega }_{m} / \mathrm{d} t)$ . Three-dimensional graphics show significant divergence of the vortex lines during the second phase, which could be what inhibits the initial power-law growth.
$\log (\mathrm{d} \log {\Omega }_{m} / \mathrm{d} t)$ . Three-dimensional graphics show significant divergence of the vortex lines during the second phase, which could be what inhibits the initial power-law growth.
