Article contents
Bubble and conical forms of vortex breakdown in swirling jets
Published online by Cambridge University Press: 24 June 2019
Abstract
Experimental investigations of laminar swirling jets had revealed a new form of vortex breakdown, named conical vortex breakdown, in addition to the commonly observed bubble form. The present study explores these breakdown states that develop for the Maxworthy profile (a model of swirling jets) at inflow, from streamwise-invariant initial conditions, with direct numerical simulations. For a constant Reynolds number based on jet radius and a centreline velocity of 200, various flow states were observed as the inflow profile’s swirl parameter 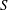 $S$ (scaled centreline radial derivative of azimuthal velocity) was varied up to 2. At low swirl (
$S$ (scaled centreline radial derivative of azimuthal velocity) was varied up to 2. At low swirl (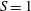 $S=1$) a helical mode of azimuthal wavenumber
$S=1$) a helical mode of azimuthal wavenumber 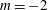 $m=-2$ (co-winding, counter-rotating mode) was observed. A ‘swelling’ appeared at
$m=-2$ (co-winding, counter-rotating mode) was observed. A ‘swelling’ appeared at 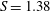 $S=1.38$, and a steady bubble breakdown at
$S=1.38$, and a steady bubble breakdown at 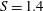 $S=1.4$. On further increase to
$S=1.4$. On further increase to 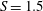 $S=1.5$, a helical, self-excited global mode (
$S=1.5$, a helical, self-excited global mode (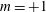 $m=+1$, counter-winding and co-rotating) was observed, originating in the bubble’s wake but with little effect on the bubble itself – a bubble vortex breakdown with a spiral tail. Local and global stability analyses revealed this to arise from a linear instability mechanism, distinct from that for the spiral breakdown which has been studied using Grabowski profile (a model of wing-tip vortices). At still higher swirl (
$m=+1$, counter-winding and co-rotating) was observed, originating in the bubble’s wake but with little effect on the bubble itself – a bubble vortex breakdown with a spiral tail. Local and global stability analyses revealed this to arise from a linear instability mechanism, distinct from that for the spiral breakdown which has been studied using Grabowski profile (a model of wing-tip vortices). At still higher swirl (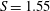 $S=1.55$), a pulsating type of bubble breakdown occurred, followed by conical breakdown at 1.6. The latter consists of a large toroidal vortex confined by a radially expanding conical sheet, and a weaker vortex core downstream. For the highest swirls, the sheet was no longer conical, but curved away from the axis as a wide-open breakdown. The applicability of two classical inviscid theories for vortex breakdown – transition to a conjugate state, and the dominance of negative azimuthal vorticity – was assessed for the conical form. As required by the former, the flow transitioned from a supercritical to subcritical state in the vicinity of the stagnation point. The deviations from the predictions of the latter model were considerable.
$S=1.55$), a pulsating type of bubble breakdown occurred, followed by conical breakdown at 1.6. The latter consists of a large toroidal vortex confined by a radially expanding conical sheet, and a weaker vortex core downstream. For the highest swirls, the sheet was no longer conical, but curved away from the axis as a wide-open breakdown. The applicability of two classical inviscid theories for vortex breakdown – transition to a conjugate state, and the dominance of negative azimuthal vorticity – was assessed for the conical form. As required by the former, the flow transitioned from a supercritical to subcritical state in the vicinity of the stagnation point. The deviations from the predictions of the latter model were considerable.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
Moise and Mathew supplementary movie 1
Axial velocity contours on z = 0 plane at different times for the pulsating BVB observed at S = 1.56. The low frequency modulations associated with the unsteady flow can be observed from the figure, which is a characteristic of the pulsating type of BVB.
Moise and Mathew supplementary movie 2
Temporal evolution of three-dimensional streamlines based on instantaneous velocity fields is shown for pulsating BVB observed at S = 1.56. The intermittent formation of a closed set of streamlines that delineate a toroidal structure are correlated with the pulsating temporal behaviour characteristic of this flow. It is noted that the streamlines originate from equispaced points along the line segment y = -0.5 to 0.5 for x = 3.5 and z = 0. The toroidal structure observed is the intermittent ‘second cell’ while the other permanent toroidal structure associated with the bubble is not highlighted here for clarity, but can be seen in figure 8.
Moise and Mathew supplementary movie 3
Temporal evolution for the case of S = 1.6 shown using axial velocity contours on z = 0 plane at different times. Past initial transients, a long-time state of CVB can be observed starting from approximately t = 3000. The dynamic features and slow temporal changes in the conical sheet’s structure can be observed.
Moise and Mathew supplementary movie 4
Cross-sectional features of CVB at S = 1.6 are highlighted using axial velocity contours plane at different times. The flow remains axisymmetric in the upstream regions, but non-axisymmetric features can be observed downstream. The conical sheet is seen to slowly rotate with time.
- 28
- Cited by


