Article contents
Bubble entrainment and liquid–bubble interaction under unsteady breaking waves
Published online by Cambridge University Press: 26 November 2014
Abstract
Liquid–bubble interaction, especially in complex two-phase bubbly flow under breaking waves, is still poorly understood. In the present study, we perform a large-eddy simulation using a Navier–Stokes solver extended to incorporate entrained bubble populations, using an Eulerian–Eulerian formulation for a polydisperse bubble phase. The volume-of-fluid method is used for free-surface tracking. We consider an isolated unsteady deep water breaking event generated by a focused wavepacket. Bubble contributions to dissipation and momentum transfer between the water and air phases are considered. The model is shown to predict free-surface evolution, mean and turbulent velocities, and integral properties of the entrained dispersed bubbles fairly well. We investigate turbulence modulation by dispersed bubbles as well as shear- and bubble-induced dissipation, in both spilling and plunging breakers. We find that the total bubble-induced dissipation accounts for more than 50 % of the total dissipation in the breaking region. The average dissipation rate per unit length of breaking crest is usually written as 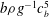 $b{\it\rho}g^{-1}c_{b}^{5}$ , where
$b{\it\rho}g^{-1}c_{b}^{5}$ , where 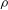 ${\it\rho}$ is the water density,
${\it\rho}$ is the water density, 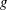 $g$ is the gravitational acceleration and
$g$ is the gravitational acceleration and 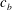 $c_{b}$ is the phase speed of the breaking wave. The breaking parameter,
$c_{b}$ is the phase speed of the breaking wave. The breaking parameter, 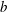 $b$ , has been poorly constrained by experiments and field measurements. We examine the time-dependent evolution of
$b$ , has been poorly constrained by experiments and field measurements. We examine the time-dependent evolution of  $b$ for both constant-steepness and constant-amplitude wavepackets. A scaling law for the averaged breaking parameter is obtained. The exact two-phase transport equation for turbulent kinetic energy (TKE) is compared with the conventional single-phase transport equation, and it is found that the former overpredicts the total subgrid-scale dissipation and turbulence production by mean shear during active breaking. All of the simulations are also repeated without the inclusion of a dispersed bubble phase, and it is shown that the integrated TKE in the breaking region is damped by the dispersed bubbles by approximately 20 % for a large plunging breaker to 50 % for spilling breakers. In the plunging breakers, the TKE is damped slightly or even enhanced during the initial stage of active breaking.
$b$ for both constant-steepness and constant-amplitude wavepackets. A scaling law for the averaged breaking parameter is obtained. The exact two-phase transport equation for turbulent kinetic energy (TKE) is compared with the conventional single-phase transport equation, and it is found that the former overpredicts the total subgrid-scale dissipation and turbulence production by mean shear during active breaking. All of the simulations are also repeated without the inclusion of a dispersed bubble phase, and it is shown that the integrated TKE in the breaking region is damped by the dispersed bubbles by approximately 20 % for a large plunging breaker to 50 % for spilling breakers. In the plunging breakers, the TKE is damped slightly or even enhanced during the initial stage of active breaking.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 89
- Cited by


