Hostname: page-component-5b777bbd6c-6lqsf Total loading time: 0 Render date: 2025-06-18T14:37:54.543Z Has data issue: false hasContentIssue false
  • English
  • Français

Cargo carrying by a spring connected chiral micro-swimmer in a square channel

Published online by Cambridge University Press:  22 May 2025

Xiao Hu Open the ORCID record for Xiao Hu [Opens in a new window] ,
Weijin Chen ,
Zuchao Zhu ,
Jianzhong Lin Open the ORCID record for Jianzhong Lin [Opens in a new window] ,
Deming Nie Open the ORCID record for Deming Nie [Opens in a new window]  and
Yan Xia Open the ORCID record for Yan Xia [Opens in a new window]
Xiao Hu
Affiliation:
Zhejiang Key Laboratory of Multiflow and Fluid Machinery, Zhejiang Sci-Tech University, Hangzhou, Zhejiang 310018, PR China
Weijin Chen
Affiliation:
Zhejiang Key Laboratory of Multiflow and Fluid Machinery, Zhejiang Sci-Tech University, Hangzhou, Zhejiang 310018, PR China
Zuchao Zhu*
Affiliation:
Zhejiang Key Laboratory of Multiflow and Fluid Machinery, Zhejiang Sci-Tech University, Hangzhou, Zhejiang 310018, PR China
Jianzhong Lin*
Affiliation:
Department of Mechanics, State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou, Zhejiang 310027, PR China
Deming Nie
Affiliation:
Zhejiang Provincial Key Laboratory of Flow Measurement Technology, China Jiliang University, Hangzhou, Zhejiang 310027, PR China
Yan Xia
Affiliation:
Graduate School of Biomedical Engineering, Tohoku University, Sendai, Japan
*
Corresponding authors: Zuchao Zhu, zhuzuchao@zstu.edu.cn; Jianzhong Lin, mecjzlin@public.zju.edu.cn
Corresponding authors: Zuchao Zhu, zhuzuchao@zstu.edu.cn; Jianzhong Lin, mecjzlin@public.zju.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

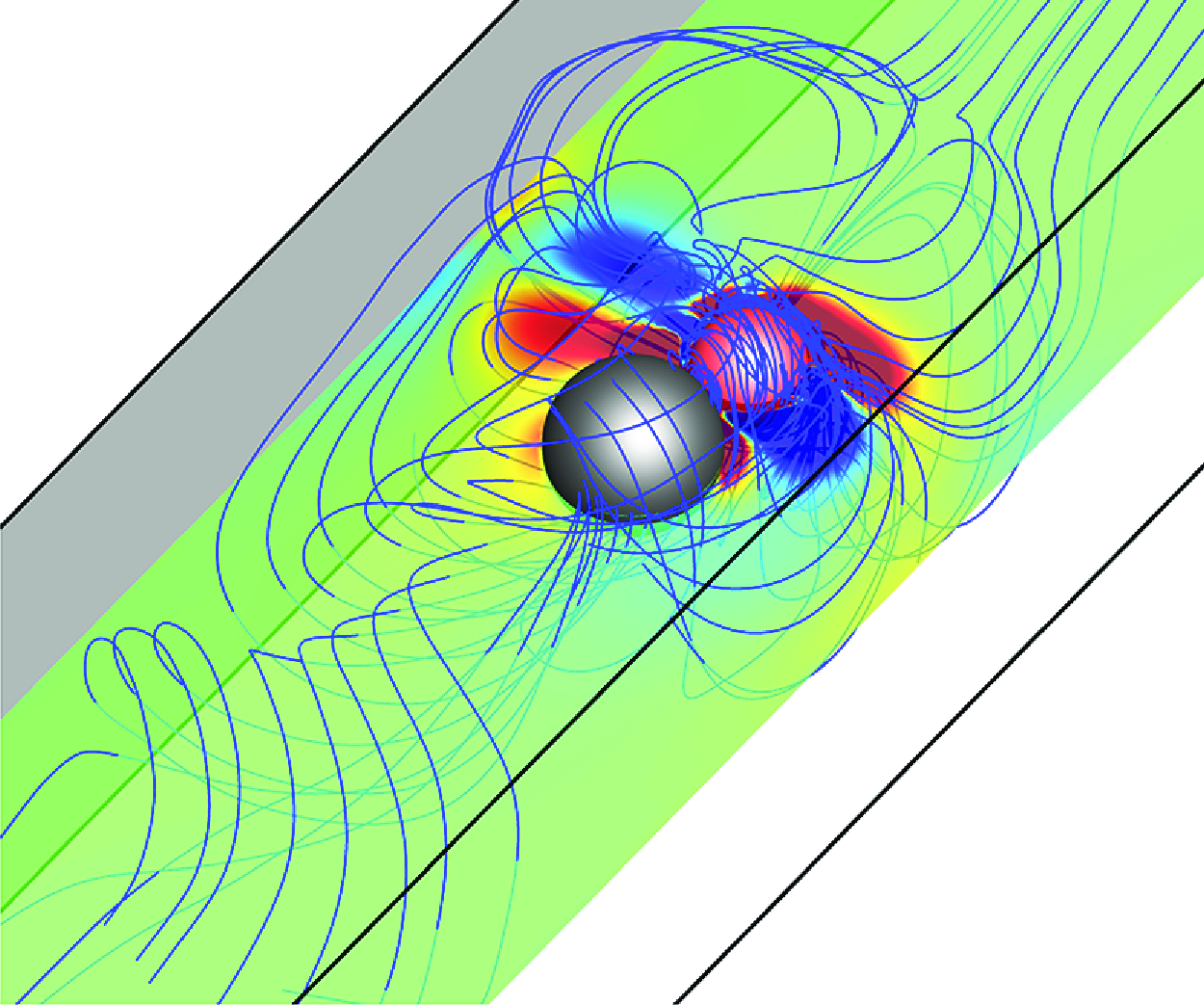
Cargo carrying by a spring connected chiral micro-swimmer in a square channel is numerical studied by the three-dimensional lattice Boltzmann method and a chiral squirmer model. The effects of the driving type (β), swimming Reynolds number (Rep), spin coefficient (ξ) and diameter ratio (S) on the changes of the cargo-carrying velocity, spring length and motion modes are investigated, respectively. Four kinds of interesting motion modes are observed. When the chirality is not considered, the optimal combination for maximising swimming velocity are the pusher–cargo and cargo–puller configurations when Rep = 0.1 ∼ 1. When Rep is enhanced, the swimming velocities of the pusher–cargo, puller–cargo and cargo–pusher are increased, while the velocity of the cargo–puller is gradually decreased. When considering the chirality, only the swimming velocity of cargo–pusher and cargo–puller keep an interesting increment, and the reverse motion mode for the pusher-cargo and puller-cargo is firstly found in the present work when ξ exceeds a certain value. The impact of S on the cargo-carrying behaviour is complex, three kinds of oscillatory trajectories will appear under different ξ and S. The swimming velocity is reduced and even zero velocity will be observed when S is large. This work reveals key factors on the movement of microorganisms, offering guidance for improving cargo-carrying capabilities.

JFM classification

Biological Fluid Dynamics: Micro-organism dynamics Micro-/Nano-fluid dynamics: Microscale transport
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1011 , 25 May 2025 , A50
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Akolpoglu, M.B., Alapan, Y., Dogan, N.O., Baltaci, S.F., Yasa, O., Tural, G.A. & Sitti, M. 2022 Magnetically steerable bacterial microrobots moving in 3d biological matrices for stimuli-responsive cargo delivery. Sci. Adv. 8 (28), eabo6163.10.1126/sciadv.abo6163CrossRefGoogle ScholarPubMed
Bazzi, S., Shammas, E., Asmar, D. & Mason, M.T. 2017 Motion analysis of two-link nonholonomic swimmers. Nonlinear Dyn. 89 (4), 2739–2751.10.1007/s11071-017-3622-yCrossRefGoogle Scholar
Binagia, J.P. & Shaqfeh, E.S.G. 2021 Self-propulsion of a freely suspended swimmer by a swirling tail in a viscoelastic fluid. Phys. Rev. Fluids 6 (5), 053301.10.1103/PhysRevFluids.6.053301CrossRefGoogle Scholar
Blake, J.R. 1971 A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46 (1), 199–208.10.1017/S002211207100048XCrossRefGoogle Scholar
Brody, H. 2018 Gene therapy. Nature 564 (7735), S5–S5.10.1038/d41586-018-07639-9CrossRefGoogle ScholarPubMed
Burada, P.S., Maity, R. & Jülicher, F. 2022 Hydrodynamics of chiral squirmers. Phys. Rev. E 105 (2), 024603.10.1103/PhysRevE.105.024603CrossRefGoogle ScholarPubMed
Carena, L.N., Gonnella, G., Marenduzzo, D. & Negro, G. 2019 Rotation and propulsion in 3D active chiral droplets. Proc. Natl Acad. Sci. USA 116 (44), 22065–22070.10.1073/pnas.1910909116CrossRefGoogle Scholar
Cates, M.E. & Mackintosh, F.C. 2011 Active soft matter. Soft Matt. 7 (7), 3050.10.1039/c1sm90014eCrossRefGoogle Scholar
Chaithanya, K.V.S. & Thampi, S.P. 2021 Wall-curvature driven dynamics of a microswimmer. Phys. Rev. Fluids 6 (8), 083101.Google Scholar
Clopés, J., Gompper, G. & Winkler, R.G. 2020 Hydrodynamic interactions in squirmer dumbbells: active stress-induced alignment and locomotion. Soft Matt. 16 (47), 10676–10687.10.1039/D0SM01569ECrossRefGoogle ScholarPubMed
Collis, J.F., Chakraborty, D. & Sader, J.E. 2017 Autonomous propulsion of nanorods trapped in an acoustic field. J. Fluid Mech. 825, 29–48.10.1017/jfm.2017.381CrossRefGoogle Scholar
Darnton, N.C., Turner, L., Rojevsky, S. & Berg, H.C. 2006 On torque and tumbling in swimming Escherichia coli . J. Bacteriol. 189 (5), 1756–1764.10.1128/JB.01501-06CrossRefGoogle ScholarPubMed
Debnath, T. & Ghosh, P. 2018 Activated barrier crossing dynamics of a Janus particle carrying cargo. Phys. Chem. Chem. Phys. 20 (38), 25069–25077.10.1039/C8CP04419HCrossRefGoogle Scholar
Dombrowski, T., Nguyen, H. & Klotsa, D. 2022 Pairwise interactions between model swimmers at intermediate Reynolds numbers. Phys. Rev. Fluids 7 (7), 074401.10.1103/PhysRevFluids.7.074401CrossRefGoogle Scholar
Donaldson, G.P., Lee, S.M. & Mazmanian, S.K. 2015 Gut biogeography of the bacterial microbiota. Nat. Rev. Microbiol. 14 (1), 20–32.10.1038/nrmicro3552CrossRefGoogle ScholarPubMed
Fadda, F., Molina, J.J. & Yamamoto, R. 2020 Dynamics of a chiral swimmer sedimenting on a flat plate. Phys. Rev. E 101 (5), 052608.10.1103/PhysRevE.101.052608CrossRefGoogle ScholarPubMed
Fauci, L.J. & Dillon, R. 2006 Biofluidmechanics of reproduction. Annu. Rev. Fluid Mech. 38 (1), 371–394.10.1146/annurev.fluid.37.061903.175725CrossRefGoogle Scholar
Friedrich, B.M. & Julicher, F. 2009 Steering chiral swimmers along noisy helical paths. Phys. Rev. Lett. 103 (6), 068102.10.1103/PhysRevLett.103.068102CrossRefGoogle ScholarPubMed
Friedrich, B.M. & Jülicher, F. 2007 Chemotaxis of sperm cells. Proc. Natl Acad. Sci. USA 104 (33), 13256–13261.10.1073/pnas.0703530104CrossRefGoogle ScholarPubMed
Guo, Z., Shi, B. & Wang, N. 2000 Lattice BGK model for incompressible Navier–Stokes equation. J. Comput. Phys. 165 (1), 288–306.10.1006/jcph.2000.6616CrossRefGoogle Scholar
Gutman, E. & Or, Y. 2016 Optimizing an undulating magnetic microswimmer for cargo towing. Phys. Rev. E 93 (6), 063105.10.1103/PhysRevE.93.063105CrossRefGoogle ScholarPubMed
Guzmán, E. & Maestro, A. 2022 Synthetic micro/Nanomotors for drug delivery. Technologies 10 (4), 96.10.3390/technologies10040096CrossRefGoogle Scholar
Howse, J.R., Jones, R.A.L., Ryan, A.J., Gough, T., Vafabakhsh, R. & Goldestanian, R. 2007 Self-Motile Colloidal Particles: From Directed Propulsion to Random Walk. Phys. Rev. Lett. 99 (4), 048102.10.1103/PhysRevLett.99.048102CrossRefGoogle ScholarPubMed
Hu, X., Chen, W., Lin, J., Nie, D., Zhu, Z. & Lin, P. 2024 The motion of micro-swimmers over a cavity in a micro-channel. Soft Matt. 20 (12), 2789–2803.10.1039/D3SM01589KCrossRefGoogle Scholar
Hu, X., Kang, X., Lin, J., Lin, P., Bao, F. & Zhu, Z. 2023 a Comparison of ellipsoidal particle migration in square channel flow of power-law fluids with equivalent spheres. Intl J. Multiphase Flow 167, 104565.10.1016/j.ijmultiphaseflow.2023.104565CrossRefGoogle Scholar
Hu, X., Lin, J.Z., Lin, P.F. & Zhu, Z.C. 2023 b Rigid spheroid migration in square channel flow of power-law fluids. Intl J. Mech. Sci. 274, 108194.10.1016/j.ijmecsci.2023.108194CrossRefGoogle Scholar
Hyon, Y., Marcos, J., Powers, T.R., Stocker, R. & Fu, H.C. 2012 The wiggling trajectories of bacteria. J. Fluid Mech. 705, 58–76.10.1017/jfm.2012.217CrossRefGoogle Scholar
Ishikawa, T. 2019 Stability of a dumbbell micro-swimmer. Micromachines-BASEL 10 (1), 33.10.3390/mi10010033CrossRefGoogle ScholarPubMed
Ishikawa, T. 2023 Fluid dynamics of squirmers and ciliated microorganisms. Annu. Rev. Fluid Mech. 56 (1), 119–145.10.1146/annurev-fluid-121021-042929CrossRefGoogle Scholar
Ishikawa, T. & Hota, M. 2006 Interaction of two swimming paramecia. J. Expl Biol. 209 (22), 4452–4463.10.1242/jeb.02537CrossRefGoogle ScholarPubMed
Ishikawa, T., Pedley, T.J., Drescher, K. & Goldstein, R.E. 2020 Stability of dancing volvox. J. Fluid Mech. 903 (411), A11.10.1017/jfm.2020.613CrossRefGoogle Scholar
Jékely, G., Colombelli, J., Hausen, H., Guy, K., Stelzer, E., Nédelec, F. & Arendt, D. 2008 Mechanism of phototaxis in marine zooplankton. Nature 456 (7220), 395–399.10.1038/nature07590CrossRefGoogle ScholarPubMed
Jiang, M., Li, J. & Liu, Z. 2022 A simple and efficient parallel immersed boundary-lattice Boltzmann method for fully resolved simulations of incompressible settling suspensions. Comput. Fluids 237, 105322.10.1016/j.compfluid.2022.105322CrossRefGoogle Scholar
Jiang, M. & Liu, Z. 2022 A pressure compensation method for lattice boltzmann simulation of particle-laden flows in periodic geometries. Phys. Fluids 34 (8), 082004.10.1063/5.0094937CrossRefGoogle Scholar
Jin, C., Chen, Y., Maass, C.C. & Arnold 2021 Collective entrainment and confinement amplify transport by schooling microswimmers. Phys. Rev. Lett. 127 (8), 088006.10.1103/PhysRevLett.127.088006CrossRefGoogle ScholarPubMed
Kameritsch, P. & Renkawitz, J. 2020 Principles of Leukocyte migration strategies. Trends Cell Biol. 30 (10), 818–832.10.1016/j.tcb.2020.06.007CrossRefGoogle ScholarPubMed
Karita, Y., Limmer, D.T. & Hallatschek, O. 2022 Scale-dependent tipping points of bacterial colonization resistance. Proc. Natl Acad. Sci. USA 119 (7), e2115496119.10.1073/pnas.2115496119CrossRefGoogle ScholarPubMed
Kohutek, F. & Bystricky, B. 2019 Leukocytosis as a negative prognostic factor in patients with lung cancer: Which subpopulation of leukocytes is responsible? Ann. Oncol. 30 (S5), V799.10.1093/annonc/mdz269.008CrossRefGoogle Scholar
Kroo, L., Binagia, J.P., Eckman, N., Prakash, M. & Shaqfeh, E.S.G. 2022 A freely suspended robotic swimmer propelled by viscoelastic normal stresses. J. Fluid Mech. 944, A20.10.1017/jfm.2022.485CrossRefGoogle Scholar
Lallemand, P. & Luo, L.-S. 2003 Lattice Boltzmann method for moving boundaries. J. Comput. Phys. 184 (2), 406–421.10.1016/S0021-9991(02)00022-0CrossRefGoogle Scholar
Lancia, F., Yamamoto, T., Ryabchun, A., Yamaguchi, T., Sano, M. & Katsonis, N. 2019 Reorientation behavior in the helical motility of light-responsive spiral droplets. Nat. Commun. 10 (1), 5238.10.1038/s41467-019-13201-6CrossRefGoogle ScholarPubMed
Lauga, E. & Powers, T.R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72 (9), 096601.10.1088/0034-4885/72/9/096601CrossRefGoogle Scholar
Li, C., Qin, B., Gopinath, A., Arratia, P.E., Thomases, B. & Guy, R.D. 2017 Flagellar swimming in viscoelastic fluids: role of fluid elastic stress revealed by simulations based on experimental data. J. R. Soc. Interface 14 (135), 20170289.10.1098/rsif.2017.0289CrossRefGoogle ScholarPubMed
Li, G., Anca, O. & Ardekani, A.M. 2016 Hydrodynamic interaction of swimming organisms in an inertial regime. Phys. Rev. E 94 (5), 053104.10.1103/PhysRevE.94.053104CrossRefGoogle Scholar
Li, G. & Ardekani, A.M. 2014 Hydrodynamic interaction of microswimmers near a wall. Phys. Rev. E 90 (1), 013010.10.1103/PhysRevE.90.013010CrossRefGoogle ScholarPubMed
Lighthill, M.J. 1952 On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Maths 5 (2), 109–118.10.1002/cpa.3160050201CrossRefGoogle Scholar
Lin, Z. & Gao, T. 2019 Direct-forcing fictitious domain method for simulating non-Brownian active particles. Phys. Rev. E 100 (1), 013304.10.1103/PhysRevE.100.013304CrossRefGoogle ScholarPubMed
Magdanz, V., Medina-Sánchez, M., Schwarz, L., Xu, H., Elgeti, J. & Schmidt, O.G. 2017 Spermatozoa as functional components of robotic microswimmers. Adv. Mater. 29 (24), 1606301.10.1002/adma.201606301CrossRefGoogle ScholarPubMed
Michelin, S. & Lauga, E. 2013 Unsteady feeding and optimal strokes of model ciliates. J. Fluid Mech. 715, 1–31.10.1017/jfm.2012.484CrossRefGoogle Scholar
More, R.V. & Ardekani, A.M. 2020 Motion of an inertial squirmer in a density stratified fluid. J. Fluid Mech. 905, A9.10.1017/jfm.2020.719CrossRefGoogle Scholar
Nassir, M., Levi, M. & Shaked, N.T. 2023 Dynamic 3D Modeling for Human Sperm Motility through the Female Cervical Canal and Uterine Cavity to Predict Sperm Chance of Reaching the Oocyte. Cells 12 (1), 203.10.3390/cells12010203CrossRefGoogle ScholarPubMed
Nie, D., Ying, Y., Guan, G., Lin, J. & Ouyang, Z. 2023 Two-dimensional study on the motion and interactions of squirmers under gravity in a vertical channel. J. Fluid Mech. 960, A31.10.1017/jfm.2023.155CrossRefGoogle Scholar
Ouyang, Z. & Lin, J. 2021 The hydrodynamics of an inertial squirmer rod. Phys. Fluids 33 (7), 073302.10.1063/5.0057974CrossRefGoogle Scholar
Ouyang, Z., Lin, Z., Lin, J., Yu, Z. & Phan-Thien, N. 2023 Cargo carrying with an inertial squirmer in a Newtonian fluid. J. Fluid Mech. 959, A25 10.1017/jfm.2023.126CrossRefGoogle Scholar
Ouyang, Z., Lin, Z., Yu, Z., Lin, J. & Phan-Thien, N. 2022 Hydrodynamics of an inertial squirmer and squirmer dumbbell in a tube. J. Fluid Mech. 939, A32.10.1017/jfm.2022.210CrossRefGoogle Scholar
Pak, O.S. & Lauga, E. 2014 Generalized squirming motion of a sphere. J. Engng Maths 88 (1), 1–28.10.1007/s10665-014-9690-9CrossRefGoogle Scholar
Pak, O.S., Zhu, L., Brandt, L. & Lauga, E. 2012 Micropropulsion and microrheology in complex fluids via symmetry breaking. Phys. Fluids 24 (10), 103102.10.1063/1.4758811CrossRefGoogle Scholar
Pande, J. & Smith, A.-S. 2015 Forces and shapes as determinants of micro-swimming: effect on synchronisation and the utilisation of drag. Soft Matt. 11 (12), 2364–2371.10.1039/C4SM02611JCrossRefGoogle ScholarPubMed
Park, Y., Kim, Y. & Lim, S. 2019 a Locomotion of a single-flagellated bacterium. J. Fluid Mech. 859, 586–612.10.1017/jfm.2018.799CrossRefGoogle Scholar
Park, Y., Kim, Y. & Lim, S. 2019 b Flagellated bacteria swim in circles near a rigid wall. Phys. Rev. 100 (6), 063112.Google Scholar
Pedley, T.J., Brumley, D.R. & Goldstein, R.J. 2016 Squirmers with swirl: a model for Volvox swimming. J. Fluid Mech. 798, 165–186.10.1017/jfm.2016.306CrossRefGoogle Scholar
Pöhnl, R., Popescu, M.N. & Uspal, W.E. 2019 Axisymmetric spheroidal squirmers and self-diffusiophoretic particles. J. Phys.: Condens. Matter 32 (16), 164001.Google Scholar
Puente, J.A., Godínez, F.A., Lauga, E. & Zenit, R. 2019 Viscoelastic propulsion of a rotating dumbbell. Microfluid. Nanofluid. 23 (9), 1–7.Google Scholar
Putz, V.B. & Dunkel, J. 2010 Low Reynolds number hydrodynamics of asymmetric, oscillating dumbbell pairs. Eur. Phys. J. Spec. Top. 187 (1), 135–144.10.1140/epjst/e2010-01278-yCrossRefGoogle Scholar
Qi, K., Annepu, H., Gompper, G. & Winker, R.G. 2020 Rheotaxis of spheroidal squirmers in microchannel flow: Interplay of shape, hydrodynamics, active stress, and thermal fluctuations. Phys. Rev. Res. 2 (3), 033275.10.1103/PhysRevResearch.2.033275CrossRefGoogle Scholar
Qiu, J., Mousavi, N., Gustavsson, K., Xu, C., Mehlig, B. & Zhao, L. 2021 Navigation of micro-swimmers in steady flow: the importance of symmetries. J. Fluid Mech. 932, A10.10.1017/jfm.2021.978CrossRefGoogle Scholar
Qiu, J., Mousavi, N., Zhao, L. & Gustavsson, K. 2022 Active gyrotactic stability of microswimmers using hydromechanical signals. Phys. Rev. Fluids 7 (1), 014311.10.1103/PhysRevFluids.7.014311CrossRefGoogle Scholar
Raza, MdR., George, J.E., Kumari, S., Mitra, M.K. & Paul, D. 2023 Anomalous diffusion of E. Coli under microfluidic confinement and chemical gradient. Soft Matt. 19 (34), 6446–6457.10.1039/D3SM00286ACrossRefGoogle ScholarPubMed
Samatas, S. & Lintuvuori, J.S. 2023 Hydrodynamic synchronization of chiral microswimmers. Phys. Rev. Lett. 130 (2), 024001.10.1103/PhysRevLett.130.024001CrossRefGoogle ScholarPubMed
Sankaewtong, K., Molina, J.J., Turner, M.S. & Yamamoto, R. 2023 Learning to swim efficiently in a nonuniform flow field. Phys. Rev. E 107 (6), 065102.10.1103/PhysRevE.107.065102CrossRefGoogle Scholar
Sankaewtong, K., Molina, J.J. & Yamamoto, R. 2024 Efficient navigation of cargo-towing microswimmer in non-uniform flow fields. Phys. Rev. Res. 6 (3), 033305.10.1103/PhysRevResearch.6.033305CrossRefGoogle Scholar
Sankaewtong, K., Molina, J.J. & Yamamoto, R. 2024 Autonomous navigation of smart microswimmers in non-uniform flow fields. Phys. Fluids 36 (4), 041902.10.1063/5.0193113CrossRefGoogle Scholar
Seymour, J.R., Brumley, D.R., Stocker, R. & Raina, J.-B. 2024 Swimming towards each other: the role of chemotaxis in bacterial interactions. Trends Microbiol. 32 (7), 640–649.10.1016/j.tim.2023.12.008CrossRefGoogle ScholarPubMed
Soto, F., Wang, J., Ahmed, R. & Demirci, U. 2020 Medical micro/nanorobots in precision medicine. Adv. Sci. 7 (21), 2002203.10.1002/advs.202002203CrossRefGoogle ScholarPubMed
Sukhov, A., Ziegler, S., Xie, Q., Trosman, O., Pande, J., Grosjean, G., Hubert, M., Vandewalle, N., Smith, A.-S. & Harting, J. 2019 Optimal motion of triangular magnetocapillary swimmers. J. Chem. Phys. 151 (12), 124707.10.1063/1.5116860CrossRefGoogle ScholarPubMed
Théry, A., Maaß, C.C. & Lauga, E. 2023 Hydrodynamic interactions between squirmers near walls: far-field dynamics and near-field cluster stability. R. Soc. Open Sci. 10 (6), 230223.10.1098/rsos.230223CrossRefGoogle ScholarPubMed
Torres, B.O., Pradeep, Shravan, Ran, R., Jerolmack, D. & Arratia, P.E. 2024 Sedimentation dynamics of passive particles in dilute bacterial suspensions: emergence of bioconvection. J. Fluid Mech. 988, A9.10.1017/jfm.2024.437CrossRefGoogle Scholar
Van Wolferen, M., Orell, A. & Albers, S.-V. 2018 Archaeal biofilm formation. Nat. Rev. Microbiol. 16 (11), 699–713.10.1038/s41579-018-0058-4CrossRefGoogle ScholarPubMed
Wadhwa, N. & Berg, H.C. 2021 Bacterial motility: machinery and mechanisms. Nat. Rev. Microbiol. 20 (3), 1–13.Google ScholarPubMed
Wang, W., Duan, W., Ahmed, S., Sen, A. & Mallouk, T.E. 2015 From one to many: dynamic assembly and collective behavior of self-propelled colloidal motors. Acc. Chem. Res. 48 (7), 1938–1946.10.1021/acs.accounts.5b00025CrossRefGoogle ScholarPubMed
Winkler, R.G. & Gompper, G. 2020 The physics of active polymers and filaments. J. Chem. Phys. 153 (4), 040901.10.1063/5.0011466CrossRefGoogle ScholarPubMed
Wu, K.-T., Hsiao, Y.-T. & Woon, W.-Y. 2018 Entrapment of pusher and puller bacteria near a solid surface. Phys. Rev. E 98 (5), 052407.10.1103/PhysRevE.98.052407CrossRefGoogle Scholar
Yamamoto, T. & Sano, M. 2019 Hydrodynamic rotlet dipole driven by spinning chiral liquid crystal droplets. Phys. Rev. E 99 (2), 022704.10.1103/PhysRevE.99.022704CrossRefGoogle ScholarPubMed
Yan, X., et al. 2017 Multifunctional biohybrid magnetite microrobots for imaging-guided therapy. Sci. Robot. 2 (12), eaaq1155.10.1126/scirobotics.aaq1155CrossRefGoogle ScholarPubMed
Zhang, H., Li, Z., Gao, C., Fan, X., Pang, Y., Li, T., Wu, Z., Xie, H. & He, Q. 2021 Dual-responsive biohybrid neutrobots for active target delivery. Sci. Robot. 6 (52), eaaz9519.10.1126/scirobotics.aaz9519CrossRefGoogle ScholarPubMed
Zhou, Z., Wu, W., Wu, S., Jia, K. & Tsui, P.-H. 2017 Empirical mode decomposition of ultrasound imaging for gain-independent measurement on tissue echogenicity: a feasibility study. Appl. Sci. 7 (4), 324.10.3390/app7040324CrossRefGoogle Scholar
Ziegler, S., Hubert, M., Vandewalle, N., Harting, J. & Smith, A.-S. 2019 A general perturbative approach for bead-based microswimmers reveals rich self-propulsion phenomena. New J. Phys. 21 (11), 113017.10.1088/1367-2630/ab4fc2CrossRefGoogle Scholar