Hostname: page-component-5b777bbd6c-j65dx Total loading time: 0 Render date: 2025-06-18T11:16:20.970Z Has data issue: false hasContentIssue false
  • English
  • Français

Centrifugal convection with oscillating rotating velocity

Published online by Cambridge University Press:  15 May 2025

Jun Zhong Open the ORCID record for Jun Zhong [Opens in a new window] ,
Junyi Li Open the ORCID record for Junyi Li [Opens in a new window] ,
Quan Zhou Open the ORCID record for Quan Zhou [Opens in a new window]  and
Chao Sun Open the ORCID record for Chao Sun [Opens in a new window]
Jun Zhong
Affiliation:
New Cornerstone Science Laboratory, Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, PR China
Junyi Li
Affiliation:
New Cornerstone Science Laboratory, Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, PR China
Quan Zhou*
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Chao Sun*
Affiliation:
New Cornerstone Science Laboratory, Center for Combustion Energy, Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, PR China Department of Engineering Mechanics, School of Aerospace Engineering, Tsinghua University, Beijing 100084, PR China
*
Corresponding authors: Chao Sun, chaosun@tsinghua.edu.cn; Quan Zhou, qzhou@shu.edu.cn
Corresponding authors: Chao Sun, chaosun@tsinghua.edu.cn; Quan Zhou, qzhou@shu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

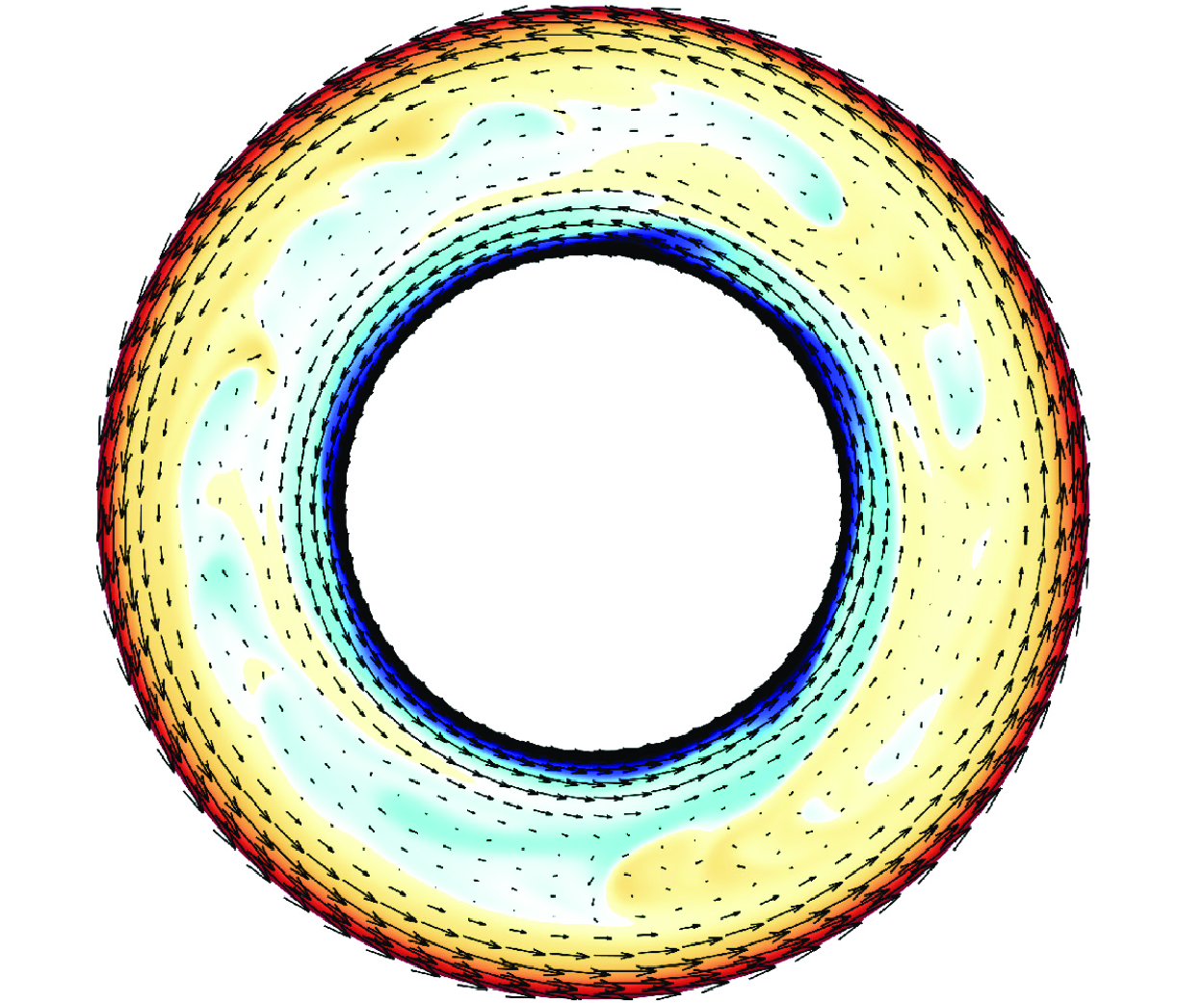
We perform direct numerical simulations of centrifugal convection with an oscillating rotational velocity of small amplitude to study the effects of oscillatory boundary motion. The oscillation period is the main control parameter, with its range corresponding to a Womersley number in the range $1\lt Wo\lt 300$. Oscillating boundaries generate a circumferential shear flow, which significantly inhibits heat transfer, with maximum suppression $87\,\%$ observed in the present parameter space. Through analysis of the background flow, we find that as the oscillation period increases, the increasing penetration depth of the oscillation and weakening local shear strength result in non-monotonic changes in heat transfer. Under high-frequency oscillation, the characteristic length scale of the viscous layer induced by the oscillation is smaller than the convective length scale, and shear manifests primarily as a continuous suppression of the boundary layer. In contrast, under low-frequency oscillation, the shear flow covers the entire region but with weak strength. The suppression effect of such shear flow exhibits periodicity, leading to alternating phases of convection inhibition and convection generation. The present findings explore the physical mechanisms behind the suppression of convective heat transfer by oscillation, and offer a new strategy for controlling convection systems, with potential implications for both fundamental research and industrial applications.

JFM classification

Convection: Plumes/thermals Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1010 , 10 May 2025 , A17
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.CrossRefGoogle Scholar
Anderson, D.L.T. & Gill, A.E. 1975 Spin-up of a stratified ocean, with applications to upwelling. Deep-Sea Res. 22 (9), 583–596.Google Scholar
Barenghi, C.F. & Jones, C.A. 1989 Modulated Taylor–Couette flow. J. Fluid Mech. 208, 127–160.CrossRefGoogle Scholar
Berger, E. & Wille, R. 1972 Periodic flow phenomena. Annu. Rev. Fluid Mech. 4 (1), 313–340.CrossRefGoogle Scholar
Bhadra, A., Shishkina, O. & Zhu, X. 2024 On the boundary-layer asymmetry in two-dimensional annular Rayleigh–Bénard convection subject to radial gravity. J. Fluid Mech. 999, R1.CrossRefGoogle Scholar
Bhadra, A., Shishkina, O. & Zhu, X. 2025 Heat and momentum transfer in Rayleigh–Bénard convection within a two-dimensional annulus under radial gravity. Intl J. Heat Mass Trans. 241, 126703.CrossRefGoogle Scholar
Blass, A., Zhu, X., Verzicco, R., Lohse, D. & Stevens, R.J.A.M. 2020 Flow organization and heat transfer in turbulent wall sheared thermal convection. J. Fluid Mech. 897, A22.CrossRefGoogle ScholarPubMed
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E: Soft Matt. 35 (7), 58.CrossRefGoogle ScholarPubMed
Davis, S.H. 1976 The stability of time-periodic flows. Annu. Rev. Fluid Mech. 8 (1), 57–74.CrossRefGoogle Scholar
Ecke, R.E. & Shishkina, O. 2023 Turbulent rotating Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 55, 603–638.CrossRefGoogle Scholar
Goluskin, D., Johnston, H., Flierl, G.R. & Spiegel, E.A. 2014 Convectively driven shear and decreased heat flux. J. Fluid Mech. 759, 360–385.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Guo, X.-L., Wu, J.-Z., Wang, B.-F., Zhou, Q. & Chong, K.L. 2023 Flow structure transition in thermal vibrational convection. J. Fluid Mech. 974, A29.CrossRefGoogle Scholar
He, S. & Jackson, J.D. 2009 An experimental study of pulsating turbulent flow in a pipe. Eur. J. Mech. B/Fluid 28 (2), 309–320.CrossRefGoogle Scholar
Jiang, H., Wang, D., Liu, S. & Sun, C. 2022 Experimental evidence for the existence of the ultimate regime in rapidly rotating turbulent thermal convection. Phys. Rev. Lett. 129 (20), 204502.CrossRefGoogle ScholarPubMed
Jiang, H., Zhu, X., Mathai, V., Verzicco, R., Lohse, D. & Sun, C. 2018 Controlling heat transport and flow structures in thermal turbulence using ratchet surfaces. Phys. Rev. Lett. 120 (4), 044501.CrossRefGoogle ScholarPubMed
Jiang, H., Zhu, X., Wang, D., Huisman, S.G. & Sun, C. 2020 Supergravitational turbulent thermal convection. Sci. Adv. 6 (40), eabb8676.CrossRefGoogle ScholarPubMed
Jin, X.-L. & Xia, K.-Q. 2008 An experimental study of kicked thermal turbulence. J. Fluid Mech. 606, 133–151.CrossRefGoogle Scholar
Liu, S., Jiang, L., Chong, K.L., Zhu, X., Wan, Z.-H., Verzicco, R., Stevens, R.J.A.M., Lohse, D. & Sun, C. 2020 From Rayleigh–Bénard convection to porous-media convection: how porosity affects heat transfer and flow structure. J. Fluid Mech. 895, A18.CrossRefGoogle Scholar
Liu, Z., Jia, P., Li, M. & Zhong, Z. 2023 Heat transfer modulation in Rayleigh–Bénard convection by an oscillatory bottom plate. Phys. Fluids 35, (3).Google Scholar
Lohse, D. & Shishkina, O. 2023 Ultimate turbulent thermal convection. Phys. Today 76 (11), 26–32.CrossRefGoogle Scholar
Lohse, D. & Shishkina, O. 2024 Ultimate Rayleigh–Bénard turbulence. Rev. Mod. Phys. 96, 035001.CrossRefGoogle Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42 (1), 335–364.CrossRefGoogle Scholar
Niemela, J.J., Skrbek, L., Sreenivasan, K.R. & Donnelly, R.J. 2001 The wind in confined thermal convection. J. Fluid Mech. 449, 169–178.CrossRefGoogle Scholar
Ostilla, R., Stevens, R.J.A.M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.CrossRefGoogle Scholar
Owen, J.M. & Tang, H. 2015 Theoretical model of buoyancy-induced flow in rotating cavities. J. Turbomach. 137 (11), 111005.CrossRefGoogle Scholar
van der Poel, E.P., Ostilla-Mónico, R., Donners, J. & Verzicco, R. 2015 A pencil distributed finite difference code for strongly turbulent wall-bounded flows. Comput. Fluids 116, 10–16.CrossRefGoogle Scholar
Scagliarini, A., Gylfason, Á. & Toschi, F. 2014 Heat-flux scaling in turbulent Rayleigh–Bénard convection with an imposed longitudinal wind. Phys. Rev. E 89 (4), 043012.CrossRefGoogle ScholarPubMed
Schumacher, J. & Sreenivasan, K.R. 2020 Colloquium: unusual dynamics of convection in the sun. Rev. Mod. Phys. 92, 041001.CrossRefGoogle Scholar
Song, J., Shishkina, O. & Zhu, X. 2024 Scaling regimes in rapidly rotating thermal convection at extreme Rayleigh numbers. J. Fluid Mech. 984, A45.CrossRefGoogle Scholar
Song, Y. & Rau, M.J. 2020 Viscous fluid flow inside an oscillating cylinder and its extension to Stokes’ second problem. Phys. Fluids 32 (4), 043601.CrossRefGoogle Scholar
Sterl, S., Li, H.-M. & Zhong, J.-Q. 2016 Dynamical and statistical phenomena of circulation and heat transfer in periodically forced rotating turbulent Rayleigh–Bénard convection. Phys. Rev. Fluids 1 (8), 084401.CrossRefGoogle Scholar
Telford, W.M. 1967 Graphical representation of mantle convection. Nature 216 (5111), 143–146.CrossRefGoogle Scholar
Verschoof, R.A., Te Nijenhuis, A.K., Huisman, S.G., Sun, C. & Lohse, D. 2018 Periodically driven Taylor–Couette turbulence. J. Fluid Mech. 846, 834–845.CrossRefGoogle Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123 (2), 402–414.CrossRefGoogle Scholar
Walsh, T.J. & Donnelly, R.J. 1988 Taylor–Couette flow with periodically corotated and counterrotated cylinders. Phys. Rev. Lett. 60 (8), 700–703.CrossRefGoogle ScholarPubMed
Wang, B.-F., Zhou, Q. & Sun, C. 2020 Vibration-induced boundary-layer destabilization achieves massive heat-transport enhancement. Sci. Adv. 6 (21), eaaz8239.CrossRefGoogle ScholarPubMed
Wang, D., Liu, J., Lai, R. & Sun, C. 2024 Temperature fluctuations and heat transport in partitioned supergravitational thermal turbulence. Acta Mech. Sin. 40 (6), 723405.CrossRefGoogle Scholar
Wang, D., Jiang, H., Liu, S., Zhu, X. & Sun, C. 2022 a Effects of radius ratio on annular centrifugal Rayleigh–Bénard convection. J. Fluid Mech. 930, A19.CrossRefGoogle Scholar
Wang, D., Liu, J., Zhou, Q. & Sun, C. 2022 b Statistics of temperature and velocity fluctuations in supergravitational convective turbulence. Acta Mech. Sin. 39 (4), 122387.CrossRefGoogle Scholar
Womersley, J.R. 1955 Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 127 (3), 553–563.CrossRefGoogle ScholarPubMed
Wu, J.-Z., Wang, B.-F., Chong, K.L., Dong, Y.-H., Sun, C. & Zhou, Q. 2022 Vibration-induced anti-gravity tames thermal turbulence at high Rayleigh numbers. J. Fluid Mech. 951, A13.CrossRefGoogle Scholar
Yan, M., Tobias, S.M. & Calkins, M.A. 2021 Scaling behaviour of small-scale dynamos driven by Rayleigh–Bénard convection. J. Fluid Mech. 915, A15.CrossRefGoogle Scholar
Yang, R., Chong, K.L., Wang, Q., Verzicco, R., Shishkina, O. & Lohse, D. 2020 Periodically modulated thermal convection. Phys. Rev. Lett. 125 (15), 154502.CrossRefGoogle ScholarPubMed
Yao, Z., Emran, M.S., Teimurazov, A. & Shishkina, O. 2025 Direct numerical simulations of centrifugal convection: from gravitational to centrifugal buoyancy dominance. Intl J. Heat Mass Transfer 236, 126314.CrossRefGoogle Scholar
Yeh, H. 2023 Geophysical fluid dynamics in the hypergravity field. Acta Mech. Sin. 40 (2), 723296.CrossRefGoogle Scholar
Zhong, J., Li, J. & Sun, C. 2024 Effect of radius ratio on the sheared annular centrifugal turbulent convection. J. Fluid Mech. 992, A16.CrossRefGoogle Scholar
Zhong, J., Wang, D. & Sun, C. 2023 From sheared annular centrifugal Rayleigh–Bénard convection to radially heated Taylor–Couette flow: exploring the impact of buoyancy and shear on heat transfer and flow structure. J. Fluid Mech. 972, A29.CrossRefGoogle Scholar
Zhong, J.-Q., Stevens, R.J.A.M., Clercx, H.J.H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102 (4), 044502.CrossRefGoogle ScholarPubMed
Zhu, X., et al. 2018 AFiD-GPU: a versatile Navier–Stokes solver for wall-bounded turbulent flows on GPU clusters. Comput. Phys. Commun. 229, 199–210.CrossRefGoogle Scholar