Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bai, H. L.
Kevin
Hutchins, N.
and
Monty, J. P.
2018.
Turbulence modifications in a turbulent boundary layer over a rough wall with spanwise-alternating roughness strips.
Physics of Fluids,
Vol. 30,
Issue. 5,
Chan, L.
MacDonald, M.
Chung, D.
Hutchins, N.
and
Ooi, A.
2018.
Secondary motion in turbulent pipe flow with three-dimensional roughness.
Journal of Fluid Mechanics,
Vol. 854,
Issue. ,
p.
5.
Anderson, William
Yang, Jianzhi
Shrestha, Kalyan
and
Awasthi, Ankit
2018.
Turbulent secondary flows in wall turbulence: vortex forcing, scaling arguments, and similarity solution.
Environmental Fluid Mechanics,
Vol. 18,
Issue. 6,
p.
1351.
Chung, D.
Monty, J. P.
and
Hutchins, N.
2018.
Similarity and structure of wall turbulence with lateral wall shear stress variations.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
p.
591.
Ferreira, M. Aguiar
Rodriguez-Lopez, E.
and
Ganapathisubramani, B.
2018.
An alternative floating element design for skin-friction measurement of turbulent wall flows.
Experiments in Fluids,
Vol. 59,
Issue. 10,
Awasthi, Ankit
and
Anderson, William
2018.
Numerical study of turbulent channel flow perturbed by spanwise topographic heterogeneity: Amplitude and frequency modulation within low- and high-momentum pathways.
Physical Review Fluids,
Vol. 3,
Issue. 4,
Ni, Weidan
Lu, Lipeng
Fang, Jian
Moulinec, Charles
Emerson, David R.
and
Yao, Yufeng
2019.
Flow separation control over a rounded ramp with spanwise alternating wall actuation.
Physics of Fluids,
Vol. 31,
Issue. 1,
Vanderwel, C.
Stroh, A.
Kriegseis, J.
Frohnapfel, B.
and
Ganapathisubramani, B.
2019.
The instantaneous structure of secondary flows in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 862,
Issue. ,
p.
845.
Meyers, Johan
Ganapathisubramani, Bharathram
and
Cal, Raúl Bayoán
2019.
On the decay of dispersive motions in the outer region of rough-wall boundary layers.
Journal of Fluid Mechanics,
Vol. 862,
Issue. ,
Anderson, W.
2019.
Non-periodic phase-space trajectories of roughness-driven secondary flows in high- boundary layers and channels.
Journal of Fluid Mechanics,
Vol. 869,
Issue. ,
p.
27.
Xu, Fang
Zhong, Shan
and
Zhang, Shanying
2019.
Statistical analysis of vortical structures in turbulent boundary layer over directional grooved surface pattern with spanwise heterogeneity.
Physics of Fluids,
Vol. 31,
Issue. 8,
Zampiron, Andrea
Nikora, Vladimir
Cameron, Stuart
Patella, Wada
Valentini, Isacco
and
Stewart, Mark
2020.
Effects of Streamwise Ridges on Hydraulic Resistance in Open-Channel Flows.
Journal of Hydraulic Engineering,
Vol. 146,
Issue. 1,
Xie, Michael X
Chung, Daniel
and
Hutchins, Nicholas
2020.
Turbulent flow over spanwise-varying roughness in a minimal streamwise channel.
Journal of Physics: Conference Series,
Vol. 1522,
Issue. 1,
p.
012018.
Xu, Fang
Zhong, Shan
and
Zhang, Shanying
2020.
Experimental study on secondary flow in turbulent boundary layer over spanwise heterogeneous microgrooves.
Physics of Fluids,
Vol. 32,
Issue. 3,
Yao, Chanjuan
Li, Botong
Si, Xinhui
and
Meng, Yahui
2020.
On fluid flow and heat transfer of turbulent boundary layer of pseudoplastic fluids on a semi-infinite plate.
Physics of Fluids,
Vol. 32,
Issue. 7,
Stroh, A.
Schäfer, K.
Frohnapfel, B.
and
Forooghi, P.
2020.
Rearrangement of secondary flow over spanwise heterogeneous roughness.
Journal of Fluid Mechanics,
Vol. 885,
Issue. ,
Stroh, A.
Schäfer, K.
Forooghi, P.
and
Frohnapfel, B.
2020.
Secondary flow and heat transfer in turbulent flow over streamwise ridges.
International Journal of Heat and Fluid Flow,
Vol. 81,
Issue. ,
p.
108518.
Wangsawijaya, Dea D.
Baidya, Rio
Chung, Daniel
Marusic, Ivan
and
Hutchins, Nicholas
2020.
The effect of spanwise wavelength of surface heterogeneity on turbulent secondary flows.
Journal of Fluid Mechanics,
Vol. 894,
Issue. ,
Bakhuis, Dennis
Ezeta, Rodrigo
Berghout, Pieter
Bullee, Pim A.
Tai, Dominic
Chung, Daniel
Verzicco, Roberto
Lohse, Detlef
Huisman, Sander G.
and
Sun, Chao
2020.
Controlling secondary flow in Taylor–Couette turbulence through spanwise-varying roughness.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Zampiron, A.
Cameron, S.
and
Nikora, V.
2020.
Secondary currents and very-large-scale motions in open-channel flow over streamwise ridges.
Journal of Fluid Mechanics,
Vol. 887,
Issue. ,
 $S$ is comparable to the boundary-layer thickness (
$S$ is comparable to the boundary-layer thickness (  $S/\unicode[STIX]{x1D6FF}=O(1)$ ). Single-point velocity measurements alongside direct skin-friction measurements are used to examine the validity of Townsend’s similarity hypothesis. The skin-friction coefficients reveal that the drag of the heterogeneous surface increased up to 35 % compared to a smooth wall, while velocity measurements reveal the existence of a log layer but with a zero-plane displacement and a roughness function that vary across the spanwise direction. Lack of collapse in the outer region of the mean velocity and variance profiles is attributed to the secondary flows induced by the heterogeneous surfaces. Additionally, the lack of similarity also extends to the spectra across all scales in the near-wall region with a gradual collapse at small wavelengths for increasing
$S/\unicode[STIX]{x1D6FF}=O(1)$ ). Single-point velocity measurements alongside direct skin-friction measurements are used to examine the validity of Townsend’s similarity hypothesis. The skin-friction coefficients reveal that the drag of the heterogeneous surface increased up to 35 % compared to a smooth wall, while velocity measurements reveal the existence of a log layer but with a zero-plane displacement and a roughness function that vary across the spanwise direction. Lack of collapse in the outer region of the mean velocity and variance profiles is attributed to the secondary flows induced by the heterogeneous surfaces. Additionally, the lack of similarity also extends to the spectra across all scales in the near-wall region with a gradual collapse at small wavelengths for increasing 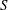 $S$ . This suggests that the effect of surface heterogeneity is not necessarily felt at the smaller scales other than to reorganise their presence through turbulent transport.
$S$ . This suggests that the effect of surface heterogeneity is not necessarily felt at the smaller scales other than to reorganise their presence through turbulent transport.

