Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ali, Naseem
Viggiano, Bianca
Tutkun, Murat
and
Cal, Raúl Bayoán
2020.
Cluster-based reduced-order descriptions of two phase flows.
Chemical Engineering Science,
Vol. 222,
Issue. ,
p.
115660.
Lennie, Matthew
Steenbuck, Johannes
Noack, Bernd R.
and
Paschereit, Christian Oliver
2020.
Cartographing dynamic stall with machine learning.
Wind Energy Science,
Vol. 5,
Issue. 2,
p.
819.
Zhou, Yu
Fan, Dewei
Zhang, Bingfu
Li, Ruiying
and
Noack, Bernd R.
2020.
Artificial intelligence control of a turbulent jet.
Journal of Fluid Mechanics,
Vol. 897,
Issue. ,
Taira, Kunihiko
Hemati, Maziar S.
Brunton, Steven L.
Sun, Yiyang
Duraisamy, Karthik
Bagheri, Shervin
Dawson, Scott T. M.
and
Yeh, Chi-An
2020.
Modal Analysis of Fluid Flows: Applications and Outlook.
AIAA Journal,
Vol. 58,
Issue. 3,
p.
998.
Cheng, M.
Fang, F.
Pain, C.C.
and
Navon, I.M.
2020.
Data-driven modelling of nonlinear spatio-temporal fluid flows using a deep convolutional generative adversarial network.
Computer Methods in Applied Mechanics and Engineering,
Vol. 365,
Issue. ,
p.
113000.
Agostini, Lionel
2020.
Exploration and prediction of fluid dynamical systems using auto-encoder technology.
Physics of Fluids,
Vol. 32,
Issue. 6,
Bieker, Katharina
Peitz, Sebastian
Brunton, Steven L.
Kutz, J. Nathan
and
Dellnitz, Michael
2020.
Deep model predictive flow control with limited sensor data and online learning.
Theoretical and Computational Fluid Dynamics,
Vol. 34,
Issue. 4,
p.
577.
Asztalos, Katherine J.
Dawson, Scott T.
and
Williams, David R.
2020.
The Sensitivity of Leading-Edge Momentum Injection Response to Instantaneous Flow State for an Airfoil in Deep Stall.
Barwey, Shivam
Raman, Venkatramanan
and
Steinberg, Adam M.
2020.
Data-Driven Reduction and Decomposition via Time-Axis Clustering.
Boutselis, George I.
Evans, Ethan N.
Pereira, Marcus A.
and
Theodorou, Evangelos A.
2021.
Leveraging Stochasticity for Open Loop and Model Predictive Control of Spatio-Temporal Systems.
Entropy,
Vol. 23,
Issue. 8,
p.
941.
Li, Hao
Fernex, Daniel
Semaan, Richard
Tan, Jianguo
Morzyński, Marek
and
Noack, Bernd R.
2021.
Cluster-based network model.
Journal of Fluid Mechanics,
Vol. 906,
Issue. ,
Asztalos, Katherine J.
Dawson, Scott T.
and
Williams, David R.
2021.
Modeling the Dynamics of Actuation on an Airfoil at Post-Stall Angles of Attack.
Iacobello, G.
Ridolfi, L.
and
Scarsoglio, S.
2021.
A review on turbulent and vortical flow analyses via complex networks.
Physica A: Statistical Mechanics and its Applications,
Vol. 563,
Issue. ,
p.
125476.
Blanchard, Antoine B.
Cornejo Maceda, Guy Y.
Fan, Dewei
Li, Yiqing
Zhou, Yu
Noack, Bernd R.
and
Sapsis, Themistoklis P.
2021.
Bayesian optimization for active flow control.
Acta Mechanica Sinica,
Vol. 37,
Issue. 12,
p.
1786.
Cornejo Maceda, Guy Y.
Li, Yiqing
Lusseyran, François
Morzyński, Marek
and
Noack, Bernd R.
2021.
Stabilization of the fluidic pinball with gradient-enriched machine learning control.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
Kou, Jiaqing
and
Zhang, Weiwei
2021.
Data-driven modeling for unsteady aerodynamics and aeroelasticity.
Progress in Aerospace Sciences,
Vol. 125,
Issue. ,
p.
100725.
Nair, Aditya G.
Taira, Kunihiko
Brunton, Bingni W.
and
Brunton, Steven L.
2021.
Phase-based control of periodic flows.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
Foroozan, F.
Guerrero, V.
Ianiro, A.
and
Discetti, S.
2021.
Unsupervised modelling of a transitional boundary layer.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Asztalos, Katherine J.
Dawson, Scott T. M.
and
Williams, David R.
2021.
Modeling the Flow State Sensitivity of Actuation Response on a Stalled Airfoil.
AIAA Journal,
p.
1.
Wu, Meng
Payshanbiev, Adim
Zhao, Qing
and
Yang, Wenzong
2021.
Nonlinear optimization generating the Tomb Mural Blocks by GANS.
Applied Mathematics and Nonlinear Sciences,
Vol. 6,
Issue. 1,
p.
43.
 $O(10)$ iterations. The objective of the present work is not necessarily to suppress flow separation but to minimize the desired cost function to achieve enhanced aerodynamic performance. The present approach is applied to the control of two- and three-dimensional separated flows over a NACA 0012 airfoil in large-eddy simulations at an angle of attack of
$O(10)$ iterations. The objective of the present work is not necessarily to suppress flow separation but to minimize the desired cost function to achieve enhanced aerodynamic performance. The present approach is applied to the control of two- and three-dimensional separated flows over a NACA 0012 airfoil in large-eddy simulations at an angle of attack of 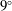 $9^{\circ }$, Reynolds number
$9^{\circ }$, Reynolds number 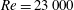 $Re=23\,000$ and free-stream Mach number
$Re=23\,000$ and free-stream Mach number 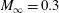 $M_{\infty }=0.3$. The optimized control laws avoid the intermittent occurrence of long-period shedding associated with high-drag clusters, thus lowering the mean drag. The present work aims to address some of the challenges associated with feedback control design for turbulent separated flows at moderate Reynolds number.
$M_{\infty }=0.3$. The optimized control laws avoid the intermittent occurrence of long-period shedding associated with high-drag clusters, thus lowering the mean drag. The present work aims to address some of the challenges associated with feedback control design for turbulent separated flows at moderate Reynolds number.
