Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-23T11:01:16.357Z Has data issue: false hasContentIssue false
  • English
  • Français

Computations of fully nonlinear hydroelastic solitary waves on deep water

Published online by Cambridge University Press:  17 October 2012

Philippe Guyenne  and
Emilian I. Pǎrǎu
Philippe Guyenne
Affiliation:
Department of Mathematical Sciences, University of Delaware, DE 19716, USA
Emilian I. Pǎrǎu*
Affiliation:
School of Mathematics, University of East Anglia, Norwich NR4 7TJ, UK
*
†Email address for correspondence: e.parau@uea.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the two-dimensional problem of nonlinear gravity waves travelling at the interface between a thin ice sheet and an ideal fluid of infinite depth. The ice-sheet model is based on the special Cosserat theory of hyperelastic shells satisfying Kirchhoff’s hypothesis, which yields a conservative and nonlinear expression for the bending force. A Hamiltonian formulation for this hydroelastic problem is proposed in terms of quantities evaluated at the fluid–ice interface. For small-amplitude waves, a nonlinear Schrödinger equation is derived and its analysis shows that no solitary wavepackets exist in this case. For larger amplitudes, both forced and free steady waves are computed by direct numerical simulations using a boundary-integral method. In the unforced case, solitary waves of depression as well as of elevation are found, including overhanging waves with a bubble-shaped profile for wave speeds $c$ much lower than the minimum phase speed 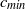${c}_{\mathit{min}} $. It is also shown that the energy of depression solitary waves has a minimum at a wave speed 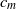${c}_{m} $ slightly less than ${c}_{\mathit{min}} $, which suggests that such waves are stable for 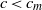$c\lt {c}_{m} $ and unstable for 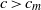$c\gt {c}_{m} $. This observation is verified by time-dependent computations using a high-order spectral method. These computations also indicate that solitary waves of elevation are likely to be unstable.

JFM classification

Waves/Free-surface Flows: Elastic waves Waves/Free-surface Flows: Solitary waves Mathematical Foundations: Hamiltonian theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 713 , 25 December 2012 , pp. 307 - 329
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akers, B. & Milewski, P. A. 2010 Dynamics of three-dimensional gravity–capillary solitary waves. SIAM J. Appl. Maths 70, 2373–2389.Google Scholar
Akylas, T. R. 1993 Envelope solitons with stationary crests. Phys. Fluids A 5, 789–791.Google Scholar
Akylas, T. R. & Cho, Y. 2008 On the stability of lumps and wave collapse in water waves. Phil. Trans. R. Soc. Lond. A 366, 2761–2774.Google ScholarPubMed
Blyth, M. G., Părău, E. I. & Vanden-Broeck, J.-M. 2011 Hydroelastic waves on fluid sheets. J. Fluid Mech. 689, 541–551.CrossRefGoogle Scholar
Bonnefoy, F., Meylan, M. H. & Ferrant, P. 2009 Nonlinear higher-order spectral solution for a two-dimensional moving load on ice. J. Fluid Mech. 621, 215–242.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1987 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Craig, W., Guyenne, P., Nicholls, D. P. & Sulem, C. 2005 Hamiltonian long-wave expansions for water waves over a rough bottom. Proc. R. Soc. Lond. A 461, 839–873.Google Scholar
Craig, W., Guyenne, P. & Sulem, C. 2010 A Hamiltonian approach to nonlinear modulation of surface water waves. Wave Motion 47, 552–563.Google Scholar
Craig, W., Guyenne, P. & Sulem, C. 2012 Hamiltonian higher-order nonlinear Schrödinger equations for broader-banded waves on deep water. Eur. J. Mech. B/Fluids 32, 22–31.CrossRefGoogle Scholar
Craig, W., Schanz, U. & Sulem, C. 1997 The modulational regime of three-dimensional water waves and the Davey–Stewartson system. Ann. Inst. H. Poincaré (C) Nonlin. Anal. 14, 615–667.Google Scholar
Craig, W. & Sulem, C. 1993 Numerical simulation of gravity waves. J. Comput. Phys. 108, 73–83.Google Scholar
Crapper, G. D. 1957 An exact solution for progressive capillary waves of arbitrary amplitude. J. Fluid Mech. 2, 532–540.Google Scholar
Forbes, L. K. 1986 Surface-waves of large amplitude beneath an elastic sheet. Part 1. High-order solutions. J. Fluid Mech. 169, 409–428.Google Scholar
Forbes, L. K. 1988 Surface-waves of large amplitude beneath an elastic sheet. Part 2. Galerkin solution. J. Fluid Mech. 188, 491–508.Google Scholar
Guyenne, P. & Nicholls, D. P. 2007 A high-order spectral method for nonlinear water waves over moving bottom topography. SIAM J. Sci. Comput. 30, 81–101.Google Scholar
Hegarty, G. M. & Squire, V. A. 2008 A boundary-integral method for the interaction of large-amplitude ocean waves with a compliant floating raft such as a sea-ice floe. J. Engng Maths 62, 355–372.Google Scholar
Korobkin, A., Părău, E. I. & Vanden-Broeck, J.-M. 2011 The mathematical challenges and modelling of hydroelasticity. Phil. Trans. R. Soc. Lond. A 369, 2803–2812.Google Scholar
Longuet-Higgins, M. S. 1989 Capillary-gravity waves of solitary type on deep water. J. Fluid Mech. 200, 451–470.CrossRefGoogle Scholar
Marko, J. R. 2003 Observations and analyses of an intense waves-in-ice event in the Sea of Okhotsk. J. Geophys. Res. 108, 3296.Google Scholar
Milewski, P. A., Vanden-Broeck, J.-M. & Wang, Z. 2010 Dynamics of steep two-dimensional gravity–capillary solitary waves. J. Fluid Mech. 664, 466–477.Google Scholar
Milewski, P. A., Vanden-Broeck, J.-M. & Wang, Z. 2011 Hydroelastic solitary waves in deep water. J. Fluid Mech. 679, 628–640.CrossRefGoogle Scholar
Părău, E. & Dias, F. 2002 Nonlinear effects in the response of a floating ice plate to a moving load. J. Fluid Mech. 460, 281–305.Google Scholar
Părău, E. & Vanden-Broeck, J.-M. 2011 Three-dimensional waves beneath an ice sheet due to a steadily moving pressure. Phil. Trans. R. Soc. Lond. A 369, 2973–2988.Google Scholar
Plotnikov, P I & Toland, J. F. 2011 Modelling nonlinear hydroelastic waves. Phil. Trans. R. Soc. Lond. A 369, 2942–2956.Google Scholar
Saffman, P. G. 1985 The superharmonic instability of finite-amplitude water waves. J. Fluid Mech. 159, 169–174.Google Scholar
Squire, V. A., Hosking, R. J., Kerr, A. D. & Langhorne, P. J. 1996 Moving Loads on Ice Plates. Kluwer.Google Scholar
Takizawa, T. 1985 Deflection of a floating sea ice sheet induced by a moving load. Cold Reg. Sci. Technol. 11, 171–180.Google Scholar
Vanden-Broeck, J.-M. 2010 Gravity–Capillary Free-Surface Flows. Cambridge University Press.Google Scholar
Vanden-Broeck, J.-M. & Dias, F. 1992 Gravity–capillary solitary waves in water of infinite depth and related free-surface flows. J. Fluid Mech. 240, 549–557.Google Scholar
Vanden-Broeck, J.-M. & Părău, E. I. 2011 Two-dimensional generalized solitary waves and periodic waves under an ice sheet. Phil. Trans. R. Soc. Lond. A 369, 2957–2972.Google Scholar
Xu, L. & Guyenne, P. 2009 Numerical simulation of three-dimensional nonlinear water waves. J. Comput. Phys. 228, 8446–8466.Google Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9, 190–194.Google Scholar