Hostname: page-component-797576ffbb-k7d4m Total loading time: 0 Render date: 2023-12-02T14:10:58.270Z Has data issue: false Feature Flags: { "corePageComponentGetUserInfoFromSharedSession": true, "coreDisableEcommerce": false, "useRatesEcommerce": true } hasContentIssue false
  • English
  • Français

Critical reflection and abyssal trapping of near-inertial waves on a β-plane

Published online by Cambridge University Press:  28 September 2011

Kraig B. Winters ,
Pascale Bouruet-Aubertot  and
Theo Gerkema
Kraig B. Winters*
Affiliation:
Scripps Institution of Oceanography, Mechanical and Aerospace Engineering, University of California San Diego, La Jolla, CA 92093-0209, USA
Pascale Bouruet-Aubertot
Affiliation:
Laboratoire d’océanographie et du climat: expérimentation et approches numériques, UPMC/CRNS, BP 100, 4 place Jussieu, 75252 Paris CEDEX 05, France
Theo Gerkema
Affiliation:
Royal Netherlands Institute for Sea Research, NL-1790 AB Den Burg (Texel), The Netherlands
*
†Email address for correspondence: kraig@coast.ucsd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider near-inertial waves continuously excited by a localized source and their subsequent radiation and evolution on a two-dimensional 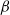-plane. Numerical simulations are used to quantify the wave propagation and the energy flux in a realistically stratified ocean basin. We focus on the dynamics near and poleward of the inertial latitude where the local value of the Coriolis parameter 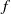matches the forcing frequency 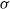, contrasting the behaviour of waves under the traditional approximation (TA), where only the component of the Earth’s rotation aligned with gravity is retained in the dynamics, with that obtained under the non-traditional approach (non-TA) in which the horizontal component of rotation is retained. Under the TA, assuming inviscid linear wave propagation in the WKB limit, all energy radiated from the source eventually propagates toward the equator, with the initially poleward propagation being internally reflected at the inertial latitude. Under the non-TA however, these waves propagate sub-inertially beyond their inertial latitude, exhibiting multiple reflections between internal turning points that lie poleward of the inertial latitude and the bottom. The numerical experiments complement and extend existing theory by relaxing the linearity and WKB approximations, and by illustrating the time development of the steadily forced flow and the spatial patterns of energy flux and flux divergence. The flux divergence of the flow at both the forcing frequency and its first harmonic reveal the spatial patterns of nonlinear energy transfer and highlight the importance of nonlinearity in the vicinity of near-critical bottom reflection at the inertial latitude of the forced waves.

JFM classification

Geophysical and Geological Flows: Ocean processes Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 684 , 10 October 2011 , pp. 111 - 136
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bouruet-Aubertot, P., Koudella, C., Staquet, C. & Winters, K. B. 2001 Particle dispersion and mixing induced by breaking internal gravity waves. Dyn. Atmos. Oceans 33, 95–134.Google Scholar
2. D’Asaro, E. A., Eriksen, C. C., Levine, M. A., Niiler, P., Paulson, C. A. & van Meurs, P. 1995 Upper ocean inertial currents forced by a strong storm. Part I: data and comparisons with linear theory. J. Phys. Oceanogr. 25, 2909–2936.Google Scholar
3. Dauxois, T. & Young, W. R. 1999 Near critical reflection of internal waves. J. Fluid Mech. 390, 271–295.Google Scholar
4. Dintrans, B., Rieutord, M. & Valdettaro, L. 1999 Gravito-inertial waves in a rotating stratified sphere or spherical shell. J. Fluid Mech. 398, 271–297.Google Scholar
5. Durran, D. & Bretherton, C. 2004 Comments on ‘The roles of the horizontal component of the Earth’s angular velocity in nonhydrostatic linear models’. J. Atmos. Sci. 61, 1982–1986.Google Scholar
6. Eriksen, C. C. 1985 Implications of ocean bottom reflection for internal wave spectra and mixing. J. Phys. Oceanogr. 15, 1145–1156.Google Scholar
7. Friedlander, S. & Siegmann, W. L. 1982 Internal waves in a rotating stratified fluid in an arbitrary gravitational field. Geophys. Astrophys. Fluid Dyn. 19, 267–291.Google Scholar
8. Gerkema, T. & Exarchou, E. 2008 Internal-wave properties in weakly stratified layers. J. Mar. Res. 66, 617–644.Google Scholar
9. Gerkema, T. & Shrira, V. I. 2005a Near-inertial waves on the ‘nontraditional’ -plane. J Geophys. Res. 110, C01003.Google Scholar
10. Gerkema, T. & Shrira, V. I. 2005b Near-inertial waves in the ocean: beyond the ‘traditional approximation’. J. Fluid Mech. 529, 195–219.Google Scholar
11. Gerkema, T., Staquet, C. & Bouruet-Aubertot, P. 2006 Decay of semi-diurnal internal-tide beams due to subharmonic resonance. Geophys. Res. Lett. 33, L08604.Google Scholar
12. Gerkema, T., Zimmerman, J. T. F., Maas, L. R. M. & van Haren, H. 2008 Geophysical and astrophysical fluid dynamics beyond the traditional approximation. Rev. Geophys. 46, RG2004.Google Scholar
13. Gilbert, D. & Garrett, C. 1989 Implications for ocean mixing of internal wave scattering off irregular topography. J. Phys. Oceanogr. 19, 1716–1729.Google Scholar
14. Grimshaw, R. H. J. 1975 A note on the -plane approximation. Tellus 27, 351–357.Google Scholar
15. Harlander, U. & Maas, L. R. M. 2006 Characteristics and energy rays of equatorially trapped, zonally symmetric internal waves. Meteorol. Z. 15 (4), 439–450.Google Scholar
16. Hazewinkel, J. & Winters, K. B. 2011 PSI of the internal tide on a -plane: flux divergence and near-inertial wave propagation. J. Phys Oceanogr. (accepted).Google Scholar
17. Holliday, D. & Mcintyre, M. E. 1981 On potential energy density in an incompressible, stratified fluid. J. Fluid Mech. 107, 221–225.Google Scholar
18. Ivey, G. N. & Nokes, R. I. 1989 Vertical mixing due to the breaking of critical internal waves on sloping boundaries. J. Fluid Mech. 204, 479–500.Google Scholar
19. Ivey, G. N., Winters, K. B. & De Silva, I. P. D. 2000 Turbulent mixing in a sloping benthic boundary layer energised by internal waves. J. Fluid Mech. 418, 59–76.Google Scholar
20. Kasahara, A. 2003 The roles of the horizontal component of the Earth’s angular velocity in nonhydrostatic linear models. J. Atmos. Sci. 60, 1085–1095.Google Scholar
21. Kasahara, A. 2004 Reply to Comments on ‘The roles of the horizontal component of the Earth’s angular velocity in nonhydrostatic linear models’. J. Atmos. Sci. 61, 1987–1991.Google Scholar
22. Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.Google Scholar
23. Maas, L. R. M. 2001 Wave focusing and ensuing mean flow due to symmetry breaking in rotating fluids. J. Fluid Mech. 437, 13–28.Google Scholar
24. Maas, L. R. M. 2005 Wave attractors: linear yet nonlinear. Intl J. Bifurcations Chaos 15 (9), 2757–2782.Google Scholar
25. MacKinnon, J. A. & Winters, K. B. 2005 Subtropical catastrophe: significant loss of low-mode tidal energy at 28.9∘ . Geophys. Res. Lett. 32, L15605.Google Scholar
26. McComas, C. H. & Bretherton, F. P. 1977 Resonant interaction of oceanic internal waves: the dynamic balance of internal waves. J. Geophys. Res. 82, 1397–1412.Google Scholar
27. Mercier, M. J., Garnier, N. B. & Dauxois, T. 2008 Reflection and diffraction of internal waves analyzed with the Hilbert transform. Phys. Fluids 20, 086601.Google Scholar
28. Slinn, D. N. & Riley, J. J. 1998 Turbulent dynamics of a critically reflecting internal gravity wave. Theor. Comput. Fluid Dyn. 11, 281–303.Google Scholar
29. Winters, K. B., MacKinnon, J. A. & Mills, B. 2004 A spectral model for process studies of rotating, density-stratified flows. J. Atmos. Ocean. Technol. 21, 69–94.Google Scholar
30. Veronis, G. 1970 The analogy between rotating and stratified fluids. Annu. Rev. Fluid Mech. 2, 37–66.Google Scholar