Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-19T12:37:48.561Z Has data issue: false hasContentIssue false
  • English
  • Français

Deformation and orientation statistics of neutrally buoyant sub-Kolmogorov ellipsoidal droplets in turbulent Taylor–Couette flow

Published online by Cambridge University Press:  14 November 2016

Vamsi Spandan ,
Detlef Lohse  and
Roberto Verzicco
Vamsi Spandan
Affiliation:
Physics of Fluids, University of Twente, Enschede, PO Box 217, 7500 AE, Netherlands
Detlef Lohse
Affiliation:
Physics of Fluids, University of Twente, Enschede, PO Box 217, 7500 AE, Netherlands Max Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany
Roberto Verzicco*
Affiliation:
Physics of Fluids, University of Twente, Enschede, PO Box 217, 7500 AE, Netherlands Dipartimento di Ingegneria Meccanica, University of Rome ‘Tor Vergata’, Via del Politecnico 1, Rome 00133, Italy
*
†Email address for correspondence: verzicco@uniroma2.it
Get access Rights & Permissions [Opens in a new window]

Abstract

The influence of the underlying flow topology on the shape and size of sub-Kolmogorov droplets dispersed in a turbulent flow is of considerable interest in many industrial and scientific applications. In this work we study the deformation and orientation statistics of sub-Kolmogorov droplets dispersed into a turbulent Taylor–Couette flow. Along with direct numerical simulations (DNS) of the carrier phase and Lagrangian tracking of the dispersed droplets, we solve a phenomenological equation proposed by Maffettone and Minale (J. Non-Newtonian Fluid Mech., vol. 78, 1998, pp. 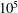227–241) to track the shape evolution and orientation of approximately $10^{5}$ ellipsoidal droplets. By varying the capillary number 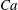$Ca$ and viscosity ratio 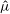$\hat{\unicode[STIX]{x1D707}}$ of the droplets we find that they deform more with increasing capillary number 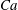$Ca$ and this effect is more pronounced in the boundary layer regions. This indicates that along with an expected capillary number effect there is also a strong correlation between spatial position and degree of deformation of the droplet. Regardless of the capillary number 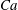$Ca$, the major axis of the ellipsoids tends to align with the streamwise direction and the extensional strain rate eigendirection in the boundary layer region while the distribution is highly isotropic in the bulk due to the strong mixing provided by the large-scale vortical structures. When the viscosity ratio between the droplet and the carrier fluid is increased we find that there is no preferential stretched axis which is due to the increased influence of rotation over stretching and relaxation. Droplets in high viscosity ratio systems are thus less deformed and oblate (disk-like) as compared to highly deformed prolate (cigar-like) droplets in low viscosity ratio systems.

JFM classification

Drops and Bubbles: Drops and Bubbles Multiphase and Particle-laden Flows: Multiphase flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 809 , 25 December 2016 , pp. 480 - 501
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.Google Scholar
Babler, M. U., Biferale, L., Brandt, L., Feudel, U., Guseva, K., Lanotte, A. S., Marchioli, C., Picano, F., Sardina, G. & Soldati, A. 2015 Numerical simulations of aggregate breakup in bounded and unbounded turbulent flows. J. Fluid Mech. 766, 104–128.Google Scholar
Biferale, L., Meneveau, C. & Verzicco, R. 2014 Deformation statistics of sub-Kolmogorov-scale ellipsoidal neutrally buoyant drops in isotropic turbulence. J. Fluid Mech. 754, 184–207.CrossRefGoogle Scholar
Byron, M., Einarsson, J., Gustavsson, K., Voth, G., Mehlig, B. & Variano, E. 2015 Shape-dependence of particle rotation in isotropic turbulence. Phys. Fluids 27 (3), 035101.CrossRefGoogle Scholar
Chaffey, C. E. & Brenner, H. 1967 A second-order theory for shear deformation of drops. J. Colloid Interface Sci. 24 (2), 258–269.Google Scholar
Chevillard, L. & Meneveau, C. 2013 Orientation dynamics of small, triaxial-ellipsoidal particles in isotropic turbulence. J. Fluid Mech. 737, 571–596.Google Scholar
Cox, R. G. 1969 The deformation of a drop in a general time-dependent fluid flow. J. Fluid Mech. 37 (03), 601–623.Google Scholar
Cristini, V., Blawzdziewicz, J., Loewenberg, M. & Collins, L. R. 2003 Breakup in stochastic Stokes flows: sub-Kolmogorov drops in isotropic turbulence. J. Fluid Mech. 492, 231–250.CrossRefGoogle Scholar
Dabiri, S., Lu, J. & Tryggvason, G. 2013 Transition between regimes of a vertical channel bubbly upflow due to bubble deformability. Phys. Fluids 25 (10), 102110.Google Scholar
Eaton, J. K & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2000 Scaling of global momentum transport in Taylor–Couette and pipe flow. Eur. Phys. J. B 18 (3), 541–544.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007a Fluxes and energy dissipation in thermal convection and shear flows. Europhys. Lett. 78 (2), 24001.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007b Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.CrossRefGoogle Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52 (4), 309–329.CrossRefGoogle Scholar
Frankel, N. A. & Acrivos, A. 1970 The constitutive equation for a dilute emulsion. J. Fluid Mech. 44 (01), 65–78.CrossRefGoogle Scholar
van Gils, D. P. M., Narezo Guzman, D., Sun, C. & Lohse, D. 2013 The importance of bubble deformability for strong drag reduction in bubbly turbulent Taylor–Couette flow. J. Fluid Mech. 722, 317–347.CrossRefGoogle Scholar
Girimaji, S. S. & Pope, S. B. 1990 Material-element deformation in isotropic turbulence. J. Fluid Mech. 220, 427–458.Google Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48, 53–80.Google Scholar
Guido, S., Minale, M. & Maffettone, P. L. 2000 Drop shape dynamics under shear-flow reversal. J. Rheol. 44 (6), 1385–1399.CrossRefGoogle Scholar
Guido, S. & Villone, M. 1998 Three-dimensional shape of a drop under simple shear flow. J. Rheol. 42 (2), 395–415.CrossRefGoogle Scholar
Hinze, J. O. 1955 Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1 (3), 289–295.Google Scholar
Johnson, P. L. & Meneveau, C. 2015 Large-deviation joint statistics of the finite-time Lyapunov spectrum in isotropic turbulence. Phys. Fluids 27 (8), 085110.Google Scholar
Kolmogorov, A. N. 1949 On the disintegration of drops in a turbulent flow. Dokl. Akad. Nauk SSSR 66, 30.Google Scholar
Lu, J., Fernández, A. & Tryggvason, G. 2005 The effect of bubbles on the wall drag in a turbulent channel flow. Phys. Fluids 17 (9), 095102.Google Scholar
Lu, J. & Tryggvason, G. 2008 Effect of bubble deformability in turbulent bubbly upflow in a vertical channel. Phys. Fluids 20 (4), 040701.Google Scholar
Lund, T. S. & Rogers, M. M. 1994 An improved measure of strain state probability in turbulent flows. Phys. Fluids 6 (5), 1838–1847.Google Scholar
Maffettone, P. L. & Minale, M. 1998 Equation of change for ellipsoidal drops in viscous flow. J. Non-Newtonian Fluid Mech. 78 (2), 227–241.CrossRefGoogle Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32 (1), 659–708.Google Scholar
Marchioli, C., Fantoni, M. & Soldati, A. 2010 Orientation, distribution, and deposition of elongated, inertial fibers in turbulent channel flow. Phys. Fluids 22 (3), 033301.CrossRefGoogle Scholar
Marchioli, C. & Soldati, A. 2015 Turbulent breakage of ductile aggregates. Phys. Rev. E 91 (5), 053003.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.CrossRefGoogle Scholar
Minale, M. 2008 A phenomenological model for wall effects on the deformation of an ellipsoidal drop in viscous flow. Rheol. Acta 47 (5–6), 667–675.Google Scholar
Minale, M. 2010 Models for the deformation of a single ellipsoidal drop: a review. Rheol. Acta 49 (8), 789–806.Google Scholar
Mortensen, P. H., Andersson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2008 On the orientation of ellipsoidal particles in a turbulent shear flow. Intl J. Multiphase Flow 34 (7), 678–683.CrossRefGoogle Scholar
Ni, R., Kramel, S., Ouellette, N. T. & Voth, G. A. 2015 Measurements of the coupling between the tumbling of rods and the velocity gradient tensor in turbulence. J. Fluids Mech. 766, 202–225.Google Scholar
Njobuenwu, D. O. & Fairweather, M. 2015 Dynamics of single, non-spherical ellipsoidal particles in a turbulent channel flow. Chem. Engng Sci. 123, 265–282.CrossRefGoogle Scholar
Ostilla-Mónico, R., Huisman, S. G., Jannink, T. J. G., Van Gils, D. P. M., Verzicco, R., Grossmann, S., Sun, C. & Lohse, D. 2014a Optimal Taylor–Couette flow: radius ratio dependence. J. Fluid Mech. 747, 1–29.CrossRefGoogle Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014b Boundary layer dynamics at the transition between the classical and the ultimate regime of Taylor–Couette flow. Phys. Fluids 26 (1), 015114.CrossRefGoogle Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014c Exploring the phase diagram of fully turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.Google Scholar
Ostilla-Mónico, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.Google Scholar
Ostilla-Mónico, R., Verzicco, R. & Lohse, D. 2015 Effects of the computational domain size on direct numerical simulations of Taylor–Couette turbulence with stationary outer cylinder. Phys. Fluids 27 (2), 025110.CrossRefGoogle Scholar
Parsa, S., Calzavarini, E., Toschi, F. & Voth, G. A. 2012 Rotation rate of rods in turbulent fluid flow. Phys. Rev. Lett. 109 (13), 134501.CrossRefGoogle ScholarPubMed
Perlekar, P., Biferale, L., Sbragaglia, M., Srivastava, S. & Toschi, F. 2012 Droplet size distribution in homogeneous isotropic turbulence. Phys. Fluids. 24 (6), 065101.Google Scholar
van der Poel, E. P., Ostilla-Mónico, R., Donners, J. & Verzicco, R. 2015 A pencil distributed finite difference code for strongly turbulent wall-bounded flows. Comput. Fluids 116, 10–16.CrossRefGoogle Scholar
Rallison, J. M. 1984 The deformation of small viscous drops and bubbles in shear flows. Annu. Rev. Fluid Mech. 16 (1), 45–66.Google Scholar
Shin, M. & Koch, D. L. 2005 Rotational and translational dispersion of fibres in isotropic turbulent flows. J. Fluid Mech. 540, 143–173.Google Scholar
Spandan, V., Ostilla-Mónico, R., Verzicco, R. & Lohse, D. 2016 Drag reduction in numerical two-phase Taylor–Couette turbulence using an Euler–Lagrange approach. J. Fluid Mech. 798, 411–435.Google Scholar
Stone, H. A. 1994 Dynamics of drop deformation and breakup in viscous fluids. Annu. Rev. Fluid Mech. 26 (1), 65–102.Google Scholar
Taylor, G. I. 1932 The viscosity of a fluid containing small drops of another fluid. Proc. R. Soc. Lond. 138, 41–48.Google Scholar
Taylor, G. I. 1934 The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. 146, 501–523.Google Scholar
Tryggvason, G., Dabiri, S., Aboulhasanzadeh, B. & Lu, J. 2013 Multiscale considerations in direct numerical simulations of multiphase flows. Phys. Fluids 25 (3), 031302.Google Scholar
de Tullio, M. D., Nam, J., Pascazio, G., Balaras, E. & Verzicco, R. 2012 Computational prediction of mechanical hemolysis in aortic valved prostheses. Eur. J. Mech. (B/Fluids) 35, 47–53.CrossRefGoogle Scholar
Vananroye, A., Van Puyvelde, P. & Moldenaers, P. 2011 Deformation and orientation of single droplets during shear flow: combined effects of confinement and compatibilization. Rheol. Acta 50 (3), 231–242.CrossRefGoogle Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123 (2), 402–414.Google Scholar