Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T09:32:25.594Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulations of instability and boundary layer turbulence under a solitary wave

Published online by Cambridge University Press:  28 August 2013

Celalettin E. Ozdemir ,
Tian-Jian Hsu  and
S. Balachandar
Celalettin E. Ozdemir*
Affiliation:
Center for Applied Coastal Research, University of Delaware, Newark, DE 19716, USA
Tian-Jian Hsu
Affiliation:
Center for Applied Coastal Research, University of Delaware, Newark, DE 19716, USA
S. Balachandar
Affiliation:
Mechanical & Aerospace Engineering, University of Florida, Gainesville, FL 32611, USA
*
†Current Address: Applied Ocean Physics & Engineering Department, Woods Hole Oceanographic Institution, 02543, Woods Hole, MA, USA. Email address for correspondence: cozdemir@whoi.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A significant amount of research effort has been made to understand the boundary layer instability and the generation and evolution of turbulence subject to periodic/oscillatory flows. However, little is known about bottom boundary layers driven by highly transient and intermittent free-stream flow forcing, such as solitary wave motion. To better understand the nature of the instability mechanisms and turbulent flow characteristics subject to solitary wave motion, a large number of direct numerical simulations are conducted. Different amplitudes of random initial fluctuating velocity field are imposed. Two different instability mechanisms are observed within the range of Reynolds number studied. The first is a short-lived, nonlinear, long-wave instability which is observed during the acceleration phase, and the second is a broadband instability that occurs during the deceleration phase. Transition from a laminar to turbulent state is observed to follow two different breakdown pathways: the first follows the sequence of 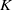$K$-type secondary instability of a near-wall boundary layer at comparatively lower Reynolds number and the second one follows a breakdown path similar to that of free shear layers. Overall characteristics of the flow are categorized into four regimes as: (i) laminar; (ii) disturbed laminar; (iii) transitional; and (iv) turbulent. Our categorization into four regimes is consistent with earlier works. However, this study is able to provide more specific definitions through the instability characteristics and the turbulence breakdown process.

JFM classification

Geophysical and Geological Flows: Coastal engineering Waves/Free-surface Flows: Solitary waves Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 731 , 25 September 2013 , pp. 545 - 578
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Apel, J. R., Byrne, H. M., Proni, J. R. & Charnell, R. L. 1975 Observations of oceanic internal and surface waves from the earth resources technology satellite. J. Geophys. Res. 80 (6), 865–881.Google Scholar
Blondeaux, P. & Vittori, G. 2012 RANS modelling of the turbulent boundary layer under a solitary wave. Coast. Engng 60, 1–10.CrossRefGoogle Scholar
Blondeaux, P., Pralits, J. & Vittori, G. 2012 Transition to turbulence at the bottom of a solitary wave. J. Fluid Mech. 709, 396–407.CrossRefGoogle Scholar
Bogucki, D. J., Rodekopp, L. G. & Barth, J. 2005 Internal solitary waves in the coastal mixing and optics 1996 experiment: multimodal structure and resuspension. J. Geophys. Res. 110, C02024.Google Scholar
Cantero, M. I., Balachandar, S. & Garcia, M. 2008 An Eulerian–Eulerian model for gravity currents driven by inertial particles. Intl J. Multiphase Flow 34, 484–501.CrossRefGoogle Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1987 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Cortese, T. & Balachandar, S. 1995 High performance spectral simulation of turbulent flows in massively parallel machines with distributed memory. Intl J. Supercomput. Appl. 9 (3), 187–204.Google Scholar
Dawson, A. G. & Shi, S. 2000 Tsunami deposits. Pure Appl. Geophys. 157, 875–897.CrossRefGoogle Scholar
Diamessis, P. J. & Rodekopp, L. G. 2006 Numerical investigation of solitary internal wave-induced global instability in shallow water benthic boundary layers. J. Phys. Oceanogr. 36, 784–812.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Grimshaw, R. 1971 The solitary wave in water of variable depth. J. Fluid Mech. 46, 611–622.Google Scholar
Kachanov, Y. S., Kozlov, V. V. & Levchenko, V. Y. 1977 Nonlinear development of a wave in a boundary layer. Fluid Dyn. 12, 383–390.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Lin, Y. & Rodekopp, L. G. 2011 The wave-induced boundary layer under long internal waves. Ocean Dyn. 61, 1045–1065.CrossRefGoogle Scholar
Liu, P. L.-F. & Orfilia, A. 2004 Viscous effects on transient long-wave propagation. J. Fluid Mech. 520, 83–92.CrossRefGoogle Scholar
Liu, P. L.-F., Park, Y. S. & Cowen, E. A. 2007 Boundary layer flow and bed shear stress under a solitary wave. J. Fluid Mech. 574, 449–463.CrossRefGoogle Scholar
Negretti, M. E. & Socolofsky, S. A. 2005 Stabilization of cylinder wakes in shallow water flows by means of roughness elements: an experimental study. Exp. Fluids 38, 403–414.Google Scholar
Seol, D. G. & Jirka, G. H. 2010 Quasi-tow dimensional properties of single shallow vortex with high initial Reynolds numbers. J. Fluid Mech. 665, 274–299.CrossRefGoogle Scholar
Son, S., Lynett, P. J. & Kim, D.-H. 2011 Nested and multi-physics modelling of tsunami evolution from generation to inundation. Ocean Model. 38 (1–2), 96–113.CrossRefGoogle Scholar
Spalart, & Baldwin, 1989 Direct simulation of a turbulent oscillating boundary layer. In Turbulent Shear Flows 6 (ed. Andre, J. C.), pp. 417–440. Springer.CrossRefGoogle Scholar
Stastna, M. & Lamb, K. G. 2002 Vortex shedding and sediment resuspension associated with the interaction of an internal solitary wave and the bottom boundary layer. Geophys. Res. Lett. 29 (11), 7-1–7-3.CrossRefGoogle Scholar
Sumer, B. M., Jensen, P. M., Søerensen, L. B., Fredsøe, J. & Liu, P. L. F. 2010 Coherent structures in wave boundary layers. Part 2. Solitary motion. J. Fluid Mech. 646, 207–231.Google Scholar
Synolakis, C. E., E. N., Bernard, Titov, V. V., Kânoğlu, U. & González, F. I. 2008 Validation and verification of tsunami numerical models. Pure Appl. Geophys. 165 (11–12), 2197–2228.CrossRefGoogle Scholar
Tonkin, S., Yeh, H., Kato, F. & Sato, S. 2003 Tsunami scour around a cylinder. J. Fluid Mech. 496, 165–192.CrossRefGoogle Scholar
Vittori, G. & Blondeaux, P. 2008 Turbulent boundary layer under a solitary wave. J. Fluid Mech. 615, 433–443.CrossRefGoogle Scholar
Vittori, G. & Blondeaux, P. 2011 Characteristics of the boundary layer at the bottom of a solitary wave. Coast. Engng 58, 206–213.CrossRefGoogle Scholar
Voit, S. S. 1987 Tsunamis. Annu. Rev. Fluid Mech. 19, 217–236.CrossRefGoogle Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar