Hostname: page-component-66d9dcfd78-8zft9 Total loading time: 0 Render date: 2026-08-08T04:16:09.961Z Has data issue: false hasContentIssue false
  • English
  • Français

Drops on soft solids: free energy and double transition of contact angles

Published online by Cambridge University Press:  10 April 2014

L. A. Lubbers ,
J. H. Weijs ,
L. Botto ,
S. Das ,
B. Andreotti  and
J. H. Snoeijer
L. A. Lubbers
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, Mesa+ Institute, University of Twente, 7500 AE Enschede, The Netherlands
J. H. Weijs*
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, Mesa+ Institute, University of Twente, 7500 AE Enschede, The Netherlands
L. Botto
Affiliation:
School of Engineering and Materials Science, Queen Mary University of London, London E1 4NS, UK
S. Das
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
B. Andreotti
Affiliation:
Physique et Mécanique des Milieux Hétérogènes, UMR 7636 ESPCI-CNRS, Univ. Paris-Diderot, 10 rue Vauquelin, 75005, Paris, France
J. H. Snoeijer
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, Mesa+ Institute, University of Twente, 7500 AE Enschede, The Netherlands Department of Applied Physics, Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, The Netherlands
*
†Email address for correspondence: j.h.weijs@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

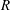The equilibrium shape of liquid drops on elastic substrates is determined by minimizing elastic and capillary free energies, focusing on thick incompressible substrates. The problem is governed by three length scales: the size of the drop $R$ , the molecular size $a$ and the ratio of surface tension to elastic modulus 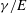$\gamma /E$ . We show that the contact angles undergo two transitions upon changing the substrate from rigid to soft. The microscopic wetting angles deviate from Young’s law when 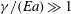$\gamma /(Ea)\gg 1$ , while the apparent macroscopic angle only changes in the very soft limit 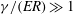$\gamma /(ER)\gg 1$ . The elastic deformations are worked out for the simplifying case where the solid surface energy is assumed to be constant. The total free energy turns out to be lower on softer substrates, consistent with recent experiments.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Contact lines Drops and Bubbles: Drops

Information

Type
Rapids
Information
Journal of Fluid Mechanics , Volume 747 , 25 May 2014 , R1
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Carre, A., Gastel, J. C. & Shanahan, M. E. R. 1996 Viscoelastic effects in the spreading of liquids. Nature 379 (6564), 432–434.CrossRefGoogle Scholar
Das, S., Marchand, A., Andreotti, B. & Snoeijer, J. H. 2011 Elastic deformation due to tangential capillary forces. Phys. Fluids 23 (7), 072006.Google Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quere, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
Jerison, E. R., Xu, Y., Wilen, L. A. & Dufresne, E. R. 2011 Deformation of an elastic substrate by a three-phase contact line. Phys. Rev. Lett. 106 (18), 186103.Google Scholar
Lester, G. R. 1961 Contact angles of liquids at deformable solid surfaces. J. Colloid Sci. 16 (4), 315–326.Google Scholar
Li, G., Graf, K., Bonaccurso, E., Golovko, D. S., Best, A. & Butt, H.-J. 2007 Evaporation structures of solvent drops evaporating from polymer surfaces: influence of molar mass. Macromol. Chem. Phys. 208 (19–20), 2134–2144.CrossRefGoogle Scholar
Limat, L. 2012 Straight contact lines on a soft, incompressible solid. Eur. Phys. J. E 35 (12), 134.Google Scholar
Long, D., Ajdari, A. & Leibler, L. 1996 Static and dynamic wetting properties of thin rubber films. Langmuir 12 (21), 5221–5230.CrossRefGoogle Scholar
Marchand, A., Das, S., Snoeijer, J. H. & Andreotti, B. 2012a Capillary pressure and contact line force on a soft solid. Phys. Rev. Lett. 108, 094301.Google Scholar
Marchand, A., Das, S., Snoeijer, J. H. & Andreotti, B. 2012b Contact angles on a soft solid: from Young’s law to Neumann’s law. Phys. Rev. Lett. 109 (23), 236101.Google Scholar
Marchand, A., Weijs, J. H., Snoeijer, J. H. & Andreotti, B. 2011 Why is surface tension a force parallel to the interface? Am. J. Phys. 79 (10), 999–1008.Google Scholar
Pericet-Camara, R., Best, A., Butt, H.-J. & Bonaccurso, E. 2008a Effect of capillary pressure and surface tension on the deformation of elastic surfaces by sessile liquid microdrops: an experimental investigation. Langmuir 24 (19), 10565–10568.CrossRefGoogle ScholarPubMed
Pericet-Camara, R., Bonaccurso, E. & Graf, K. 2008b Microstructuring of polystyrene surfaces with nonsolvent sessile droplets. ChemPhysChem 9 (12), 1738–1746.CrossRefGoogle ScholarPubMed
Rusanov, A. I. 1975 Theory of wetting of elastically deformed bodies. 1. Deformation with a finite contact-angle. Colloid J. USSR 37 (4), 614–622.Google Scholar
Rusanov, A. I. 1978 Thermodynamics of deformable solid-surfaces. J. Colloid Interface Sci. 63 (2), 330–345.Google Scholar
Shanahan, M. E. R. 1987 The influence of solid micro-deformation on contact-angle equilibrium. J. Phys. D: Appl. Phys. 20 (7), 945–950.Google Scholar
Shuttleworth, R. 1950 The surface tension of solids. Proc. Phys. Soc. Lond. A 63 (365), 444–457.Google Scholar
Sokuler, M., Auernhammer, G. K., Roth, M., Liu, C., Bonaccurso, E. & Butt, H.-J. 2010 The softer the better: fast condensation on soft surfaces. Langmuir 26 (3), 1544–1547.Google Scholar
Style, R. W., Boltyanskiy, R., Che, Y., Wettlaufer, J. S., Wilen, L. A. & Dufresne, E. R. 2013a Universal deformation of soft substrates near a contact line and the direct measurement of solid surface stresses. Phys. Rev. Lett. 110, 066103.CrossRefGoogle Scholar
Style, R. W., Che, Y., Park, S. J., Weon, B. M., Je, J. H., Hyland, C., German, G. K., Power, M. P., Wilen, L. A., Wettlaufer, J. S. & Dufresne, E. R. 2013b Patterning droplets with durotaxis. Proc. Natl Acad. Sci. USA.CrossRefGoogle ScholarPubMed
Style, R. W. & Dufresne, E. R. 2012 Static wetting on deformable substrates, from liquids to soft solids. Soft Matt. 8 (27), 7177–7184.Google Scholar
Weijs, J. H., Andreotti, B. & Snoeijer, J. H. 2013 Elasto-capillarity at the nanoscale: on the coupling between elasticity and surface energy in soft solids. Soft Matt. 9, 8494–8503.Google Scholar
White, L. R. 2003 The contact angle on an elastic substrate. 1. The role of disjoining pressure in the surface mechanics. J. Colloid Interface Sci. 258 (1), 82–96.Google Scholar