Article contents
A dynamical instability due to fluid–wall coupling lowers the transition Reynolds number in the flow through a flexible tube
Published online by Cambridge University Press: 02 August 2011
Abstract
A flow-induced instability in a tube with flexible walls is studied experimentally. Tubes of diameter 0.8 and 1.2 mm are cast in polydimethylsiloxane (PDMS) polymer gels, and the catalyst concentration in these gels is varied to obtain shear modulus in the range 17–550 kPa. A pressure drop between the inlet and outlet of the tube is used to drive fluid flow, and the friction factor 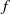 is measured as a function of the Reynolds number
is measured as a function of the Reynolds number 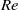 . From these measurements, it is found that the laminar flow becomes unstable, and there is a transition to a more complicated flow profile, for Reynolds numbers as low as 500 for the softest gels used here. The nature of the
. From these measurements, it is found that the laminar flow becomes unstable, and there is a transition to a more complicated flow profile, for Reynolds numbers as low as 500 for the softest gels used here. The nature of the 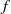 –
–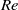 curves is also qualitatively different from that in the flow past rigid tubes; in contrast to the discontinuous increase in the friction factor at transition in a rigid tube, it is found that there is a continuous increase in the friction factor from the laminar value of
curves is also qualitatively different from that in the flow past rigid tubes; in contrast to the discontinuous increase in the friction factor at transition in a rigid tube, it is found that there is a continuous increase in the friction factor from the laminar value of 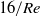 in a flexible tube. The onset of transition is also detected by a dye-stream method, where a stream of dye is injected into the centre of the tube. It is found that there is a continuous increase of the amplitude of perturbations at the onset of transition in a flexible tube, in contrast to the abrupt disruption of the dye stream at transition in a rigid tube. There are oscillations in the wall of the tube at the onset of transition, which is detected from the laser scattering off the walls of the tube. This indicates that the coupling between the fluid stresses and the elastic stresses in the wall results in an instability of the laminar flow.
in a flexible tube. The onset of transition is also detected by a dye-stream method, where a stream of dye is injected into the centre of the tube. It is found that there is a continuous increase of the amplitude of perturbations at the onset of transition in a flexible tube, in contrast to the abrupt disruption of the dye stream at transition in a rigid tube. There are oscillations in the wall of the tube at the onset of transition, which is detected from the laser scattering off the walls of the tube. This indicates that the coupling between the fluid stresses and the elastic stresses in the wall results in an instability of the laminar flow.
JFM classification
Information
- Type
- Papers
- Information
- Journal of Fluid Mechanics , Volume 705: Special issue dedicated to Professor T. J. Pedley on his 70th birthday , 25 August 2012 , pp. 322 - 347
- Copyright
- Copyright © Cambridge University Press 2011
References
- 49
- Cited by

