Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhu, Lu
and
Xi, Li
2019.
Vortex dynamics in low- and high-extent polymer drag reduction regimes revealed by vortex tracking and conformation analysis.
Physics of Fluids,
Vol. 31,
Issue. 9,
Xi, Li
2019.
Turbulent drag reduction by polymer additives: Fundamentals and recent advances.
Physics of Fluids,
Vol. 31,
Issue. 12,
Song, Jiaxing
Teng, Hao
Liu, Nansheng
Ding, Hang
Lu, Xi-Yun
and
Khomami, Bamin
2019.
The correspondence between drag enhancement and vortical structures in turbulent Taylor–Couette flows with polymer additives: a study of curvature dependence.
Journal of Fluid Mechanics,
Vol. 881,
Issue. ,
p.
602.
Zhu, Yabiao
Song, Jiaxing
Liu, Nansheng
Lu, Xiyun
and
Khomami, Bamin
2020.
Polymer-induced flow relaminarization and drag enhancement in spanwise-rotating plane Couette flow.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
López, Jose Manuel
Feldmann, Daniel
Rampp, Markus
Vela-Martín, Alberto
Shi, Liang
and
Avila, Marc
2020.
nsCouette – A high-performance code for direct numerical simulations of turbulent Taylor–Couette flow.
SoftwareX,
Vol. 11,
Issue. ,
p.
100395.
Zhu, Lu
and
Xi, Li
2020.
Inertia-driven and elastoinertial viscoelastic turbulent channel flow simulated with a hybrid pseudo-spectral/finite-difference numerical scheme.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 286,
Issue. ,
p.
104410.
Malik, M.
Bouffanais, Roland
and
Skote, Martin
2020.
Viscoelastic laminar drag bounds in pipe flow.
Physics of Fluids,
Vol. 32,
Issue. 3,
Peng, Sai
Xiong, Yong-Liang
Xu, Xiao-Yang
and
Yu, Peng
2020.
Numerical study of unsteady viscoelastic flow past two side-by-side circular cylinders.
Physics of Fluids,
Vol. 32,
Issue. 8,
Shekar, Ashwin
McMullen, Ryan M.
McKeon, Beverley J.
and
Graham, Michael D.
2020.
Self-sustained elastoinertial Tollmien–Schlichting waves.
Journal of Fluid Mechanics,
Vol. 897,
Issue. ,
Dubief, Yves
and
Terrapon, Vincent E.
2020.
Heat transfer enhancement and reduction in low-Rayleigh number natural convection flow with polymer additives.
Physics of Fluids,
Vol. 32,
Issue. 3,
Sun, Guangrui
Wan, Dongdong
and
Zhang, Mengqi
2021.
Nonlinear evolutions of streaky structures in viscoelastic pipe flows.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 295,
Issue. ,
p.
104622.
Yamani, Sami
Keshavarz, Bavand
Raj, Yashasvi
Zaki, Tamer A.
McKinley, Gareth H.
and
Bischofberger, Irmgard
2021.
Spectral Universality of Elastoinertial Turbulence.
Physical Review Letters,
Vol. 127,
Issue. 7,
Shekar, Ashwin
McMullen, Ryan M.
McKeon, Beverley J.
and
Graham, Michael D.
2021.
Tollmien-Schlichting route to elastoinertial turbulence in channel flow.
Physical Review Fluids,
Vol. 6,
Issue. 9,
Peng, Sai
Li, Jia-yu
Xiong, Yong-liang
Xu, Xiao-yang
and
Yu, Peng
2021.
Numerical simulation of two-dimensional unsteady Giesekus flow over a circular cylinder.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 294,
Issue. ,
p.
104571.
Kobayashi, Yusei
Gomyo, Hirotaka
and
Arai, Noriyoshi
2021.
Molecular Insight into the Possible Mechanism of Drag Reduction of Surfactant Aqueous Solution in Pipe Flow.
International Journal of Molecular Sciences,
Vol. 22,
Issue. 14,
p.
7573.
Chaudhary, Indresh
Garg, Piyush
Subramanian, Ganesh
and
Shankar, V.
2021.
Linear instability of viscoelastic pipe flow.
Journal of Fluid Mechanics,
Vol. 908,
Issue. ,
Zhang, Wen-Hua
Zhang, Hong-Na
Li, Yu-Ke
Yu, Bo
and
Li, Feng-Chen
2021.
Role of elasto-inertial turbulence in viscoelastic drag-reducing turbulence.
Physics of Fluids,
Vol. 33,
Issue. 8,
Khalid, Mohammad
Shankar, V.
and
Subramanian, Ganesh
2021.
Continuous Pathway between the Elasto-Inertial and Elastic Turbulent States in Viscoelastic Channel Flow.
Physical Review Letters,
Vol. 127,
Issue. 13,
Zhu, Lu
and
Xi, Li
2021.
Nonasymptotic elastoinertial turbulence for asymptotic drag reduction.
Physical Review Fluids,
Vol. 6,
Issue. 1,
Cai, Hui
and
Miao, Guoqing
2021.
Laminar and turbulent flows in a vibrated granular system.
Powder Technology,
Vol. 380,
Issue. ,
p.
89.
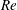 $Re$) using minimal sized channels appeared to support this view and reported long ‘hibernation’ periods where turbulence is marginalized. In simulations of pipe flow at
$Re$) using minimal sized channels appeared to support this view and reported long ‘hibernation’ periods where turbulence is marginalized. In simulations of pipe flow at 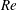 $Re$ near transition we find that, indeed, with increasing Weissenberg number (
$Re$ near transition we find that, indeed, with increasing Weissenberg number (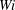 $Wi$), turbulence expresses long periods of hibernation if the domain size is small. However, with increasing pipe length, the temporal hibernation continuously alters to spatio-temporal intermittency and here the flow consists of turbulent puffs surrounded by laminar flow. Moreover, upon an increase in
$Wi$), turbulence expresses long periods of hibernation if the domain size is small. However, with increasing pipe length, the temporal hibernation continuously alters to spatio-temporal intermittency and here the flow consists of turbulent puffs surrounded by laminar flow. Moreover, upon an increase in 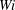 $Wi$, the flow fully relaminarizes, in agreement with recent experiments. At even larger
$Wi$, the flow fully relaminarizes, in agreement with recent experiments. At even larger 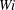 $Wi$, a different instability is encountered causing a drag increase towards MDR. Our findings hence link earlier minimal flow unit simulations with recent experiments and confirm that the addition of polymers initially suppresses Newtonian turbulence and leads to a reverse transition. The MDR state on the other hand results at these low
$Wi$, a different instability is encountered causing a drag increase towards MDR. Our findings hence link earlier minimal flow unit simulations with recent experiments and confirm that the addition of polymers initially suppresses Newtonian turbulence and leads to a reverse transition. The MDR state on the other hand results at these low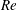 $Re$ from a separate instability and the underlying dynamics corresponds to the recently proposed state of elasto-inertial turbulence.
$Re$ from a separate instability and the underlying dynamics corresponds to the recently proposed state of elasto-inertial turbulence.

