Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Richter, David
Shaqfeh, Eric S. G.
and
Iaccarino, Gianluca
2011.
Numerical Simulation of Polymer Injection in Turbulent Flow Past a Circular Cylinder.
Journal of Fluids Engineering,
Vol. 133,
Issue. 10,
Xiong, Y.L.
Bruneau, C.H.
and
Kellay, H.
2013.
A numerical study of two dimensional flows past a bluff body for dilute polymer solutions.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 196,
Issue. ,
p.
8.
Naseri, Homa
Koukouvinis, Phoevos
Malgarinos, Ilias
and
Gavaises, Manolis
2018.
On viscoelastic cavitating flows: A numerical study.
Physics of Fluids,
Vol. 30,
Issue. 3,
Hou, RuYi
Peng, Sai
Xiong, Yongliang
and
Yang, Dan
2018.
Influence of polymer additive on flow past an underwater slender body.
p.
1.
Xiong, Yongliang
Peng, Sai
Zhang, Mengqi
and
Yang, Dan
2019.
Numerical study on the vortex-induced vibration of a circular cylinder in viscoelastic fluids.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 272,
Issue. ,
p.
104170.
Peng, Sai
Xiong, Yong-Liang
Xu, Xiao-Yang
and
Yu, Peng
2020.
Numerical study of unsteady viscoelastic flow past two side-by-side circular cylinders.
Physics of Fluids,
Vol. 32,
Issue. 8,
Tian, Deqiang
Fan, Honghai
Leira, Bernt J
Sævik, Svein
and
Fu, Ping
2020.
Static analysis of interaction between two adjacent top tensioned risers with consideration of wake effects.
Ocean Engineering,
Vol. 195,
Issue. ,
p.
106662.
Peng, Sai
Li, Jia-yu
Xiong, Yong-liang
Xu, Xiao-yang
and
Yu, Peng
2021.
Numerical simulation of two-dimensional unsteady Giesekus flow over a circular cylinder.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 294,
Issue. ,
p.
104571.
Lee, Junghaeng
Hwang, Wook Ryol
and
Cho, Kwang Soo
2021.
Effect of stress diffusion on the Oldroyd-B fluid flow past a confined cylinder.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 297,
Issue. ,
p.
104650.
Chauhan, A.
Gupta, S.
and
Sasmal, C.
2022.
Effect of geometric disorder on chaotic viscoelastic porous media flows.
Physics of Fluids,
Vol. 34,
Issue. 9,
Singh, Abhinav
and
Narasimhamurthy, Vagesh D.
2022.
Perforation effects on the wake dynamics of normal flat plates.
Journal of Fluid Mechanics,
Vol. 947,
Issue. ,
Peng, Sai
Huang, Tao
Kouser, Taiba
Zhuang, Xiao-Ru
Xiong, Yong-Liang
and
Yu, Peng
2022.
Wake asymmetry weakening in viscoelastic fluids: Numerical discovery and mechanism exploration.
Physics of Fluids,
Vol. 34,
Issue. 9,
Minaeian, Ali
Nili-AhmadAbadi, Mahdi
Norouzi, Mahmood
and
Kim, Kyung Chun
2022.
Effects of viscoelasticity on the onset of vortex shedding and forces applied on a cylinder in unsteady flow regime.
Physics of Fluids,
Vol. 34,
Issue. 1,
Zargar, Arash
Tarokh, Ali
and
Hemmati, Arman
2022.
The unsteady wake transition behind a wall-mounted large-depth-ratio prism.
Journal of Fluid Mechanics,
Vol. 952,
Issue. ,
Bansal, D.
Chauhan, T.
and
Sircar, S.
2022.
Spatiotemporal linear stability of viscoelastic Saffman–Taylor flows.
Physics of Fluids,
Vol. 34,
Issue. 10,
Guimarães, Mateus C.
Pinho, Fernando T.
and
da Silva, Carlos B.
2022.
Turbulent planar wakes of viscoelastic fluids analysed by direct numerical simulations.
Journal of Fluid Mechanics,
Vol. 946,
Issue. ,
Song, Kaiyao
Jin, Guoyong
Jia, Di
Hua, Runan
Ye, Tiangui
Sun, Zexi
and
Liu, Zhigang
2023.
Effects of viscoelastic fluid on noise reduction of the flow over a circular cylinder.
Journal of Fluids and Structures,
Vol. 122,
Issue. ,
p.
103976.
Boersma, Pieter R.
Rothstein, Jonathan P.
and
Modarres-Sadeghi, Yahya
2023.
Experimental investigation of vortex-induced vibrations of a flexibly mounted cylinder in a shear-thinning fluid.
Physical Review Fluids,
Vol. 8,
Issue. 4,
Zhang, Jun-Qiang
Hou, Guo-Xiang
Xiong, Yong-Liang
and
Yang, Dan
2023.
Modified stable methods and effect of artificial diffusion in the numerical study of viscoelastic fluid flow.
Physics of Fluids,
Vol. 35,
Issue. 12,
Fukushima, Kengo
Kishi, Haruki
Sago, Ryotaro
Suzuki, Hiroshi
Poole, Robert J.
and
Hidema, Ruri
2024.
Polymer-doped two-dimensional turbulent flow to study the transition from Newtonian turbulence to elastic instability.
Physics of Fluids,
Vol. 36,
Issue. 10,
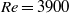 , Newtonian flow past a circular cylinder exhibits a wake and detached shear layers which have transitioned to turbulence. It is the goal of the present study to investigate the effects which viscoelasticity has on this state and to identify the mechanisms responsible for wake stabilization. It is found through numerical simulations (employing the FENE-P rheological model) that viscoelasticity greatly reduces the amount of turbulence in the wake, reverting it back to a state which qualitatively appears similar to the Newtonian mode B instability which occurs at lower
, Newtonian flow past a circular cylinder exhibits a wake and detached shear layers which have transitioned to turbulence. It is the goal of the present study to investigate the effects which viscoelasticity has on this state and to identify the mechanisms responsible for wake stabilization. It is found through numerical simulations (employing the FENE-P rheological model) that viscoelasticity greatly reduces the amount of turbulence in the wake, reverting it back to a state which qualitatively appears similar to the Newtonian mode B instability which occurs at lower 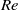 . By focusing on the separated shear layers, it is found that viscoelasticity suppresses the formation of the Kelvin–Helmholtz instability which dominates for Newtonian flows, consistent with previous studies of viscoelastic free shear layers. Through this shear layer stabilization, the viscoelastic far wake is then subject to the same instability mechanisms which dominate for Newtonian flows, but at far lower Reynolds numbers.
. By focusing on the separated shear layers, it is found that viscoelasticity suppresses the formation of the Kelvin–Helmholtz instability which dominates for Newtonian flows, consistent with previous studies of viscoelastic free shear layers. Through this shear layer stabilization, the viscoelastic far wake is then subject to the same instability mechanisms which dominate for Newtonian flows, but at far lower Reynolds numbers.
