Article contents
Electrophoresis of bubbles
Published online by Cambridge University Press: 16 July 2014
Abstract
Smoluchowski’s celebrated electrophoresis formula is inapplicable to field-driven motion of drops and bubbles with mobile interfaces. We here analyse bubble electrophoresis in the thin-double-layer limit. To this end, we employ a systematic asymptotic procedure starting from the standard electrokinetic equations and a simple physicochemical interface model. This furnishes a coarse-grained macroscale description where the Debye-layer physics is embodied in effective boundary conditions. These conditions, in turn, represent a non-conventional driving mechanism for electrokinetic flows, where bulk concentration polarization, engendered by the interaction of the electric field and the Debye layer, results in a Marangoni-like shear stress. Remarkably, the electro-osmotic velocity jump at the macroscale level does not affect the electrophoretic velocity. Regular approximations are obtained in the respective cases of small zeta potentials, small ions, and weak applied fields. The nonlinear small-zeta-potential approximation rationalizes the paradoxical zero mobility predicted by the linearized scheme of Booth (J. Chem. Phys., vol. 19, 1951, pp. 1331–1336). For large (millimetre-size) bubbles the pertinent limit is actually that of strong fields. We have carried out a matched-asymptotic-expansion analysis of this singular limit, where salt polarization is confined to a narrow diffusive layer. This analysis establishes that the bubble velocity scales as the 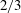 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}2/3$ -power of the applied-field magnitude and yields its explicit functional dependence upon a specific combination of the zeta potential and the ionic drag coefficient. The latter is provided to within an
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}2/3$ -power of the applied-field magnitude and yields its explicit functional dependence upon a specific combination of the zeta potential and the ionic drag coefficient. The latter is provided to within an 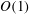 $O(1)$ numerical pre-factor which, in turn, is calculated via the solution of a universal (parameter-free) nonlinear flow problem. It is demonstrated that, with increasing field magnitude, all numerical solutions of the macroscale model indeed collapse on the analytic approximation thus obtained. Existing measurements of clean-bubble electrophoresis agree neither with present theory nor with previous models; we discuss this ongoing discrepancy.
$O(1)$ numerical pre-factor which, in turn, is calculated via the solution of a universal (parameter-free) nonlinear flow problem. It is demonstrated that, with increasing field magnitude, all numerical solutions of the macroscale model indeed collapse on the analytic approximation thus obtained. Existing measurements of clean-bubble electrophoresis agree neither with present theory nor with previous models; we discuss this ongoing discrepancy.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 42
- Cited by

