Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-30T05:52:54.239Z Has data issue: false hasContentIssue false
  • English
  • Français

Electrostatic forcing of thin leaky dielectric films under periodic and steady fields

Published online by Cambridge University Press:  13 March 2020

Dipin S. Pillai Open the ORCID record for Dipin S. Pillai [Opens in a new window]  and
R. Narayanan
Dipin S. Pillai*
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Kanpur, Kalyanpur, Uttar Pradesh 208016, India
R. Narayanan
Affiliation:
Department of Chemical Engineering, University of Florida, Gainesville, FL 32611, USA
*
†Email address for correspondence: dipinsp@iitk.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

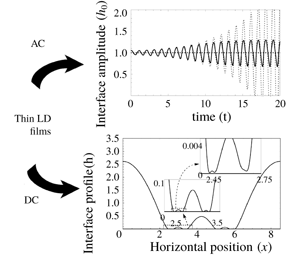
The linear and nonlinear dynamics of an interface separating a thin liquid film and a hydrodynamically passive ambient medium, subject to normal electrostatic forcing, are investigated. A reduced-order model is developed for the case where both fluids are taken to be leaky dielectrics (LD). Cases of time periodic as well as steady forcing are studied. In the former case, an important result is the elucidation of two forms of resonant instability than can occur in LD films. These correspond to an inertial resonance due to mechanical inertia of the fluid and an inertialess resonance due to charge capacitance at the interface that is similar to mechanically forced films with an insoluble surfactant. In the case of steady forcing, the long-time dynamics exhibits spontaneous sliding as the interface approaches the wall, for the two limiting cases of a perfect conductor–perfect dielectric pair as well as a pair of perfect dielectrics. Under these limits, only the normal component of the Maxwell stress at the interface is significant and the interface dynamics resembles that of a Rayleigh–Taylor unstable interface. For a general pair of leaky dielectrics studied in the limit of fast relaxation times, the presence of interfacial charge prevents the onset of sliding. For the special case when the square of the conductivity ratio equals the permittivity ratio, the interface exhibits cascading structures, similar to those reported for the long-wave Marangoni instability.

JFM classification

Drops and Bubbles: Electrohydrodynamic effects Interfacial Flows (free surface): Thin films Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 890 , 10 May 2020 , A20
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bandopadhyay, A. & Hardt, S. 2017 Stability of horizontal viscous fluid layers in a vertical arbitrary time periodic electric field. Phys. Fluids 29, 124101.CrossRefGoogle Scholar
Benjamin, T. B. & Ursell, F. 1954 The stability of the plane free surface of a liquid in vertical periodic motion. Proc. R. Soc. Lond. 121, 299–340.Google Scholar
Bestehorn, M. 2013 Laterally extended thin liquid films with inertia under external vibrations. Phys. Fluids 25, 114106.CrossRefGoogle Scholar
Boos, W. & Thess, A. 1999 Cascade of structures in long-wavelength Marangoni instability. Phys. Fluids 11, 1484–1494.CrossRefGoogle Scholar
Briskman, V. A. & Shaidurov, G. F. 1968 Parametric instability of a fluid surface in an alternating electric field. Sov. Phys. Dokl. 13, 540–542.Google Scholar
Burcham, C. L. & Saville, D. A. 2000 The electrohydrodynamic stability of a liquid bridge: microgravity experiments on a bridge suspended in a dielectric gas. J. Fluid Mech. 405, 37–56.CrossRefGoogle Scholar
Craster, R. V. & Matar, O. 2005 Electrically induced pattern formation in thin leaky dielectric films. Phys. Fluids 17, 032104.CrossRefGoogle Scholar
Dietze, G. F., Picardo, J. R. & Narayanan, R. 2018 Sliding instability of draining liquid films. J. Fluid Mech. 857, 111–141.CrossRefGoogle Scholar
Dietze, G. F. & Ruyer-Quil, C. 2013 Wavy liquid films in interaction with a confined laminar gas flow. J. Fluid Mech. 722, 348–393.CrossRefGoogle Scholar
Faraday, M. 1831 On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Phil. Trans. R. Soc. Lond. 121, 299–340.Google Scholar
Gambhire, P. & Thaokar, R. M. 2010 Electrohydrodynamic instabilities at interfaces subjected to alternating electric field. Phys. Fluids 22, 064103.CrossRefGoogle Scholar
Johns, L. E. 2016 The diffusion equation for a solute confined to a moving surface. Phys. Fluids 28, 032107.CrossRefGoogle Scholar
Kumar, K. 1996 Linear theory of Faraday instability in viscous liquids. Proc. R. Soc. Lond. A 452, 1113–1126.Google Scholar
Kumar, K. & Tuckerman, L. S. 1994 Parametric instability of the interface between two fluids. J. Fluid Mech. 279, 49–68.CrossRefGoogle Scholar
Kumar, S. & Matar, O. K. 2002 Instability of long-wavelength disturbances on gravity-modulated surfactant-covered thin liquid layers. J. Fluid Mech. 466, 249–258.CrossRefGoogle Scholar
Labrosse, G. 2011 Méthodes numériques : Méthodes spectrale : Méthodes locales globales, méthodes globales, problèmes d’Helmotz et de Stokes, équations de Navier–Stokes. Ellipses Marketing.Google Scholar
Lister, J. R., Morrison, N. F. & Rallison, J. M. 2006a Sedimentation of a two-dimensional drop towards a rigid horizontal plate. J. Fluid Mech. 552, 345–351.CrossRefGoogle Scholar
Lister, J. R., Rallison, J. M., King, A. A., Cummings, L. J. & Jensen, O. E. 2006b Capillary drainage of an annular film: the dynamics of collars and lobes. J. Fluid Mech. 552, 311–343.CrossRefGoogle Scholar
Lister, J. R., Rallison, J. M. & Rees, S. J. 2010 The nonlinear dynamics of pendent drops on a thin film coating the underside of a ceiling. J. Fluid Mech. 647, 239–264.CrossRefGoogle Scholar
Matar, O. K., Kumar, S. & Craster, R. V. 2004 Nonlinear parametric excited surface waves in surfactant-covered thin liquid films. J. Fluid Mech. 520, 243–265.CrossRefGoogle Scholar
Melcher, J. R. & Taylor, G. I. 1969 Electrohydrodynamics: a review of the role of interfacial shear stresses. Annu. Rev. Fluid Mech. 1, 111–146.CrossRefGoogle Scholar
Müller, H. W., Wittmer, H., Wagner, C., Albers, J. & Knorr, K. 1997 Analytic stability theory for Faraday waves and the observation of the harmonic surface response. Phys. Rev. Lett. 78, 2357–2360.CrossRefGoogle Scholar
Nayfeh, A. H. 1981 Introduction to Perturbation Techniques. Wiley.Google Scholar
Ozen, O., Aubry, N., Papageorgiou, D. T. & Petropoulos, P. G. 2006 Electrohydrodynamic linear stability of two immiscible fluids in channel flow. Electrochim. Acta 51, 5316–5323.CrossRefGoogle Scholar
Papageorgiou, D. T. 2019 Film flows in the presence of electric fields. Annu. Rev. Fluid Mech. 51, 155–187.CrossRefGoogle Scholar
Papageorgiou, D. T. & Petropoulos, P. G. 2004 Generation of interfacial instabilities in charged electrified viscous liquid films. J. Engng Maths 50, 223–240.CrossRefGoogle Scholar
Pillai, D. S. & Narayanan, R. 2018 Nonlinear dynamics of electrostatic Faraday instability in thin films. J. Fluid Mech. 855, R4.CrossRefGoogle Scholar
Rayleigh, L. 1833 On the crispations of fluid resting upon a vibrating support. Phil. Mag. 16, 50–58.CrossRefGoogle Scholar
Roberts, S. & Kumar, S. 2009 AC electrohydrodynamic instabilities in thin liquid films. J. Fluid Mech. 631, 255–279.CrossRefGoogle Scholar
Ruyer-Quil, C. & Manneville, P. 2002 Further accuracy and convergence results on the modeling of flows down inclined planes by weighted-residual approximations. Phys. Fluids 14, 170–183.CrossRefGoogle Scholar
Saville, D. A. 1997 Electrohydrodynamics: the Taylor–Melcher leaky dielectric model. Annu. Rev. Fluid Mech. 29, 27–64.CrossRefGoogle Scholar
Shankar, V. & Sharma, A. 2004 Instability of the interface between thin fluid films subjected to electric fields. J. Colloid Interface Sci. 274, 294–308.CrossRefGoogle ScholarPubMed
Suman, B. & Kumar, S. 2008 Surfactant- and elasticity-induced inertialess instabilities in vertically vibrated liquids. J. Fluid Mech. 610, 407–423.CrossRefGoogle Scholar
Tsai, S. C. & Tsai, C. S. 2013 Linear theory on temporal instability of Megahertz Faraday waves for monodisperse microdroplet ejection. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 60, 1746–1755.CrossRefGoogle ScholarPubMed
Uguz, A. K., Ozen, O. & Aubry, N. 2008 Electric field effect on a two-fluid interface instability in channel flow for fast electric times. Phys. Fluids 20, 031702.Google Scholar
Ward, K., Matsumoto, S. & Narayanan, R. 2019 The electrostatically forced Faraday instability – theory and experiments. J. Fluid Mech. 862, 696–731.CrossRefGoogle Scholar
Wray, A. W., Matar, O. K. & Papageorgiou, D. T. 2017 Accurate low-order modeling of electrified falling films at moderate Reynolds number. Phys. Rev. Fluids 2, 063701.CrossRefGoogle Scholar
Wu, L. & Chou, S. Y. 2003 Dynamic modeling and scaling of nanostructure formation in the lithographically induced self-assembly and self-construction. Appl. Phys. Lett. 82 (19), 3200–3202.CrossRefGoogle Scholar
Yiantsios, S. G. & Higgins, B. G. 1989 Rayleigh–Taylor instability in thin viscous films. Phys. Fluids 1, 1484–1501.CrossRefGoogle Scholar
Yih, C. S. 1968 Stability of horizontal fluid interface in a periodic vertical electric field. Phys. Fluids 11, 1447–1449.CrossRefGoogle Scholar

Pillai and Narayanan supplementary movie 1

Spatio-temporal evolution of subharmonic (SH) and harmonic (H) Faraday instability, exhibited by a pair of perfect dielectrics. Properties of silicone oil and air in table 1 are used for simulations. SH response corresponds to k=0.23, A=10.7kV and H response corresponds to k=0.42, A=13.1kV.

Download Pillai and Narayanan supplementary movie 1(Video)
Video 3.9 MB

Pillai and Narayanan supplementary movie 2

Evolution of interface between thin leaky dielectric films with σ=ε, exhibiting spontaneous sliding. This case corresponds to the condition of zero tangential stress. Similarly, sliding is also observed in the case of a pair of perfect dielectrics as well as a perfect conductor-perfect dielectric pair, where too the interface is solely under the influence of normal stress.

Download Pillai and Narayanan supplementary movie 2(Video)
Video 4.7 MB

Pillai and Narayanan supplementary movie 3

Long-time cascading structures exhibited by the interface between a pair of leaky dielectrics for the case of zero normal stress (i.e. σ=ε1/2). The interface evolution is due to the tangential component of Maxwell stress and undergoes a series of buckling events as it approaches the wall.

Download Pillai and Narayanan supplementary movie 3(Video)
Video 14.3 MB
Supplementary material: File

Pillai and Narayanan supplementary material

Supplementary data

Download Pillai and Narayanan supplementary material(File)
File 32.7 KB