Article contents
Experimental analysis of the effect of local base blowing on three-dimensional wake modes
Published online by Cambridge University Press: 28 November 2019
Abstract
Wake modes of a three-dimensional blunt-based body near a wall are investigated at a Reynolds number  $Re=10^{5}$. The targeted modes are the static symmetry-breaking mode and two antisymmetric periodic modes. The static mode orientation is aligned with the horizontal major
$Re=10^{5}$. The targeted modes are the static symmetry-breaking mode and two antisymmetric periodic modes. The static mode orientation is aligned with the horizontal major  $y$-axis of the base and randomly switches between a positive
$y$-axis of the base and randomly switches between a positive  $P$ and a negative
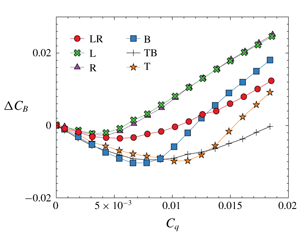
$P$ and a negative  $N$ state leading to long-time bistable dynamics of the turbulent wake. The modifications of these modes are studied when continuous blowing is applied at different locations through four slits along the base edges (denoted L for left, R for right, T for top and B for bottom) in either four single asymmetric configurations or two double symmetric configurations (denoted LR and TB). Two regimes, referred to as mass and momentum, are clearly identifiable for all configurations. The mass regime, which is fairly insensitive to blowing momentum and location, is characterized by the growth of the recirculating bubble as the total injected flow rate is increased, and is associated with a base drag reduction and interpreted as resulting from the equilibrium between mass fluxes feeding and emptying the recirculating region. A simple budget model is shown to be in agreement with entrainment velocities measured for isolated turbulent mixing layers. The strength of the static mode is reduced up to 20 % when the bubble length is maximum, whereas no change in the periodic mode frequencies is found. On the other hand, the momentum regime is characterized by the deflating of the recirculating bubble, leading to base drag increase, and it is interpreted by the free shear layer forcing, which increases the entrainment velocity, thus emptying the recirculating bubble. In this regime the static mode orientation is imposed by the blowing symmetry. Lateral L and R (respectively top/bottom T and B) blowing configurations select
$N$ state leading to long-time bistable dynamics of the turbulent wake. The modifications of these modes are studied when continuous blowing is applied at different locations through four slits along the base edges (denoted L for left, R for right, T for top and B for bottom) in either four single asymmetric configurations or two double symmetric configurations (denoted LR and TB). Two regimes, referred to as mass and momentum, are clearly identifiable for all configurations. The mass regime, which is fairly insensitive to blowing momentum and location, is characterized by the growth of the recirculating bubble as the total injected flow rate is increased, and is associated with a base drag reduction and interpreted as resulting from the equilibrium between mass fluxes feeding and emptying the recirculating region. A simple budget model is shown to be in agreement with entrainment velocities measured for isolated turbulent mixing layers. The strength of the static mode is reduced up to 20 % when the bubble length is maximum, whereas no change in the periodic mode frequencies is found. On the other hand, the momentum regime is characterized by the deflating of the recirculating bubble, leading to base drag increase, and it is interpreted by the free shear layer forcing, which increases the entrainment velocity, thus emptying the recirculating bubble. In this regime the static mode orientation is imposed by the blowing symmetry. Lateral L and R (respectively top/bottom T and B) blowing configurations select  $P$ or
$P$ or  $N$ states in the horizontal (respectively vertical) direction, while bistable dynamics persists for the symmetric LR and TB configurations. The shape of periodic modes follows the changes in wake static orientation. The transition between the two regimes is governed by both the total injected flow rate and the location of the injection.
$N$ states in the horizontal (respectively vertical) direction, while bistable dynamics persists for the symmetric LR and TB configurations. The shape of periodic modes follows the changes in wake static orientation. The transition between the two regimes is governed by both the total injected flow rate and the location of the injection.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 46
- Cited by

