Article contents
Experimental investigation of flow-induced vibration of a rotating circular cylinder
Published online by Cambridge University Press: 21 September 2017
Abstract
While flow-induced vibration of bluff bodies has been extensively studied over the last half-century, only limited attention has been given to flow-induced vibration of elastically mounted rotating cylinders. Since recent low-Reynolds-number numerical work suggests that rotation can enhance or suppress the natural oscillatory response, the former could find applications in energy harvesting and the latter in vibration control. The present experimental investigation characterises the dynamic response and wake structure of a rotating circular cylinder undergoing vortex-induced vibration at a low mass ratio (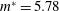 $m^{\ast }=5.78$ ) over the reduced velocity range leading to strong oscillations. The experiments were conducted in a free-surface water channel with the cylinder vertically mounted and attached to a motor that provided constant rotation. Springs and an air-bearing system allow the cylinder to undertake low-damped transverse oscillations. Under cylinder rotation, the normalised frequency response was found to be comparable to that of a freely vibrating non-rotating cylinder. At reduced velocities consistent with the upper branch of a non-rotating transversely oscillating cylinder, the maximum oscillation amplitude increased with non-dimensional rotation rate up to
$m^{\ast }=5.78$ ) over the reduced velocity range leading to strong oscillations. The experiments were conducted in a free-surface water channel with the cylinder vertically mounted and attached to a motor that provided constant rotation. Springs and an air-bearing system allow the cylinder to undertake low-damped transverse oscillations. Under cylinder rotation, the normalised frequency response was found to be comparable to that of a freely vibrating non-rotating cylinder. At reduced velocities consistent with the upper branch of a non-rotating transversely oscillating cylinder, the maximum oscillation amplitude increased with non-dimensional rotation rate up to 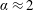 $\unicode[STIX]{x1D6FC}\approx 2$ . Beyond this, there was a sharp decrease in amplitude. Notably, this critical value corresponds approximately to the rotation rate at which vortex shedding ceases for a non-oscillating rotating cylinder. Remarkably, at
$\unicode[STIX]{x1D6FC}\approx 2$ . Beyond this, there was a sharp decrease in amplitude. Notably, this critical value corresponds approximately to the rotation rate at which vortex shedding ceases for a non-oscillating rotating cylinder. Remarkably, at 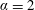 $\unicode[STIX]{x1D6FC}=2$ there was approximately an 80 % increase in the peak amplitude response compared to that of a non-rotating cylinder. The observed amplitude response measured over the Reynolds-number range of (
$\unicode[STIX]{x1D6FC}=2$ there was approximately an 80 % increase in the peak amplitude response compared to that of a non-rotating cylinder. The observed amplitude response measured over the Reynolds-number range of (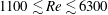 $1100\lesssim Re\lesssim 6300$ ) is significantly different from numerical predictions and other experimental results recorded at significantly lower Reynolds numbers.
$1100\lesssim Re\lesssim 6300$ ) is significantly different from numerical predictions and other experimental results recorded at significantly lower Reynolds numbers.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 80
- Cited by


