Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-03T01:49:41.832Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental observation of hairpin auto-generation events in a turbulent boundary layer

Published online by Cambridge University Press:  19 April 2016

Y. Jodai  and
G. E. Elsinga
Y. Jodai
Affiliation:
Department of Mechanical Engineering, National Institute of Technology, Kagawa College, Takamatsu, 7618058, Japan
G. E. Elsinga*
Affiliation:
Laboratory for Aero and Hydrodynamics, Delft University of Technology, 2628 CA Delft, The Netherlands
*
†Email address for correspondence: g.e.elsinga@tudelft.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

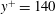Time-resolved tomographic particle image velocimetry experiments show that new hairpin vortices are generated within a fully developed and unperturbed turbulent boundary layer. The measurements are taken at a Reynolds number based on the momentum thickness of 2038, and cover the near-wall region below $y^{+}=140$, where 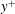$y^{+}$ is the wall-normal distance in wall units. Instantaneous visualizations of the flow reveal near-wall low-speed streaks with associated quasi-streamwise vortices, retrograde inverted arch vortices, hairpin vortices and hairpin packets. The hairpin heads are observed as close to the wall as 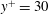$y^{+}=30$. Examples of hairpin packet evolution reveal the development of new hairpin vortices, which are created upstream and close to the wall in a manner consistent with the auto-generation model (Zhou et al., J. Fluid Mech., vol. 387, 1999, pp. 353–396). The development of the new hairpin appears to be initiated by an approaching sweep event, which perturbs the shear layer associated with the initial packet. The shear layer rolls up, thereby forming the new hairpin head. The head subsequently connects to existing streamwise vortices and develops into a hairpin. The time scale associated with the hairpin auto-generation is 20–30 wall units of time. This demonstrates that hairpins can be created over short distances within a developed turbulent boundary layer, implying that they are not simply remnants of the laminar-to-turbulent transition process far upstream.

JFM classification

Boundary Layers: Boundary Layers Boundary Layers: Boundary layer structure
Type
Papers
Information
Journal of Fluid Mechanics , Volume 795 , 25 May 2016 , pp. 611 - 633
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Casey, T. A., Sakakibara, J. & Thoroddsen, S. T. 2013 Scanning tomographic particle image velocimetry applied to a turbulent jet. Phys. Fluids 25, 025102.CrossRefGoogle Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.CrossRefGoogle Scholar
Del Alamo, J. C. & Jimenez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
Discetti, S., Natale, A. & Astarita, T. 2013 Spatial filtering improved tomographic PIV. Exp. Fluids 54, 1–13.CrossRefGoogle Scholar
Eisma, J., Westerweel, J., Ooms, G. & Elsinga, G. E. 2015 Interfaces and internal layers in a turbulent boundary layer. Phys. Fluids 27, 055103.CrossRefGoogle Scholar
Elsinga, G. E., Adrian, R. J., Van Oudheusden, B. W. & Scarano, F. 2010 Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer. J. Fluid Mech. 644, 35–60.CrossRefGoogle Scholar
Elsinga, G. E., Kuik, D. J., Van Oudheusden, B. W. & Scarano, F. 2007 Investigation of the three-dimensional coherent structures in a turbulent boundary layer. In Forty-fifth AIAA Aerospace Sciences Meeting, Reno, NV, AIAA Paper-2007-1305.Google Scholar
Elsinga, G. E., Scarano, F., Wieneke, B. & Van Oudheusden, B. W. 2006 Tomographic particle image velocimetry. Exp. Fluids 41, 933–947.CrossRefGoogle Scholar
Elsinga, G. E. & Westerweel, J. 2012 Tomographic-PIV measurement of the flow around a zigzag boundary layer trip. Exp. Fluids 52, 865–876.CrossRefGoogle Scholar
Elsinga, G. E., Westerweel, J., Scarano, F. & Novara, M. 2011 On the velocity of ghost particles and the bias errors in tomographic-PIV. Exp. Fluids 50, 825–838.CrossRefGoogle Scholar
Erm, L. P. & Joubert, P. N. 1991 Low-Reynolds-number turbulent boundary layers. J. Fluid Mech. 230, 1–44.CrossRefGoogle Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2007 Determination of complete velocity gradient tensor by using cinematographic stereoscopic PIV in a turbulent jet. Exp. Fluids 42, 923–939.CrossRefGoogle Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.CrossRefGoogle Scholar
Gao, Q., Ortiz-Dueñas, C. & Longmire, E. K. 2013 Evolution of coherent structures in turbulent boundary layers based on moving tomographic PIV. Exp. Fluids 54, 1–16.CrossRefGoogle Scholar
Ghaemi, S. & Scarano, F. 2013 Turbulent structure of high-amplitude pressure peaks within the turbulent boundary layer. J. Fluid Mech. 735, 381–426.CrossRefGoogle Scholar
Goudar, M. V., Breugem, W. P. & Elsinga, G. E. 2016 Auto-generation in wall turbulence by the interaction of weak eddies. Phys. Fluids (in press).CrossRefGoogle Scholar
Gupta, A. K., Laufer, J. & Kaplan, R. E. 1971 Spatial structure in the viscous sublayer. J. Fluid Mech. 50, 493–512.CrossRefGoogle Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Herpin, S., Stanislas, M., Foucaut, J. M. & Coudert, S. 2013 Influence of the Reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.CrossRefGoogle Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.CrossRefGoogle Scholar
Jimenez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.CrossRefGoogle Scholar
Jimenez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Jimenez, J. & Simens, M. P. 2001 Low-dimensional dynamics of a turbulent wall flow. J. Fluid Mech. 435, 81–91.CrossRefGoogle Scholar
Jimenez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
Kähler, C. J.2004 The significance of coherent flow structures for the turbulent mixing in wall-bounded flows. Dissertation, DLR Forschungsbericht 2004-24.Google Scholar
Kähler, C. J., Scharnowski, S. & Cierpka, C. 2012 On the uncertainty of digital PIV and PTV near walls. Exp. Fluids 52, 1641–1656.CrossRefGoogle Scholar
Kim, K., Sung, H. J. & Adrian, R. J. 2008 Effects of background noise on generating coherent packets of hairpin vortices. Phys. Fluids 20, 105107.CrossRefGoogle Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.CrossRefGoogle Scholar
Lawson, J. M. & Dawson, J. R. 2014 A scanning PIV method for fine-scale turbulence measurements. Exp. Fluids 55, 1–19.CrossRefGoogle Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13, 735.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3,1–11.CrossRefGoogle Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.CrossRefGoogle Scholar
Saikrishnan, N., Marusic, I. & Longmire, E. 2006 Assessment of dual plane PIV measurements in wall turbulence using DNS data. Exp. Fluids 41, 265–278.CrossRefGoogle Scholar
Savitzky, A. & Golay, M. J. E. 1964 Smoothing and differentiation of data by simplified least squares procedures. Analyt. Chem. 36, 1627–1639.CrossRefGoogle Scholar
Scarano, F. & Riethmuller, M. L. 2000 Advances in iterative multigrid PIV image processing. Exp. Fluids 29, S51–S60.CrossRefGoogle Scholar
Schlatter, P., Brandt, L., de Lange, H. C. & Henningson, D. S. 2008 On streak breakdown in bypass transition. Phys. Fluids 20, 101505.CrossRefGoogle Scholar
Schlatter, P., Li, Q., Örlü, R., Hussain, F. & Henningson, D. S. 2014 On the near-wall vortical structures at moderate Reynolds numbers. Eur. J. Mech. (B/Fluids) 48, 75–93.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2012 Turbulent boundary layers at moderate Reynolds numbers: inflow length and tripping effects. J. Fluid Mech. 710, 5–34.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
Schröder, A., Geisler, R., Elsinga, G. E., Scarano, F. & Dierksheide, U. 2008 Investigation of a turbulent spot and a tripped turbulent boundary layer flow using time-resolved tomographic PIV. Exp. Fluids 44, 305–316.CrossRefGoogle Scholar
Schröder, A., Geisler, R., Staack, K., Elsinga, G. E., Scarano, F., Wieneke, B., Henning, A., Poelma, C. & Westerweel, J. 2011 Eulerian and Lagrangian views of a turbulent boundary layer flow using time-resolved tomographic PIV. Exp. Fluids 50, 1071–1091.CrossRefGoogle Scholar
Sheng, J., Malkiel, E. & Katz, J. 2009 Buffer layer structures associated with extreme wall stress events in a smooth wall turbulent boundary layer. J. Fluid Mech. 633, 17–60.CrossRefGoogle Scholar
Smith, C. R. 1984 Asynthesized model of the near-wall behavior in turbulent boundary layers. In Proceedings of 8th Biennial Symposium on Turbulence (ed. Zakin, J. L. & Patterson, G.), University of Missouri–Rolla.Google Scholar
Smith, C. R. & Metzler, S. P. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.CrossRefGoogle Scholar
Smith, C. R., Walker, J. D. A., Haidari, A. H. & Sobrun, U. 1991 On the dynamics of near-wall turbulence. Phil. Trans. R. Soc. Lond. A 336, 131–175.Google Scholar
Stanislas, M., Perret, L. & Foucaut, J. 2008 Vortical structures in the turbulent boundary layer: a possible route to a universal representation. J. Fluid Mech. 602, 327–382.CrossRefGoogle Scholar
Tanahashi, M., Kang, S. J., Miyamoto, T., Shiokawa, S. & Miyauchi, T. 2004 Scaling law of fine scale eddies in turbulent channel flows up to Re 𝜏 = 800. Intl J. Heat Fluid Flow 25, 331–340.CrossRefGoogle Scholar
Theodorsen, T. 1952 Mechanism of turbulence. In Proceedings of the Midwestern Conference on Fluid Mechanics, Ohio State University, Columbus, OH.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.CrossRefGoogle Scholar
Westerweel, J., Elsinga, G. E. & Adrian, R. J. 2013 Particle image velocimetry for complex and turbulent flows. Annu. Rev. Fluid Mech. 45, 409–436.CrossRefGoogle Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39, 1096–1100.CrossRefGoogle Scholar
Wieneke, B. 2008 Volume self-calibration for 3D particle image velocimetry. Exp. Fluids 45, 549–556.CrossRefGoogle Scholar
Wu, X. 2010 Establishing the generality of three phenomena using a boundary layer with free-stream passing wakes. J. Fluid Mech. 664, 193–219.CrossRefGoogle Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.CrossRefGoogle Scholar
Wu, Y. & Christensen, K. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.CrossRefGoogle Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar

Jodai and Elsinga supplementary movie

Figure 10

Download Jodai and Elsinga supplementary movie(Video)
Video 23 MB

Jodai and Elsinga supplementary movie

Figure 12

Download Jodai and Elsinga supplementary movie(Video)
Video 12.6 MB