Article contents
Extreme events and non-Kolmogorov 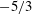 $-5/3$ spectra in turbulent flows behind two side-by-side square cylinders
$-5/3$ spectra in turbulent flows behind two side-by-side square cylinders
Published online by Cambridge University Press: 12 July 2019
Abstract
Turbulent flows behind two side-by-side square cylinders with three different gap ratios, namely, 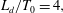 $L_{d}/T_{0}=4,$ 6 and 8 (
$L_{d}/T_{0}=4,$ 6 and 8 (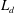 $L_{d}$ is the separation distance between two cylinders and
$L_{d}$ is the separation distance between two cylinders and 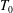 $T_{0}$ is the cylinder thickness) are investigated by using direct numerical simulations. Depending on the strength of the gap flow, the three cases can generally be characterized into two regimes, one being the weak gap flow regime and the other being the robust gap flow regime. The wake-interaction length scale can only be applied to characterize the spatial evolution of the dual-wake flow in the robust gap flow regime. And only in this regime can the so-called ‘extreme events’ (i.e. non-Gaussian velocity fluctuations with large flatness) be identified. For the case with
$T_{0}$ is the cylinder thickness) are investigated by using direct numerical simulations. Depending on the strength of the gap flow, the three cases can generally be characterized into two regimes, one being the weak gap flow regime and the other being the robust gap flow regime. The wake-interaction length scale can only be applied to characterize the spatial evolution of the dual-wake flow in the robust gap flow regime. And only in this regime can the so-called ‘extreme events’ (i.e. non-Gaussian velocity fluctuations with large flatness) be identified. For the case with 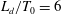 $L_{d}/T_{0}=6$, two downstream locations, i.e.
$L_{d}/T_{0}=6$, two downstream locations, i.e. 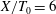 $X/T_{0}=6$ and 26, at which the turbulent flows are highly non-Gaussian distributed and approximately Gaussian distributed, respectively, are analysed in detail. A well-defined
$X/T_{0}=6$ and 26, at which the turbulent flows are highly non-Gaussian distributed and approximately Gaussian distributed, respectively, are analysed in detail. A well-defined 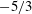 $-5/3$ energy spectrum can be found in the near-field region (i.e.
$-5/3$ energy spectrum can be found in the near-field region (i.e. 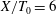 $X/T_{0}=6$), where the turbulent flow is still developing and highly intermittent and Kolmogorov’s universal equilibrium hypothesis does not hold. We confirm that the approximate
$X/T_{0}=6$), where the turbulent flow is still developing and highly intermittent and Kolmogorov’s universal equilibrium hypothesis does not hold. We confirm that the approximate 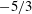 $-5/3$ power law in the high-frequency range is closely related to the occurrences of the extreme events. As the downstream distance increases, the velocity fluctuations gradually adopt a Gaussian distribution, corresponding to a decrease in the strength of the extreme events. Consequently, the range of the
$-5/3$ power law in the high-frequency range is closely related to the occurrences of the extreme events. As the downstream distance increases, the velocity fluctuations gradually adopt a Gaussian distribution, corresponding to a decrease in the strength of the extreme events. Consequently, the range of the 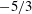 $-5/3$ power law narrows. In the upstream region (i.e.
$-5/3$ power law narrows. In the upstream region (i.e. 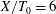 $X/T_{0}=6$), the second-order structure function exhibits a power-law exponent close to
$X/T_{0}=6$), the second-order structure function exhibits a power-law exponent close to  $1$, whereas in the far downstream region (i.e.
$1$, whereas in the far downstream region (i.e. 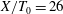 $X/T_{0}=26$) the expected
$X/T_{0}=26$) the expected 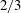 $2/3$ power-law exponent appears. The larger exponent at
$2/3$ power-law exponent appears. The larger exponent at 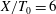 $X/T_{0}=6$ is related to the fact that fluid motions in the intermediate range can directly ‘feel’ the large-scale vortex shedding.
$X/T_{0}=6$ is related to the fact that fluid motions in the intermediate range can directly ‘feel’ the large-scale vortex shedding.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 17
- Cited by


