Hostname: page-component-84b7d79bbc-g78kv Total loading time: 0 Render date: 2024-07-25T16:19:10.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Force-induced diffusion in suspensions of hydrodynamically interacting colloids

Published online by Cambridge University Press:  20 April 2016

N. J. Hoh  and
R. N. Zia
N. J. Hoh
Affiliation:
School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14850, USA
R. N. Zia*
Affiliation:
School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14850, USA
*
†Email address for correspondence: zia@cbe.cornell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the influence of hydrodynamic, thermodynamic and interparticle forces on the diffusive motion of a Brownian probe driven by a constant external force through a dilute colloidal dispersion. The influence of these microscopic forces on equilibrium self-diffusivity (passive microrheology) is well known: all three act to hinder the short- and long-time self-diffusion. Here, via pair-Smoluchowski theory, we explore their influence on self-diffusion in a flowing suspension, where particles and fluid have been set into motion by an externally forced probe (active microrheology), giving rise to non-equilibrium flow-induced diffusion. The probe’s motion entrains background particles as it travels through the bath, deforming the equilibrium suspension microstructure. The shape and extent of microstructural distortion is set by the relative strength of the external force 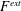$F^{\mathit{ext}}$ to the entropic restoring force 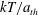$kT/a_{\mathit{th}}$ of the bath particles, defining a Péclet number 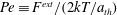$\mathit{Pe}\equiv F^{\mathit{ext}}/(2kT/a_{\mathit{th}})$; and also by the strength of hydrodynamic interactions, set by the range of interparticle repulsion 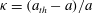${\it\kappa}=(a_{\mathit{th}}-a)/a$, where 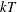$kT$ is the thermal energy and 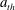$a_{\mathit{th}}$ and $a$ are the thermodynamic and hydrodynamic sizes of the particles, respectively. We find that in the presence of flow, the same forces that hinder equilibrium diffusion now enhance it, with diffusive anisotropy set by the range of interparticle repulsion ${\it\kappa}$. A transition from hindered to enhanced diffusion occurs when diffusive and advective forces balance, 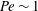$\mathit{Pe}\sim 1$, where the exact value is a sensitive function of the strength of hydrodynamics, ${\it\kappa}$. We find that the hindered to enhanced transition straddles two transport regimes: in hindered diffusion, stochastic forces in the presence of other bath particles produce deterministic displacements (Brownian drift) at the expense of a maximal random walk. In enhanced diffusion, driving the probe with a deterministic force through an initially random suspension leads to fluctuations in the duration of probe–bath particle entrainment, giving rise to enhanced, flow-induced diffusion. The force-induced diffusion is anisotropic for all 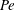$\mathit{Pe}$, scaling as 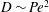$D\sim \mathit{Pe}^{2}$ in all directions for weak forcing, regardless of the strength of hydrodynamic interactions. When probe forcing is strong, 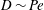$D\sim \mathit{Pe}$ in all directions in the absence of hydrodynamic interactions, but the picture changes qualitatively as hydrodynamic interactions grow strong. In this nonlinear regime, microstructural asymmetry weakens while the anisotropy of the force-induced diffusion tensor increases dramatically. This behaviour owes its origins to the approach toward Stokes flow reversibility, where diffusion along the direction of probe force scales advectively while transverse diffusion must vanish.

JFM classification

Complex Fluids: Colloids Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 795 , 25 May 2016 , pp. 739 - 783
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbott, J. R., Graham, A. L., Mondy, L. A. & Brenner, H. 1998 Dispersion of a ball settling through a quiescent neutrally buoyant suspension. J. Fluid Mech. 361, 309–331.Google Scholar
Acrivos, A., Batchelor, G. K., Hinch, E. J., Koch, D. L. & Mauri, R. 1992 Longitudinal shear-induced diffusion of spheres in a dilute suspension. J. Fluid Mech. 240, 651–657.Google Scholar
Acrivos, A., Mauri, R. & Fan, X. 1993 Shear-induced resuspension in a Couette device. Intl J. Multiphase Flow 19, 797–802.Google Scholar
Almog, Y. & Brenner, H. 1997 Non-continuum anomalies in the apparent viscosity experienced by a test sphere moving through an otherwise quiescent suspension. Phys. Fluids 9 (1), 16–22.Google Scholar
Arp, P. A. & Mason, S. G. 1977 The kinetics of flowing dispersions. IX. Doublets of rigid spheres. J. Colloid Interface Sci. 61, 44–61.Google Scholar
Batchelor, G. K. 1972 Sedimentation in a dilute dispersion of spheres. J. Fluid Mech. 52 (2), 245–268.Google Scholar
Batchelor, G. K. 1976 Brownian diffusion of particles with hydrodynamic interaction. J. Fluid Mech. 74, 1–29.CrossRefGoogle Scholar
Batchelor, G. K. 1982 Sedimentation in a dilute polydisperse system of interacting spheres. Part 1. General theory. J. Fluid Mech. 119, 379–407.Google Scholar
Batchelor, G. K. 1983 Diffusion in a dilute polydisperse system of interacting spheres. J. Fluid Mech. 131, 155–175.Google Scholar
Batchelor, G. K. & Green, J. T. 1972 The hydrodynamic interaction of two small freely-moving spheres in a linear flow field. J. Fluid Mech. 56 (2), 375–400.CrossRefGoogle Scholar
Batchelor, G. K. & Wen, C.-S. 1982 Sedimentation in a dilute polydisperse system of interacting spheres. Part 2. Numerical results. J. Fluid Mech. 124, 495–528.Google Scholar
Bergenholtz, J., Brady, J. F. & Vicic, M. 2002 The non-Newtonian rheology of dilute colloidal suspensions. J. Fluid Mech. 456, 239–275.Google Scholar
Brady, J. F. 1994 The long-time self-diffusivity in concentrated colloidal dispersions. J. Fluid. Mech. 272, 109–133.Google Scholar
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid. Mech. 348, 103–139.CrossRefGoogle Scholar
da Cunha, F. R. & Hinch, E. J. 1996 Shear-induced dispersion in a dilute suspension of rough spheres. J. Fluid Mech. 309, 211–223.Google Scholar
Davis, R. H. 1992 Effects of surface roughness on a sphere sedimenting through a dilute suspension of neutrally buoyant spheres. Phys. Fluids A 4, 2607–2619.CrossRefGoogle Scholar
Davis, R. H. & Hill, N. A. 1992 Hydrodynamic diffusion of a sphere sedimenting through a dilute suspension of neutrally buoyant spheres. J. Fluid Mech. 236, 513–533.Google Scholar
Eckstein, E. C., Bailey, D. G. & Shapiro, A. H. 1977 Self-diffusion of particles in shear flow of a suspension. J. Fluid Mech. 79, 191–208.Google Scholar
Einstein, A. 1906 On the theory of the Brownian movement. Ann. Phys. 19 (4), 371–381.CrossRefGoogle Scholar
Ermak, D. L. & McCammon, J. A. 1978 Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 69, 1352–1360.CrossRefGoogle Scholar
Fåhræus, R. & Lindqvist, T. 1931 The viscosity of the blood in narrow capillary tubes. Am. J. Physiol. 96, 562–568.CrossRefGoogle Scholar
Fixman, M. 1978 Simulation of polymer dynamics. I. General theory. J. Chem. Phys. 69, 1527–1537.Google Scholar
Gadala-Maria, F. & Acrivos, A. 1980 Shear-induced structure in a concentrated suspension of solid spheres. J. Rheol. 24 (6), 799–814.CrossRefGoogle Scholar
Ham, J. M. & Homsy, G. M. 1988 Hindered settling and hydrodynamic dispersion in quiescent sedimenting suspensions. Intl J. Multiphase Flow 14, 533–546.CrossRefGoogle Scholar
Hasimoto, H. 1959 On the periodic fundamental solutions of the Stokes equations and their application to viscous flow past a cubic array of spheres. J. Fluid Mech. 5 (2), 317–328.Google Scholar
Hoh, N. J. & Zia, R. N. 2015 Hydrodynamic diffusion in active microrheology of non-colloidal suspensions: the role of interparticle forces. J. Fluid Mech. 785, 189–218.Google Scholar
Jeffrey, D. J. & Onishi, Y. 1984 Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 139, 261–290.Google Scholar
Khair, A. S. & Brady, J. F. 2006 Single particle motion in colloidal dispersions: a simple model for active and nonlinear microrheology. J. Fluid Mech. 557, 73–117.CrossRefGoogle Scholar
Kim, S. & Karrila, S. J. 1991 Microhydrodynamics: Principles and Selected Applications. Butterworth-Heinemann.Google Scholar
Koch, D. L. & Shaqfeh, E. S. G. 1991 Screening in sedimenting suspensions. J. Fluid Mech. 224, 275–303.Google Scholar
Kops-Werkhoven, M. M. & Fijnaut, H. M. 1982 Dynamic behavior of silica dispersions studied near the optical matching point. J. Chem. Phys. 77, 2242–2253.Google Scholar
Kumar, A., Henríquez Rivera, R. G. & Graham, M. D. 2014 Flow-induced segregation in confined multicomponent suspensions: effects of particle size and rigidity. J. Fluid Mech. 738, 423–462.CrossRefGoogle Scholar
Leighton, D. & Acrivos, A. 1986 Viscous resuspension. Chem. Engng Sci. 41, 1377–1384.Google Scholar
Leighton, D. & Acrivos, A. 1987a Measurement of shear-induced self-diffusion in concentrated suspensions of spheres. J. Fluid Mech. 177, 109–131.Google Scholar
Leighton, D. & Acrivos, A. 1987b The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439.Google Scholar
Lekkerkerker, H. N. W. & Dhont, J. K. G. 1984 On the calculation of the self-diffusion coefficient of interacting Brownian particles. J. Chem. Phys. 80, 5790–5792.Google Scholar
van Megen, W. & Underwood, S. M. 1989 Tracer diffusion in concentrated colloidal dispersions. III. Mean squared displacements and self-diffusion coefficients. J. Chem. Phys. 91 (1), 552–559.Google Scholar
van Megen, W., Underwood, S. M. & Snook, I. 1986 Tracer diffusion in concentrated colloidal dispersions. J. Chem. Phys. 85 (7), 4065–4072.Google Scholar
Morris, J. F. & Brady, J. F. 1996 Self-diffusion in sheared suspensions. J. Fluid. Mech. 312, 223–252.Google Scholar
Nicolai, H., Herzhaft, B., Hinch, E. J., Oger, L. & Guazzelli, E. 1995 Particle velocity fluctuations and hydrodynamic self-diffusion of sedimenting non-Brownian spheres. Phys. Fluids 7, 12–23.CrossRefGoogle Scholar
Nicolai, H., Peysson, Y. & Guazzelli, É. 1996 Velocity fluctuations of a heavy sphere falling through a sedimenting suspension. Phys. Fluids 8, 855–862.Google Scholar
Phillips, R. J., Armstrong, R. C., Brown, R. A., Graham, A. L. & Abbott, J. L. 1992 A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids A 4, 30–40.Google Scholar
Rallison, J. M. & Hinch, E. J. 1986 The effect of particle interactions on dynamic light scattering from a dilute suspension. J. Fluid Mech. 167, 131–168.CrossRefGoogle Scholar
Russel, W. B. 1984 The Huggins coefficient as a means for characterizing suspended particles. J. Chem. Soc. Faraday Trans. 2 80 (1), 31–41.Google Scholar
Squires, T. M. & Brady, J. F. 2005 A simple paradigm for active and nonlinear microrheology. Phys. Fluids 17 (7), 073101.Google Scholar
Stillinger, F. H. & Weber, T. A. 1982 Hidden structure in liquids. Phys. Rev. A 25, 978–989.CrossRefGoogle Scholar
Su, Y., Chu, H. C. W. & Zia, R. N.2015a Microviscosity, normal stress and osmotic pressure of Brownian suspensions by accelerated stokesian dynamics simulation. Unpublished.Google Scholar
Su, Y., Gu, K. L., Hoh, N. J. & Zia, R. N.2015b Force-induced diffusion of Brownian suspensions by accelerated stokesian dynamics simulation. Unpublished.Google Scholar
Swan, J. W. & Zia, R. N. 2013 Active microrheology – fixed-velocity versus fixed-force. Phys. Fluids 25 (8), 083303.Google Scholar
Tangelder, G. J., Teirlinck, H. C., Slaaf, D. W. & Reneman, R. S. 1985 Distribution of blood platelets flowing in arterioles. Am. J. Physiol. Heart Circ. Physiol. 248 (3), H318–H323.CrossRefGoogle ScholarPubMed
Wang, Y., Mauri, R. & Acrivos, A. 1996 The transverse shear-induced liquid and particle tracer diffusivities of a dilute suspension of spheres undergoing a simple shear flow. J. Fluid Mech. 327, 255–272.CrossRefGoogle Scholar
Zhang, K. & Acrivos, A. 1994 Viscous resuspension in fully developed laminar pipe flows. Intl J. Multiphase Flow 20, 579–591.Google Scholar
Zia, R. N. & Brady, J. F. 2010 Single-particle motion in colloids: force-induced diffusion. J. Fluid Mech. 658, 188–210.CrossRefGoogle Scholar
Zia, R. N. & Brady, J. F. 2012 Microviscosity, microdiffusivity, and normal stresses in colloidal dispersions. J. Rheol. 56 (5), 1175–1208.Google Scholar
Zia, R. N. & Brady, J. F. 2013 Stress development, relaxation, and memory in colloidal dispersions: transient nonlinear microrheology. J. Rheol. 57 (2), 457–492.Google Scholar
Zia, R. N., Landrum, B. J. & Russel, W. B. 2014 A micro-mechanical study of coarsening and rheology of colloidal gels: cage building, cage hopping, and Smoluchowski’s ratchet. J. Rheol. 58 (5), 1121–1157.Google Scholar
Zwanzig, R. 1983 On the relation between self-diffusion and viscosity of liquids. J. Chem. Phys. 79, 4507–4508.Google Scholar