Article contents
Free-stream coherent structures in growing boundary layers: a link to near-wall streaks
Published online by Cambridge University Press: 05 August 2015
Abstract
In a recent paper, Deguchi & Hall (J. Fluid Mech., vol. 752, 2014a, pp. 602–625) described a new kind of exact coherent structure which sits at the edge of an asymptotic suction boundary layer at high values of the Reynolds number 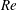 $Re$ . At a distance
$Re$ . At a distance 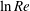 $\ln Re$ from the wall, the structure is driven by the fully nonlinear interaction of tiny rolls, waves and streaks convected downstream at almost the free-stream speed. The interaction problem satisfies the unit-Reynolds-number three-dimensional Navier–Stokes equations and is localized in a layer of the same depth as the unperturbed boundary layer. Here, we show that the interaction problem is generic to any boundary layer that approaches its free-stream form through an exponentially small correction. It is shown that away from the layer where it is generated the induced roll–streak flow is dominated by non-parallel effects which now play a major role in the streamwise evolution of the structure. The similarity with the parallel boundary layer case is restricted only to the layer where it is generated. It is shown that non-parallel effects cause the structure to persist only over intervals of finite length in any growing boundary layer and lead to a flow structure reminiscent of turbulent boundary layer simulations. The results found shed light on a possible mechanism to couple near-wall streaks with coherent structures located towards the edge of a turbulent boundary layer. Some discussion of how the mechanism adapts to a three-dimensional base flow is given.
$\ln Re$ from the wall, the structure is driven by the fully nonlinear interaction of tiny rolls, waves and streaks convected downstream at almost the free-stream speed. The interaction problem satisfies the unit-Reynolds-number three-dimensional Navier–Stokes equations and is localized in a layer of the same depth as the unperturbed boundary layer. Here, we show that the interaction problem is generic to any boundary layer that approaches its free-stream form through an exponentially small correction. It is shown that away from the layer where it is generated the induced roll–streak flow is dominated by non-parallel effects which now play a major role in the streamwise evolution of the structure. The similarity with the parallel boundary layer case is restricted only to the layer where it is generated. It is shown that non-parallel effects cause the structure to persist only over intervals of finite length in any growing boundary layer and lead to a flow structure reminiscent of turbulent boundary layer simulations. The results found shed light on a possible mechanism to couple near-wall streaks with coherent structures located towards the edge of a turbulent boundary layer. Some discussion of how the mechanism adapts to a three-dimensional base flow is given.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 12
- Cited by


