Article contents
Frequency–wavenumber spectral analysis of spatio-temporal flows
Published online by Cambridge University Press: 08 June 2018
Abstract
We propose a fully spatio-temporal approach for identifying spatially varying modes of oscillation in fluid dynamics simulation output by means of multitaper frequency–wavenumber spectral analysis. One-dimensional spectrum estimation has proven to be a valuable tool in the analysis of turbulence data applied spatially to determine the rate of energy transport between spatial scales, or temporally to determine frequencies of oscillatory flows. It also allows for the quantitative comparison of flow characteristics between two scenarios using a standard basis. It has the limitation, however, that it neglects coupling between spatial and temporal structures. Two-dimensional frequency–wavenumber spectral analysis allows one to decompose waveforms into standing or travelling variety. The extended higher-dimensional multitaper method proposed here is shown to have improved statistical properties over conventional non-parametric spectral estimators, and is accompanied by confidence intervals which estimate their uncertainty. Multitaper frequency–wavenumber analysis is applied to a canonical benchmark problem, namely, a direct numerical simulation of von Kármán vortex shedding off a square wall-mounted cylinder with two inflow scenarios with matching momentum-thickness Reynolds numbers 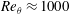 $Re_{\unicode[STIX]{x1D703}}\approx 1000$ at the obstacle. Frequency–wavenumber analysis of a two-dimensional section of these data reveals that although both the laminar and turbulent inflow scenarios show a turbulent
$Re_{\unicode[STIX]{x1D703}}\approx 1000$ at the obstacle. Frequency–wavenumber analysis of a two-dimensional section of these data reveals that although both the laminar and turbulent inflow scenarios show a turbulent 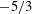 $-5/3$ cascade in wavenumber (
$-5/3$ cascade in wavenumber ( $\unicode[STIX]{x1D708}$ ) and frequency (
$\unicode[STIX]{x1D708}$ ) and frequency (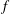 $f$ ), the flow characteristics differ in that there is a significantly more prominent discrete harmonic oscillation near
$f$ ), the flow characteristics differ in that there is a significantly more prominent discrete harmonic oscillation near 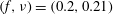 $(f,\unicode[STIX]{x1D708})=(0.2,0.21)$ in wavenumber and frequency in the laminar inflow scenario than the turbulent scenario. This frequency–wavenumber pair corresponds to a travelling wave with velocity near one near the centre path of the vortex street.
$(f,\unicode[STIX]{x1D708})=(0.2,0.21)$ in wavenumber and frequency in the laminar inflow scenario than the turbulent scenario. This frequency–wavenumber pair corresponds to a travelling wave with velocity near one near the centre path of the vortex street.
Information
- Type
- JFM Papers
- Information
- Copyright
- © Cambridge University Press 2018. This is a work of the U.S. Government and is not subject to copyright protection in the United States.
References
- 12
- Cited by


