Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
ONOMURA, Shiho
HATTORI, Yasuo
INAGAKI, Atsushi
TAKIMOTO, Hiroshi
and
KANDA, Manabu
2011.
INVESTIGATION OF THERMAL BOUNDARY LAYER ALONG THE VERTICAL WALL OF A BUILDING.
Journal of Japan Society of Civil Engineers, Ser. B1 (Hydraulic Engineering),
Vol. 67,
Issue. 4,
p.
I_337.
Jenkins, Adrian
2011.
Convection-Driven Melting near the Grounding Lines of Ice Shelves and Tidewater Glaciers.
Journal of Physical Oceanography,
Vol. 41,
Issue. 12,
p.
2279.
Xu, Xiao Ping
2011.
New algebraic approaches to classical boundary layer problems.
Acta Mathematica Sinica, English Series,
Vol. 27,
Issue. 6,
p.
1023.
Sciascia, R.
Straneo, F.
Cenedese, C.
and
Heimbach, P.
2013.
Seasonal variability of submarine melt rate and circulation in an East Greenland fjord.
Journal of Geophysical Research: Oceans,
Vol. 118,
Issue. 5,
p.
2492.
Garel, F.
Kaminski, E.
Tait, S.
and
Limare, A.
2013.
The influence of wind on the estimation of lava effusion rate from thermal remote-sensing.
Journal of Volcanology and Geothermal Research,
Vol. 264,
Issue. ,
p.
223.
Hajra, Bodhisatta
2014.
A Review of Some Recent Studies on Buoyancy Driven Flows in an Urban Environment.
International Journal of Atmospheric Sciences,
Vol. 2014,
Issue. ,
p.
1.
Beaird, Nicholas
Straneo, Fiammetta
and
Jenkins, William
2015.
Spreading of Greenland meltwaters in the ocean revealed by noble gases.
Geophysical Research Letters,
Vol. 42,
Issue. 18,
p.
7705.
Cowton, Tom
Slater, Donald
Sole, Andrew
Goldberg, Dan
and
Nienow, Peter
2015.
Modeling the impact of glacial runoff on fjord circulation and submarine melt rate using a new subgrid‐scale parameterization for glacial plumes.
Journal of Geophysical Research: Oceans,
Vol. 120,
Issue. 2,
p.
796.
Kerr, Ross C.
and
McConnochie, Craig D.
2015.
Dissolution of a vertical solid surface by turbulent compositional convection.
Journal of Fluid Mechanics,
Vol. 765,
Issue. ,
p.
211.
Gayen, Bishakhdatta
Griffiths, Ross W.
and
Kerr, Ross C.
2016.
Simulation of convection at a vertical ice face dissolving into saline water.
Journal of Fluid Mechanics,
Vol. 798,
Issue. ,
p.
284.
Fan, Yifan
Li, Yuguo
Hang, Jian
Wang, Kai
and
Yang, Xinyan
2016.
Natural convection flows along a 16-storey high-rise building.
Building and Environment,
Vol. 107,
Issue. ,
p.
215.
Caudwell, T.
Flór, J.-B.
and
Negretti, M. E.
2016.
Convection at an isothermal wall in an enclosure and establishment of stratification.
Journal of Fluid Mechanics,
Vol. 799,
Issue. ,
p.
448.
Slater, Donald A.
Goldberg, Dan N.
Nienow, Peter W.
and
Cowton, Tom R.
2016.
Scalings for Submarine Melting at Tidewater Glaciers from Buoyant Plume Theory.
Journal of Physical Oceanography,
Vol. 46,
Issue. 6,
p.
1839.
McConnochie, Craig D.
and
Kerr, Ross C.
2016.
The turbulent wall plume from a vertically distributed source of buoyancy.
Journal of Fluid Mechanics,
Vol. 787,
Issue. ,
p.
237.
Magorrian, Samuel J.
and
Wells, Andrew J.
2016.
Turbulent plumes from a glacier terminus melting in a stratified ocean.
Journal of Geophysical Research: Oceans,
Vol. 121,
Issue. 7,
p.
4670.
Hogg, Charlie A. R.
Dalziel, Stuart B.
Huppert, Herbert E.
and
Imberger, Jörg
2017.
Inclined gravity currents filling basins: the impact of peeling detrainment on transport and vertical structure.
Journal of Fluid Mechanics,
Vol. 820,
Issue. ,
p.
400.
McConnochie, Craig D.
and
Kerr, Ross C.
2017.
Enhanced ablation of a vertical ice wall due to an external freshwater plume.
Journal of Fluid Mechanics,
Vol. 810,
Issue. ,
p.
429.
Fan, Yifan
Li, Yuguo
Hang, Jian
and
Wang, Kai
2017.
Diurnal variation of natural convective wall flows and the resulting air change rate in a homogeneous urban canopy layer.
Energy and Buildings,
Vol. 153,
Issue. ,
p.
201.
Nakao, Keisuke
Hattori, Yasuo
and
Suto, Hitoshi
2017.
Numerical investigation of a spatially developing turbulent natural convection boundary layer along a vertical heated plate.
International Journal of Heat and Fluid Flow,
Vol. 63,
Issue. ,
p.
128.
Yin, Shi
Sandberg, Mats
Lam, Kit-ming
and
Li, Yuguo
2017.
Near-field merging and penetration of triple starting plumes from volumetric heat sources in a calm environment.
International Journal of Heat and Mass Transfer,
Vol. 115,
Issue. ,
p.
1321.
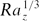 ). This gives a constant heat flux, consistent with previous experimental and theoretical studies. On larger geophysical scales the buoyancy is strongest in the outer layer and the laminar layer is driven by the shear imposed on it. The predicted heat transfer correlation then has the Nusselt number proportional to the one-half power of Rayleigh number (Nu ∝
). This gives a constant heat flux, consistent with previous experimental and theoretical studies. On larger geophysical scales the buoyancy is strongest in the outer layer and the laminar layer is driven by the shear imposed on it. The predicted heat transfer correlation then has the Nusselt number proportional to the one-half power of Rayleigh number (Nu ∝ 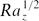 ) so that a larger heat flux is predicted than might be expected from an extrapolation of laboratory-scale results. The criteria for transitions between flow regimes are consistent with a hierarchy of instabilities of the near-wall laminar flow, with a buoyancy-driven instability operating on the laboratory scale and a shear-driven instability operating on geophysical scales.
) so that a larger heat flux is predicted than might be expected from an extrapolation of laboratory-scale results. The criteria for transitions between flow regimes are consistent with a hierarchy of instabilities of the near-wall laminar flow, with a buoyancy-driven instability operating on the laboratory scale and a shear-driven instability operating on geophysical scales.
